Содержание
- 2. Предварительные сведения
- 3. Позиции окончаний endpos, Рассмотрим любую непустую подстроку t строки s. Тогда назовём множеством окончаний endpos(t) множество
- 4. endpos –эквивалентные строки Назовем две подстроки t1 и t2 endpos -эквивалентными, если их множества окончаний совпадают:
- 5. endpos –эквивалентные строки В суффиксном автомате -эквивалентным подстрокам соответствует одно и то же состояние. Число состояний
- 6. endpos –эквивалентные строки Каждому состоянию суффиксного автомата соответствуют одна или несколько подстрок, имеющих одно и то
- 7. endpos –эквивалентные строки. Дополнительные замечания Лемма 1. Две непустые подстроки u и w (length(u)≤ length(w)) являются
- 8. Дополнительные замечания Лемма 2. Рассмотрим две непустые подстроки u и w ( (length(u)≤ length(w)) ). Тогда
- 9. Доказательство леммы 2 Пусть множества endpos(u) и endpos (w) имеют хотя бы один общий элемент. Это
- 10. Дополнительные замечания Лемма 3. Рассмотрим некоторый класс endpos -эквивалентности. Отсортируем все подстроки, входящие в этот класс,
- 11. Доказательство леммы 3(1) Зафиксируем некоторый класс endpos -эквивалентности. Если он содержит только одну строку, то корректность
- 12. Доказательство леммы 3(2) Обозначим через w длиннейшую, а через u— кратчайшую строку в данном классе эквивалентности.
- 13. Суффиксные ссылки Рассмотрим некоторое состояние автомата v≠t0. Cостоянию v соответствует некоторый класс строк с одинаковыми значениями
- 14. Суффиксные ссылки Иными словами, суффиксная ссылка link(v) ведёт в такое состояние, которому соответствует наидлиннейший суффикс строки
- 15. Суффиксные ссылки Лемма 4. Суффиксные ссылки образуют дерево, корнем которого является начальное состояние t0 . Доказательство.
- 16. Суффиксные ссылки Лемма 5. Построим из всех имеющихся множеств endpos дерево (по принципу "множество-родитель содержит как
- 17. Лемма 5(продолжение) Рассмотрим теперь произвольное состояние v≠t0 и его суффиксную ссылку link(v). Из определения суффиксной ссылки
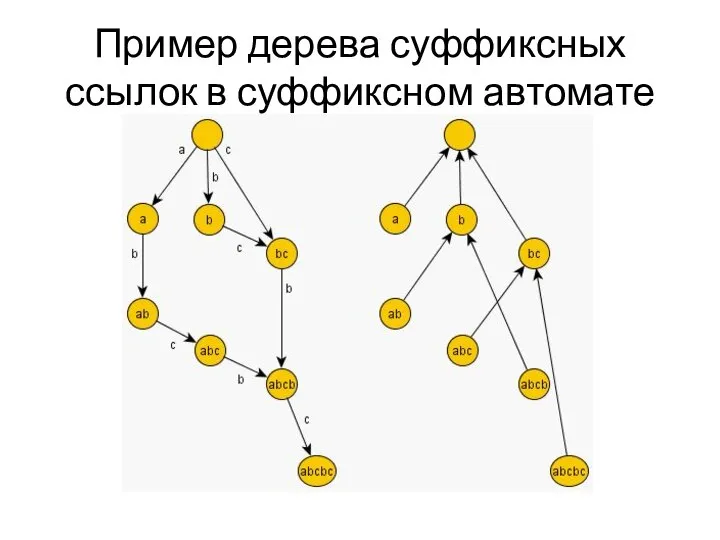
- 18. Пример дерева суффиксных ссылок в суффиксном автомате
- 19. Предварительные итоги-1 Множество подстрок строки s можно разбить на классы эквивалентности согласно их множествам окончания endpos.
- 20. Предварительные итоги-2 Тогда все строки, соответствующие этому состоянию, являются различными суффиксами строки longest(v) и имеют всевозможные
- 21. Предварительные итоги-3 Таким образом, minlen(v) для v≠t0 выражается с помощью суффиксной ссылки link(v) как: minlen(v)≡ len(link(v))+1.
- 22. Алгоритм построения суффиксного автомата за линейное время
- 23. Алгоритм онлайновый, т.е. будет добавлять по одному символу строки s , перестраивая соответствующим образом текущий автомат.
- 24. Предварительные сведения Изначально автомат состоит из единственного состояния t0 , которое условимся считать нулевым состоянием (остальные
- 25. Рассмотрим реализацию обработки добавления 1 символа в конец текущей строки
- 26. Пусть last— это состояние, соответствующее всей текущей строке до добавления символа c. (Изначально last=0, а после
- 27. Сделаем такой цикл: изначально мы стоим в состоянии last; если из него нет перехода по букве
- 28. Если ни разу не случилось, что переход по букве c уже имелся, и мы так и
- 29. Рассмотрим 2 случая Разделяются по выполнению или нет условия len(p)+1 = len(q). Если len(p)+1 = len(q)
- 30. После клонирования мы проводим суффиксную ссылку из cur в это состояние clone, также перенаправляем суффиксную ссылку
- 31. Терминальные вершины Если нужно знать, какие вершины являются терминальными, а какие — нет, то можно найти
- 32. Замечания Отметим, что добавление одного символа приводит к добавлению одного или двух состояний в автомат. Таким
- 33. Доказательство корректности алгоритма Назовём переход (p,q) сплошным, если len(p)+1 = len(q). В противном случае, т.е. когда
- 34. Доказательство корректности алгоритма-пр1 Во избежание неоднозначностей, под строкой s мы будем подразумевать строку, для которой был
- 35. Доказательство корректности алгоритма-пр2 После создания нового состояния алгоритм проходится по суффиксным ссылкам, начиная с состояния, соответствующего
- 36. Доказательство корректности алгоритма-пр3 Самый простой случай — если так и доходим до фиктивного состояния -1 ,
- 37. Доказательство корректности алгоритма-пр4 Второй случай — когда мы наткнулись на уже имеющийся переход (p,q) . Это
- 38. Доказательство корректности алгоритма-пр5 Возникает сложность с тем, куда вести суффиксную ссылку из состояния cur. требуется провести
- 39. Доказательство корректности алгоритма-пр6 Итак, по одному из возможных сценариев, переход (p,q) оказался сплошным, т.е. len(q)=len(p)+1 .
- 40. Доказательство корректности алгоритма-пр7 Более сложный вариант — когда переход несплошной, т.е. len(q)>len(p)+1 . Это означает, что
- 41. Доказательство корректности алгоритма-пр8 Как производить это расщепление? “Kлонируем" состояние q , делая его копию clone с
- 42. Доказательство корректности алгоритма-пр9 Остался последний шаг — перенаправить некоторые входящие в q переходы, перенаправив их на
- 43. Доказательство линейного числа операций Cписок переходов из одной вершины надо хранить в виде сбалансированного дерева, позволяющего
- 44. Доказательство линейного числа операций-пр1 Oперации поиска перехода по символу, добавления перехода, поиск следующего перехода —считаются работающими
- 45. Доказательство линейного числа операций-пр2 Если мы рассмотрим все части алгоритма, то он содержит три части, линейная
- 46. Доказательство линейного числа операций-пр3 Воспользуемся известным фактом, что размер суффиксного автомата (как по числу состояний, так
- 47. Доказательство линейного числа операций-пр4 Тогда очевидна линейная суммарная асимптотика первой и второй частей: ведь каждая операция
- 48. Доказательство линейного числа операций-пр5 Обозначим v=longest(p). Это суффикс строки s , и с каждой итерацией его
- 49. Доказательство линейного числа операций-пр6 Таким образом, каждая итерация этого цикла приводит к тому, что позиция строки
- 51. Скачать презентацию















































 Применение реверс-инжиниринга в медицинской промышленности
Применение реверс-инжиниринга в медицинской промышленности Радиолокация. Классификация и виды
Радиолокация. Классификация и виды Такая нелюбимая. Весёлая Грамматика НЕТРАДИЦИОННЫЙ УРОК-ПРЕЗЕНТАЦИЯ, УРОК - ИГРА. ИЛЬИНА Л.Н.учитель начал
Такая нелюбимая. Весёлая Грамматика НЕТРАДИЦИОННЫЙ УРОК-ПРЕЗЕНТАЦИЯ, УРОК - ИГРА. ИЛЬИНА Л.Н.учитель начал Системы впрыска бензина
Системы впрыска бензина Аппаратная часть компьютерной системы. Схема простого компьютера
Аппаратная часть компьютерной системы. Схема простого компьютера Транспортные задачи
Транспортные задачи Рубежная расчетно-графическая работа по системам компьютерной графики
Рубежная расчетно-графическая работа по системам компьютерной графики  Теория государства и права
Теория государства и права Паспорт комнатных растений
Паспорт комнатных растений  Тяжелая атлетика
Тяжелая атлетика Биоадаптивная оболочка здания
Биоадаптивная оболочка здания Следствия из преобразований Лоренца
Следствия из преобразований Лоренца Дохристианский период восточнославянской культуры. Язычество. Бытовая культура. Обряды.
Дохристианский период восточнославянской культуры. Язычество. Бытовая культура. Обряды. В чем сходство и отличие глиняной игрушки разных ремесленных центров
В чем сходство и отличие глиняной игрушки разных ремесленных центров Аттестационная работа. Тайна исторической народной песни
Аттестационная работа. Тайна исторической народной песни Особенности реализации программы повышения квалификации «Развитие малого бизнеса» в российских образовательных учреждениях
Особенности реализации программы повышения квалификации «Развитие малого бизнеса» в российских образовательных учреждениях  Презентация Культурные ценности, нормы, традиции и инновации
Презентация Культурные ценности, нормы, традиции и инновации  Search Algorithms and Data Structures
Search Algorithms and Data Structures Холдинг «Строймаш-Вибропресс». Линия «Тенсиланд»
Холдинг «Строймаш-Вибропресс». Линия «Тенсиланд» Halloween and its origins
Halloween and its origins Язык программирования Turbo Pascal
Язык программирования Turbo Pascal Философия революционных демократов
Философия революционных демократов Подарки в деловых отношениях
Подарки в деловых отношениях Автоматическая коробка передач
Автоматическая коробка передач История управленческой мысли
История управленческой мысли Müssen
Müssen Консультация по общей и неорганической химии
Консультация по общей и неорганической химии  《汉语口语速成 基础篇》 第三课 在校园里 作者 支悠儿
《汉语口语速成 基础篇》 第三课 在校园里 作者 支悠儿