Содержание
- 2. Георг Кантор (03.03.1845 - 06.01.1918) немецкий математик.
- 3. Бертран Расселл 18 мая 1872 — 2 февраля 1970 — английский математик, философ и общественный деятель
- 4. Феликс Эдуард Жустин Эмиль Борель (7 января 1871 — 3 февраля 1956) — французский математик и
- 5. Понятие множества Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m
- 6. Введение в теорию множеств 1. Основные определения, терминология Под множеством А мы понимаем совокупность объектов произвольной
- 7. Определение 1 Множество А называется подмножеством В, если для любого х ( ) Обозначение: Другими словами,
- 8. Определение 3 Множества А и В называются равными, если они состоят из одних и тех же
- 9. Определение 5 тогда и только тогда, когда и . Теорема 6 Для любых множеств А, В,
- 10. 2. Операции над множествами Определение 1 Объединением двух множеств А и В называется множество Пример Пусть
- 11. Объединение множеств Теорема 2 Пусть А, В, С – произвольные множества. Тогда: а) – идемпотентность объединения;
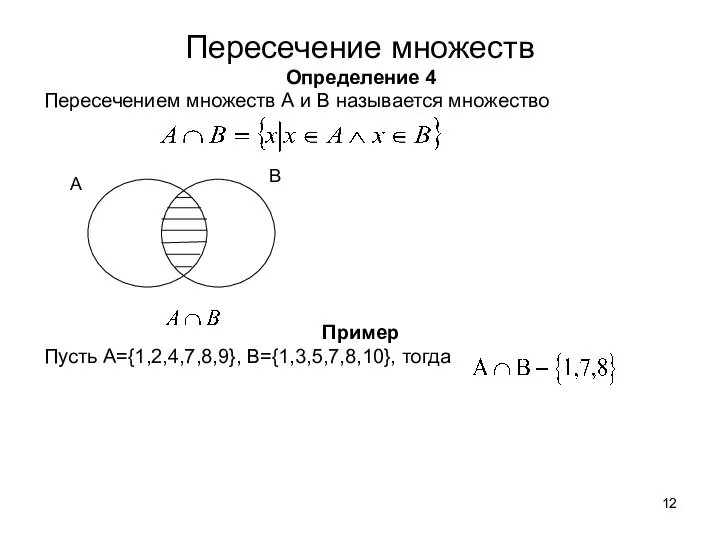
- 12. Пересечение множеств Определение 4 Пересечением множеств А и В называется множество Пример Пусть A={1,2,4,7,8,9}, B={1,3,5,7,8,10}, тогда
- 13. Теорема 5 Пусть А, В, С – произвольные множества, тогда: а) - идемпотентность пересечения; б) -
- 14. Объединение и пересечение множеств Теорема 6 1) 2) 3) 4)
- 15. Разность множеств, дополнение, симметрическая разность Определение 1 Разностью множеств A и B называется множество . Пример
- 16. Разность множеств Теорема 2 Пусть А, В, С – произвольные множества, тогда: 1) 2) 3) 4)
- 17. Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его подмножествами. Понятие
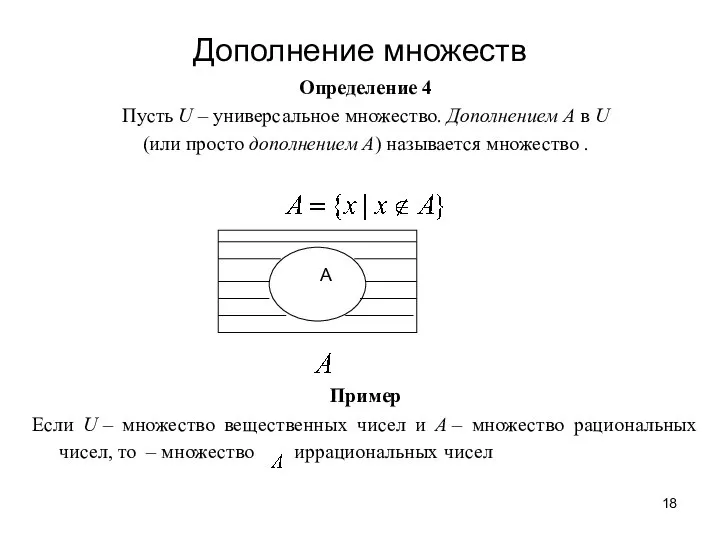
- 18. Дополнение множеств Определение 4 Пусть U – универсальное множество. Дополнением А в U (или просто дополнением
- 19. Дополнение множеств Теорема 5 1) 2) 3) Теорема 6(законы Моргана для дополнений) а) ; б) .
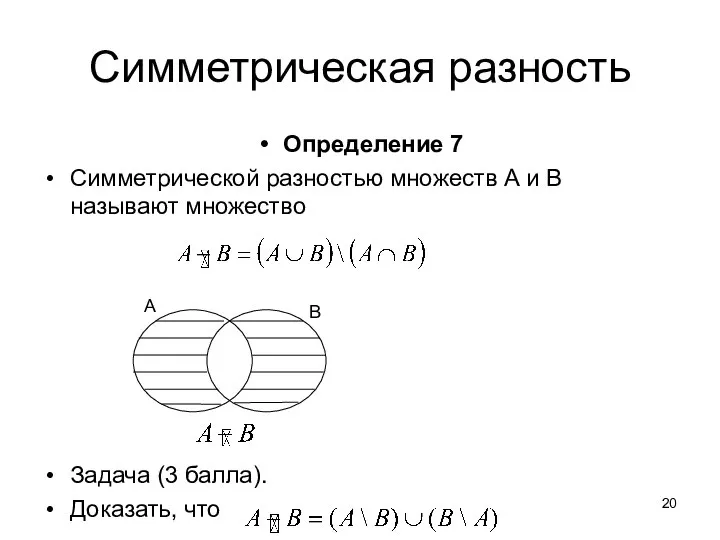
- 20. Симметрическая разность Определение 7 Симметрической разностью множеств A и B называют множество Задача (3 балла). Доказать,
- 21. Парадокс Расселла Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента.
- 22. Другие формулировки парадокса Расселла Парадокс Брадобрея: Одному деревенскому брадобрею приказали «брить всякого, кто сам не бреется,
- 23. Решение задач
- 24. 1. Вычисление множеств Дано U={1;2;3;4;5;6;7;8;9;10;11}, A={1;2;3;7;9}, B={3;4;5;6;10;11}, C={2;3;4;7;8}, D={1;7;11}. Вычислить множества 1) 2) 3) 4) 5)
- 25. 2. Выражение множеств Пусть U={1, 2, 3, 4, 5, 6, 7, 8,9}, A={1, 2, 3, 5},
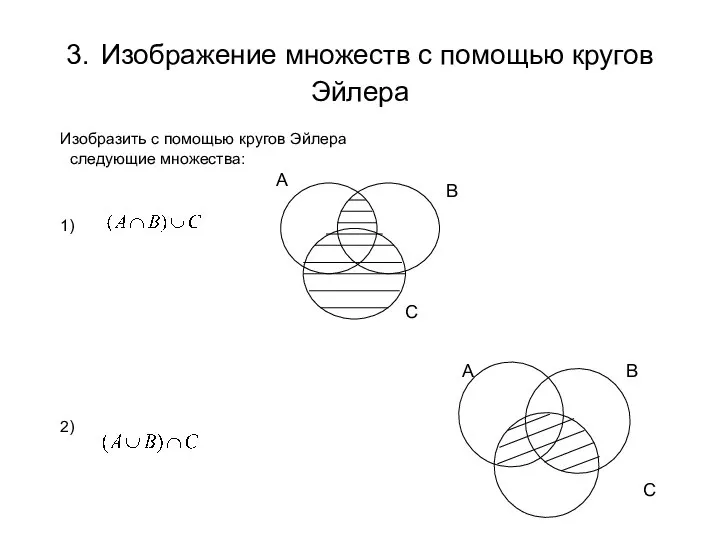
- 26. 3. Изображение множеств с помощью кругов Эйлера Изобразить с помощью кругов Эйлера следующие множества: 1) 2)
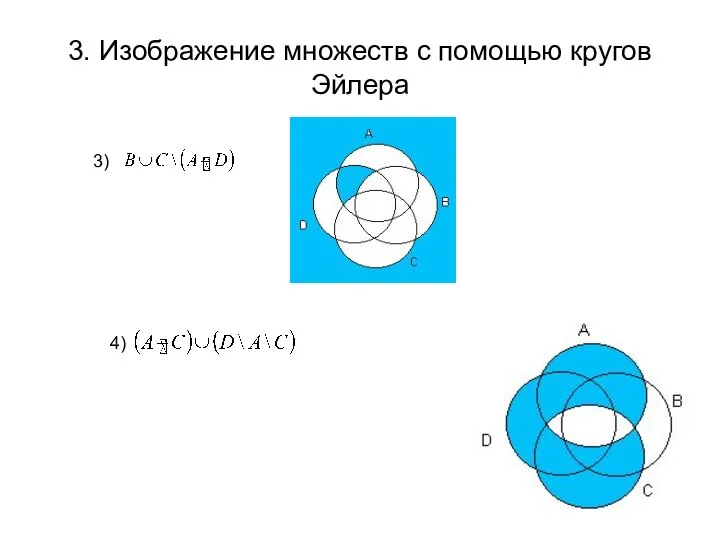
- 27. 3. Изображение множеств с помощью кругов Эйлера 3) 4)
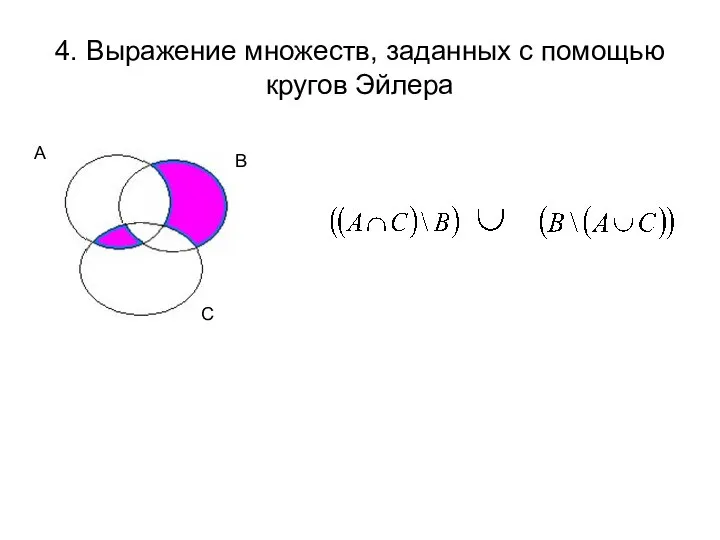
- 28. 4. Выражение множеств, заданных с помощью кругов Эйлера
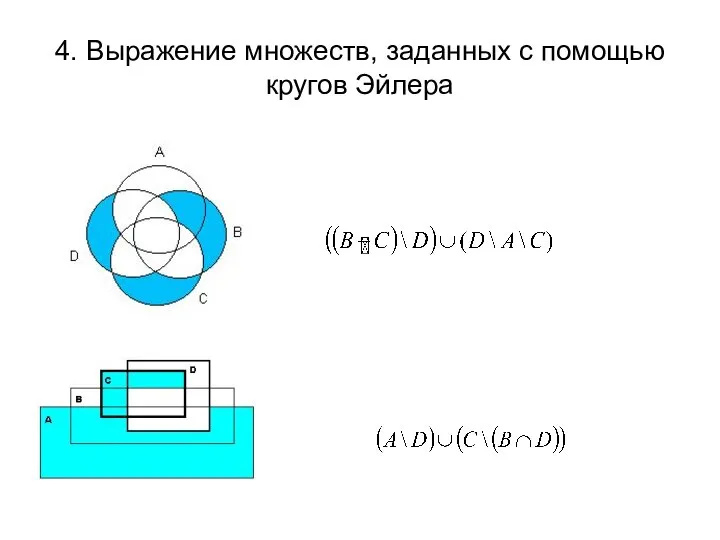
- 29. 4. Выражение множеств, заданных с помощью кругов Эйлера
- 30. Декартово произведение
- 31. Декартово произведение Под упорядоченной парой (а; b) мы будем понимать двухэлементное множество, состоящее из элементов а
- 32. Декартово произведение Определение 2 а) Множество называется декартовым произведением n множеств; б) - (n cомножителей) –
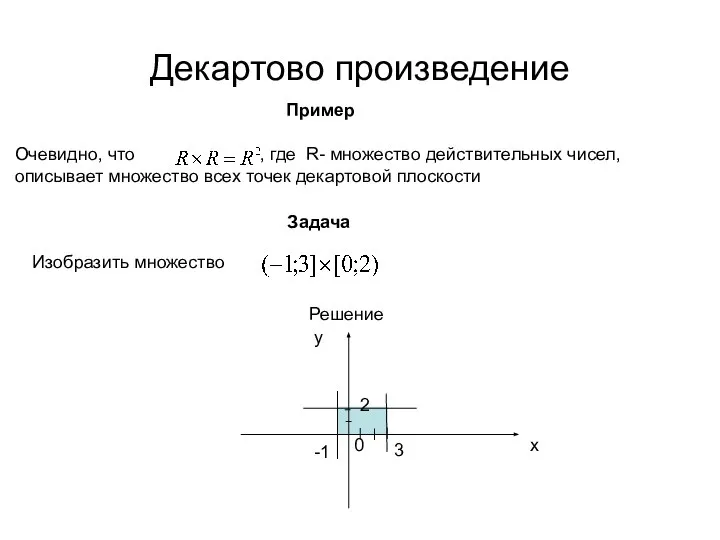
- 33. Декартово произведение Задача Изобразить множество Пример Очевидно, что , где R- множество действительных чисел, описывает множество
- 34. Декартово произведение Теорема 3 Пусть А, В, С – произвольные множества, тогда
- 36. Скачать презентацию

























 Презентация "Скульптуры разных эпох и стилей" - скачать презентации по МХК
Презентация "Скульптуры разных эпох и стилей" - скачать презентации по МХК Гимнастическая терминология
Гимнастическая терминология Как я провёл Лето
Как я провёл Лето Проект фильма "Шалаш"
Проект фильма "Шалаш" Мастер-класс. Решение задач по разделу «Механика»
Мастер-класс. Решение задач по разделу «Механика» Спорт - Дело Тонкое. СпецВыпуск
Спорт - Дело Тонкое. СпецВыпуск Врубель Михаил Александрович ЖИЗНЬ И ТВОРЧЕСТВО ВЕЛИКОГО РУССКОГО ХУДОЖНИКА.
Врубель Михаил Александрович ЖИЗНЬ И ТВОРЧЕСТВО ВЕЛИКОГО РУССКОГО ХУДОЖНИКА.  Бог никогда не спит
Бог никогда не спит Интерьер-студия Felicita. Уют Вашего дома!
Интерьер-студия Felicita. Уют Вашего дома! Политология как наука и учебная дисциплина
Политология как наука и учебная дисциплина Наскільки важлива культура зовнішнього вигляду вчителя
Наскільки важлива культура зовнішнього вигляду вчителя МЕТОД ПРОЕКТОВ В ОБРАЗОВАНИИ "Метод проектов - это не алгоритм, состоящий из четких этапов, а модель творческого мышления и п
МЕТОД ПРОЕКТОВ В ОБРАЗОВАНИИ "Метод проектов - это не алгоритм, состоящий из четких этапов, а модель творческого мышления и п Средний восток в международных отношениях после окончания холодной войны
Средний восток в международных отношениях после окончания холодной войны Олимпийские медали
Олимпийские медали хип-хоп
хип-хоп Строительство и усиление военных дорог
Строительство и усиление военных дорог Сервисный тренинг EXD06 3,0l-V6-TDI-CR-двигатель в Phaeton
Сервисный тренинг EXD06 3,0l-V6-TDI-CR-двигатель в Phaeton The 19th amendment: the equal rights
The 19th amendment: the equal rights Устрій та бойове застосування КЗА 86Ж6. Методика розрахунку змінних величин. Запис змінних величин. (Тема 11.3)
Устрій та бойове застосування КЗА 86Ж6. Методика розрахунку змінних величин. Запис змінних величин. (Тема 11.3) Soudage, qu'est-ce que ce
Soudage, qu'est-ce que ce ВКР: Основные характеристики технологии PON
ВКР: Основные характеристики технологии PON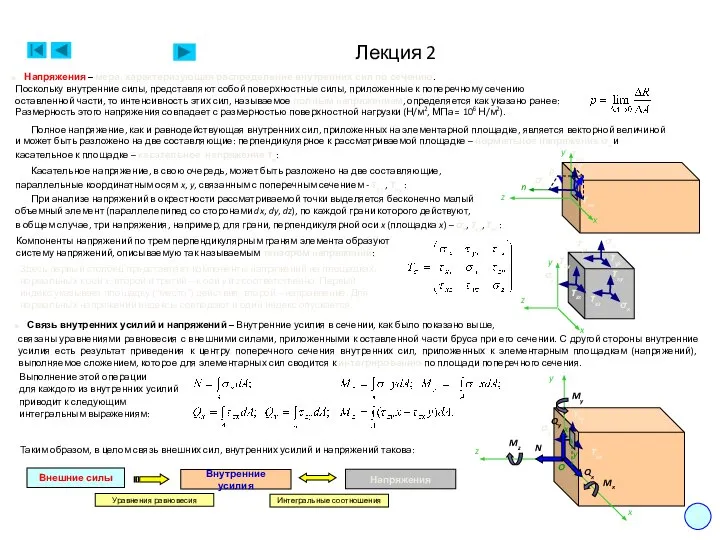 Напряжения. Связь внутренних усилий и напряжений
Напряжения. Связь внутренних усилий и напряжений Презентация "Филимоновская игрушка" - скачать презентации по МХК
Презентация "Филимоновская игрушка" - скачать презентации по МХК Русская народная игрушка
Русская народная игрушка Аттестационная работа. Метод проектов на занятиях инженерной графикой
Аттестационная работа. Метод проектов на занятиях инженерной графикой Технология разработки программного обеспечения
Технология разработки программного обеспечения Принципы радиосвязи. (8 класс)
Принципы радиосвязи. (8 класс) Реализм в русской литературе 19 века
Реализм в русской литературе 19 века