Задача о Кёнигсбергских мостах
Впервые над задачей описанного выше типа задумался Леонард
Эйлер после посещения города Кенигсберга (ныне Калининград).
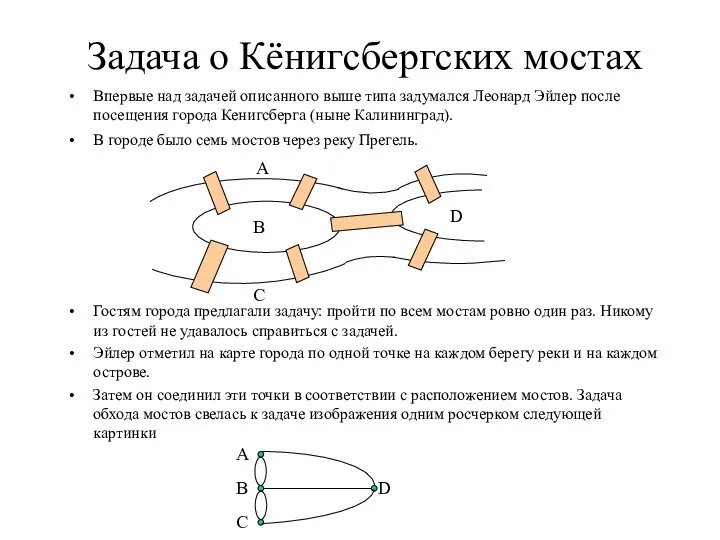
В городе было семь мостов через реку Прегель.
Гостям города предлагали задачу: пройти по всем мостам ровно один раз. Никому из гостей не удавалось справиться с задачей.
Эйлер отметил на карте города по одной точке на каждом берегу реки и на каждом острове.
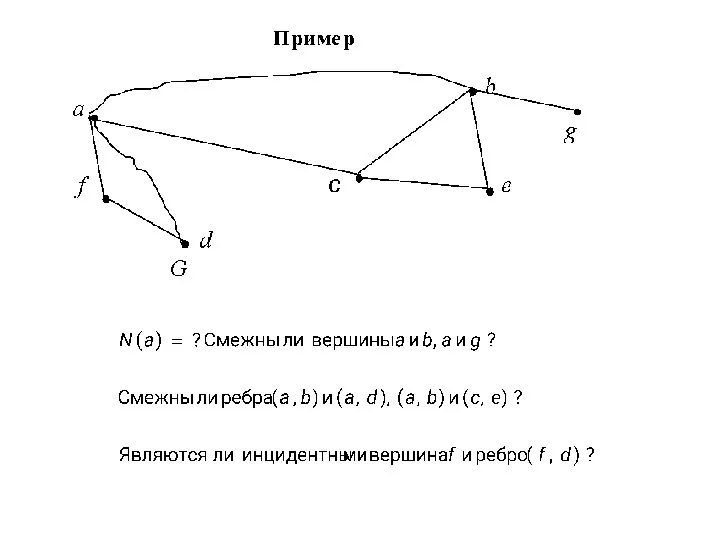
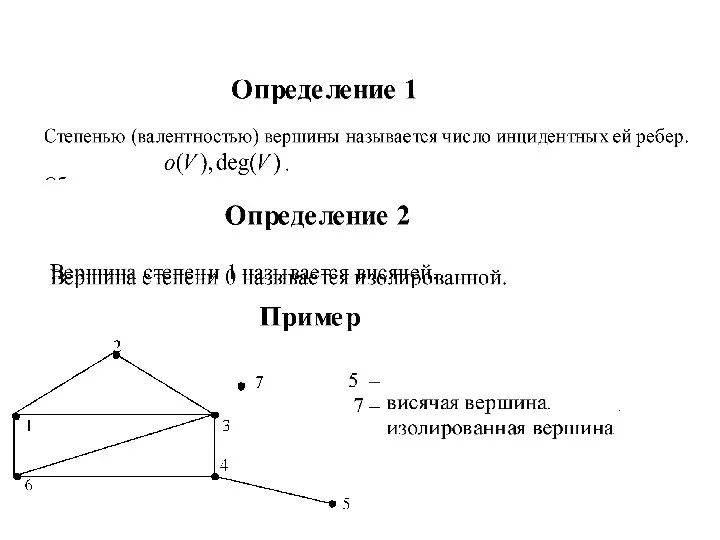
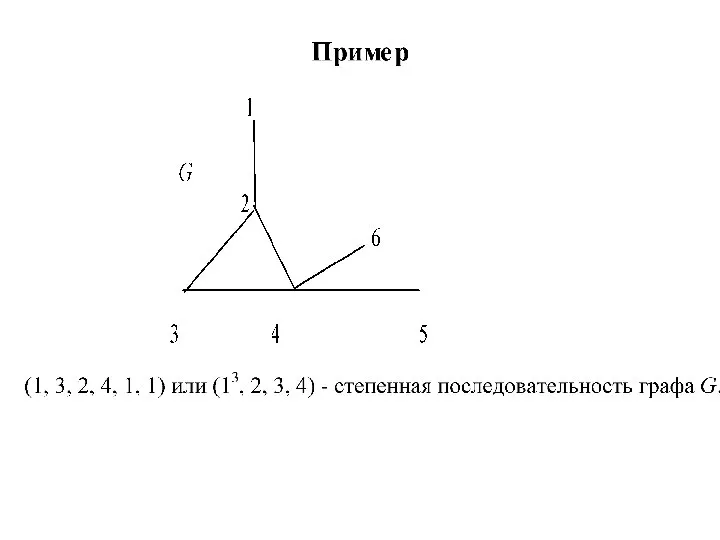
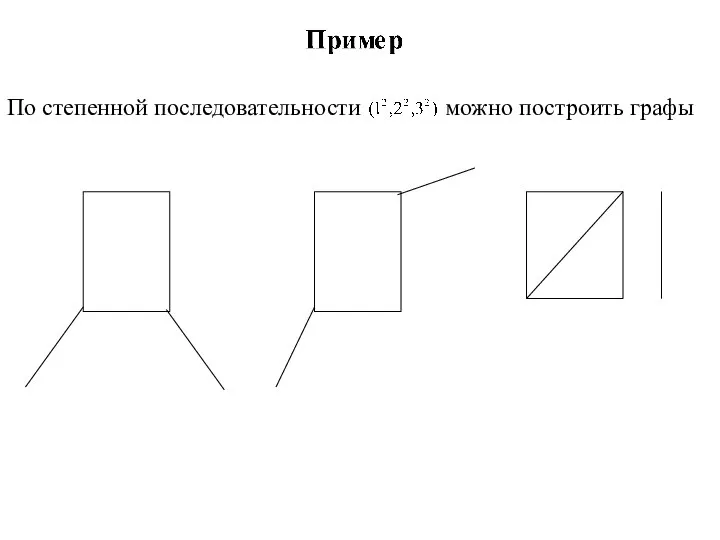
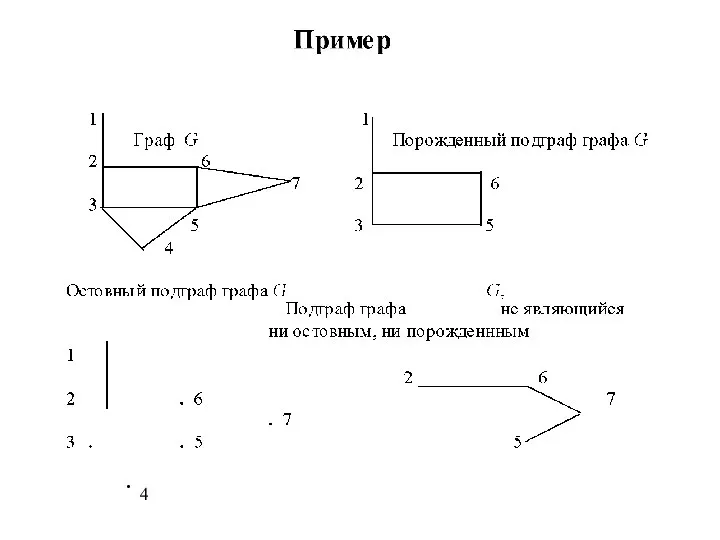
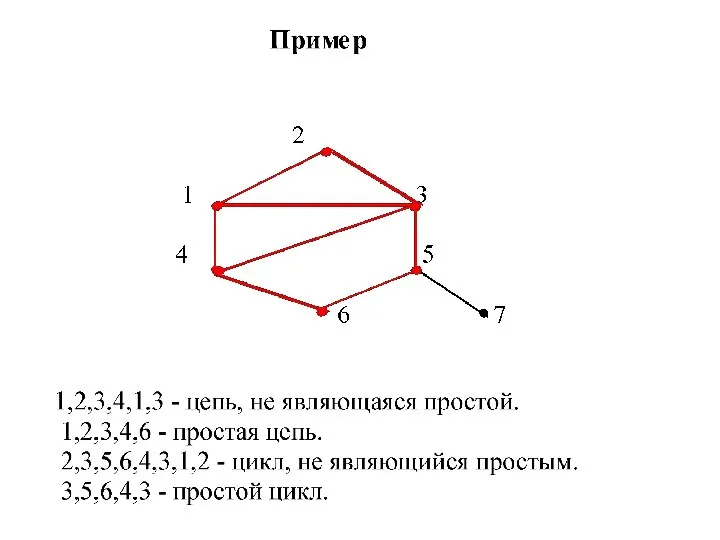
Затем он соединил эти точки в соответствии с расположением мостов. Задача обхода мостов свелась к задаче изображения одним росчерком следующей картинки
B
A
C
D




















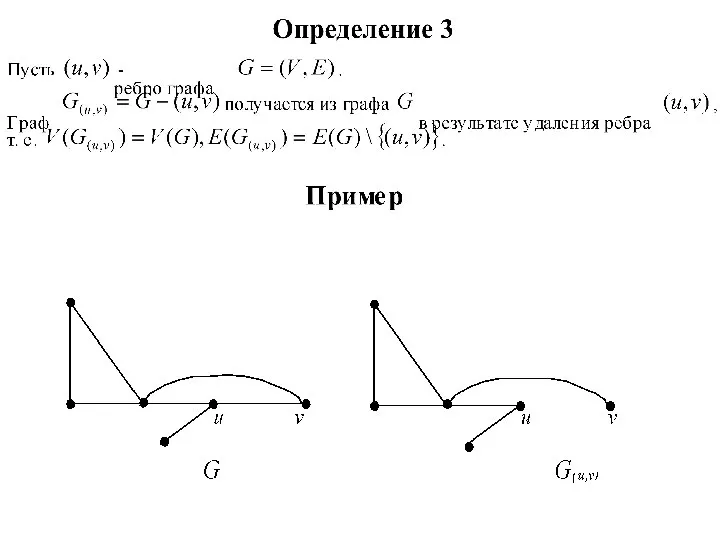
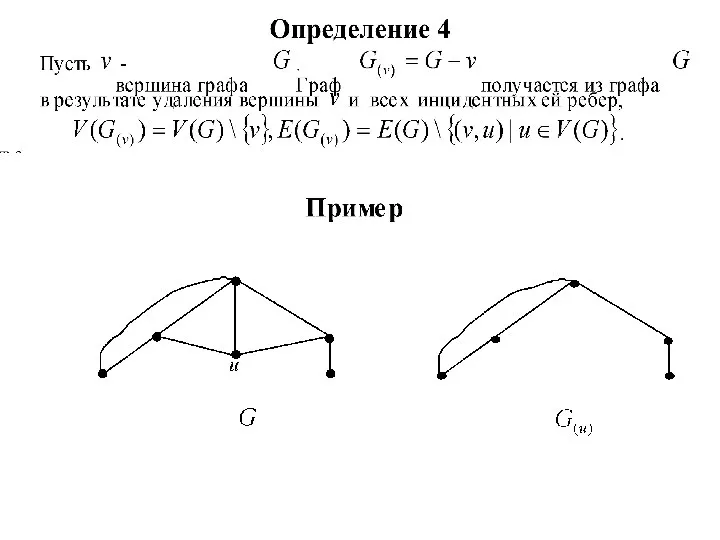
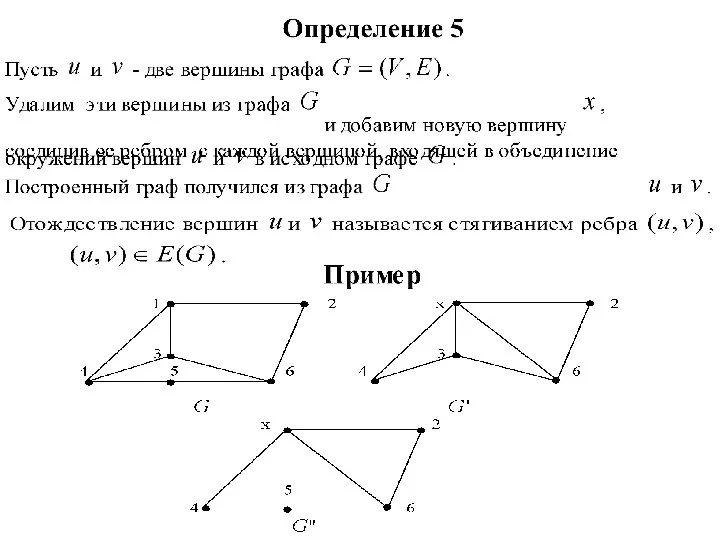
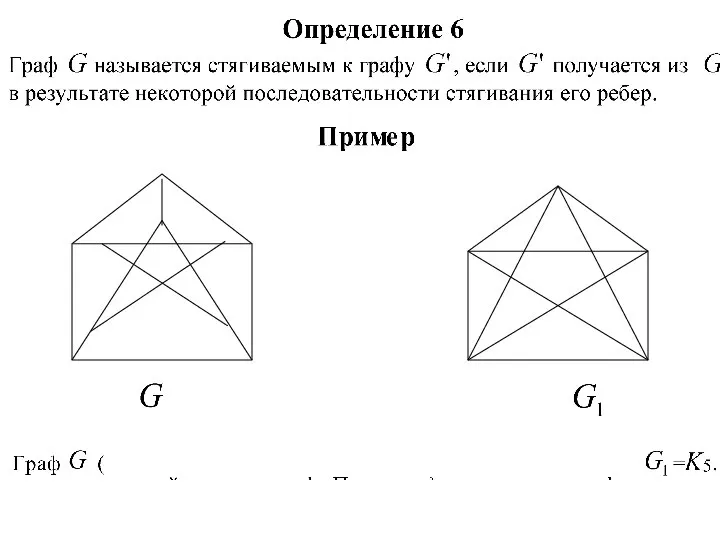





 Рационализм политических взглядов Н. Макиавелли
Рационализм политических взглядов Н. Макиавелли Взаимное положение двух прямых
Взаимное положение двух прямых  Программа Eurocode для расчета несущих конструкций строительных сооружений. (Лекция 3)
Программа Eurocode для расчета несущих конструкций строительных сооружений. (Лекция 3) Ферменты 2.ppt
Ферменты 2.ppt Презентация Основные виды логистической деятельности
Презентация Основные виды логистической деятельности Античная Философия
Античная Философия Конституция ФРГ 1949 года и Конституция РФ 1993 года
Конституция ФРГ 1949 года и Конституция РФ 1993 года Введение в объекты Java
Введение в объекты Java Теория врожденных знаний Выполнили : Елена Данильченко и Ольга Ярош 2 курс, лого-1
Теория врожденных знаний Выполнили : Елена Данильченко и Ольга Ярош 2 курс, лого-1  Теория принятия решений
Теория принятия решений Проблема развития массового спорта на страницах районных СМИ
Проблема развития массового спорта на страницах районных СМИ Ограниченные вещные права
Ограниченные вещные права Многокоординатное устройство цифрового управления
Многокоординатное устройство цифрового управления Выполнил: ученик 1 класса б МОУ «Лицей №15» им. акад. Ю.Б. Харитона Мараханов Владислав Александрови
Выполнил: ученик 1 класса б МОУ «Лицей №15» им. акад. Ю.Б. Харитона Мараханов Владислав Александрови Стенокардия
Стенокардия  Генеалогічна класифікація мов. Лінгвокомпаративістика
Генеалогічна класифікація мов. Лінгвокомпаративістика Хэллоуин
Хэллоуин Пермь, фото памятных мест
Пермь, фото памятных мест Презентация Microsoft PowerPoint (2)
Презентация Microsoft PowerPoint (2) Тренируем руку. Правила написания иероглифов
Тренируем руку. Правила написания иероглифов Цифровые многоканальные телекоммуникационные системы
Цифровые многоканальные телекоммуникационные системы Nike теория управление
Nike теория управление Тригонометрическая интерполяция
Тригонометрическая интерполяция  Выполнение нашего домашнего задания из СГТУ имени Гагарина «МКОУ СОШ№5 г. Ершова
Выполнение нашего домашнего задания из СГТУ имени Гагарина «МКОУ СОШ№5 г. Ершова Технология работы на складе
Технология работы на складе Презентация на тему "ЖЕСТОКОЕ ОБРАЩЕНИЕ С ДЕТЬМИ" - скачать презентации по Педагогике
Презентация на тему "ЖЕСТОКОЕ ОБРАЩЕНИЕ С ДЕТЬМИ" - скачать презентации по Педагогике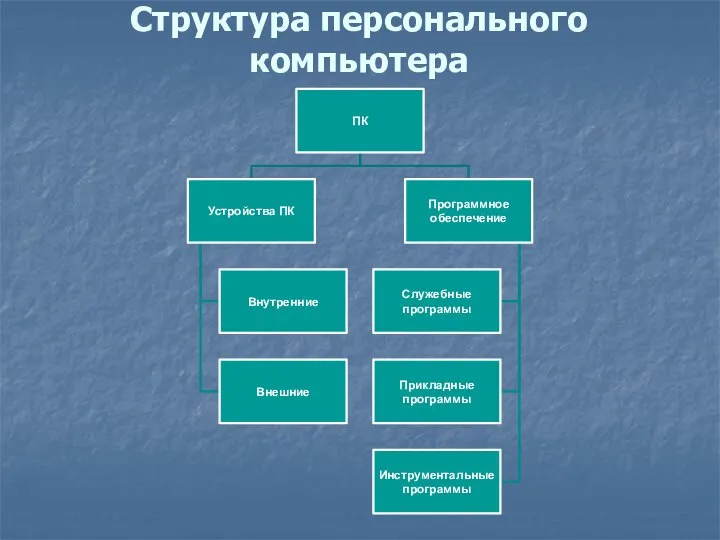 Структура персонального компьютера
Структура персонального компьютера Исламский фундаментализм
Исламский фундаментализм