Содержание
- 2. ЛЕКЦИЯ № 1 по дисциплине «Физика, математика» на тему: «Основы теории вероятностей» для курсантов и студентов
- 3. Кафедра биологической и медицинской физики — одна из первых кафедр Военно-медицинской академии и старейшая кафедра физики
- 4. Здание Естественно-исторического института
- 5. Первым профессором кафедры стал Василий Владимирович Петров (1761—1834) — знаменитый русский ученый-естествоиспытатель, заложивший основы преподавания экспериментальной
- 6. Понятие "Evidence-based Medicine", или "медицины, основанной на доказательствах" (доказательной медицины) было предложено канадскими учеными из университета
- 7. Доказательная медицина подразумевает добросовестное, точное и осмысленное использование лучших результатов клинических исследований для выбора лечения конкретного
- 8. Увеличение объема научной информации, в частности в области клинической фармакологии. Нехватка средств, связанных с расходами на
- 9. Авторитет врача ("увеличение числа однотипных ошибок с увеличением стажа работы") Страстность ("эмоциональное воздействие на более спокойных
- 10. По современным стандартам надежная оценка эффективности методов лечения и профилактики может быть получена только в ходе
- 11. По окончании исследования сопоставляются частоты наступления клинически важных исходов – выздоровления, осложнения, смерти, а не суррогатные
- 12. Для получения выводов исследования необходимо учитывать неопределенность многих характеристик, а также конечность числа наблюдений. Наиболее приемлемым
- 13. «Статистика – это совокупность методов, которые дают нам возможность принимать оптимальные решения в условиях неопределенности» (А.
- 14. 1. Случайные события. Предмет теории вероятности. Определение вероятности (статистическое и классическое).
- 15. Случайные события – это явления и факты, которые при различных условиях могут происходить или не происходить.
- 16. Изучение закономерностей однородных массовых (статистических)случайных событий составляет предмет теории вероятности и основанной на ней математической статистики.
- 17. Изучение каждого отдельного явления с выполнением определенного комплекса условий называется испытанием (опытом, экспериментом). Всякий результат или
- 18. Возможность появления каждого события определяется специальной величиной – вероятностью наступления события – Р(А). Вероятность Р(А) –
- 19. В «классическом» определении вероятности вероятность случайного события определяется как отношение числа равновозможных исходов опыта, благоприятствующих наступлению
- 20. Из классического определения вероятности вытекает ряд ее свойств: Вероятность достоверного события, то есть события, которое происходит
- 21. Классическое определение вероятности случайного события применимо только к испытаниям с конечным числом исходов, причем исходов равновероятных.
- 22. Вероятностью случайного события называется предел, к которому стремится относительная частота события (частость)при неограниченном увеличении числа испытаний.
- 23. В отличие от классического подхода к определению вероятности случайного события, в соответствии с которым для нахождения
- 24. Статистическую вероятность события нельзя точно определить на основании конечного числа испытаний, каким бы большим оно ни
- 25. Пусть проведено 5 серий по 100 выстрелов в цель, осуществленных одним и тем же спортсменом в
- 26. Относительная частота попаданий в цель не является величиной постоянной, а изменяется от серии к серии. Эта
- 27. 2. Классификация событий. Понятие о совместных и несовместных, зависимых и независимых событиях. Теоремы сложения и умножения
- 28. а) Достоверными, невозможными и случайными; б) Противоположное событие – происходит только тогда, когда событие А не
- 29. в) Эквивалентные события – события с одинаковой вероятностью, независимо от их природы: Р(А) = Р(В); г)
- 30. д) Независимые события – вероятность события А не зависит от того, произошло ли событие В. В
- 31. В ряде случаев вычислить вероятность события оказывается проще, если представить его в виде комбинации более простых
- 32. Вероятность появления одного (безразлично какого) события из нескольких несовместных событий равна сумме вероятностей этих событий. Р
- 33. Например, вероятность выпадения четного числа на верхней грани игральной кости: Р (2 или 4 или 6)
- 34. Вероятность одновременного появления двух или более независимых событий равна произведению их вероятностей. Р (А и В
- 35. Пример: Найти вероятность того, что в семье из трех детей родятся два сына и одна дочь.
- 36. Если вероятность события А меняется в связи с появлением или непоявлением события В, то событие А
- 37. Вероятность появления двух зависимых событий одновременно равна произведению вероятности одного из них на условную вероятность второго
- 38. Пример: студент пришел на экзамен, зная 40 вопросов из 50. Найти вероятность того, что он ответит
- 39. Искомая вероятность: Р (АхВхС) = Р (А) х Р (В/А) х Р (С/АхВ) = = 40/50
- 40. 3. Непрерывные и дискретные случайные величины. Распределения дискретных случайных величин, их характеристики: математическое ожидание, дисперсия, среднее
- 41. Науку об измерениях физических величин и способах обеспечения необходимой точности этих измерений называют метрологией. Под физической
- 42. Основой для количественной оценки физической величины является единица измерения физической величины. Единицы измерения физических величин группируются
- 43. В Международной системе единиц (СИ) основными единицами являются метр (м), килограмм массы (кг), секунда (с), моль
- 44. Величины, которые в зависимости от стечения случайных обстоятельств могут принимать различные значения, причем заранее неизвестно, какое
- 45. Случайная величина называется дискретной, если совокупность всех ее возможных значений представляет собой конечное или бесконечное, но
- 46. Вероятность того, что дискретная случайная величина Х в i-м опыте примет значение xi, равна pi =
- 47. Закон или функция распределения могут быть заданы графически, аналитически или в форме таблицы. Пример: Имеется 10
- 48. Возможными значениями рассматриваемой случайной величины являются (в порядке возрастания) 8, 9, 10, 11 и 12. Вероятность
- 49. Искомый закон распределения имеет вид:
- 50. На практике закон распределения дискретной случайной величины часто неизвестен, но для определения особенностей случайной величины используют
- 51. Математическим ожиданием случайной величины называется сумма произведений всех возможных значений этой величины на вероятности этих значений.
- 52. Например, если использовать данные предыдущего примера, то математическое ожидание M (X) = 8 . 0,2 +
- 53. Отдельные значения случайной величины группируются около математического ожидания. Степень рассеивания (разброса) характеризуется дисперсией. Дисперсией называется математическое
- 54. На практике дисперсию часто удобнее вычислять по формуле: D (X) = σ2 = M (X 2)
- 55. Средним квадратическим отклонением (стандартным отклонением) случайной величины называют корень квадратный из дисперсии. Для нашего примера σ
- 56. Случайная величина, принимающая любые значения в определенном интервале, называется непрерывной. Примеры: мгновенные значения скорости теплового движения
- 57. Так как невозможно перечислить все значения непрерывной случайной величины и указать их вероятности, то промежуток между
- 58. Плотность вероятности, или функция распределения вероятностей [f (x)], показывает, как изменяется вероятность dP, отнесенная к интервалу
- 59. Вероятность того, что случайная величина принимает какое-либо значение в интервале (a,b):
- 60. Условие нормирования непрерывной случайной величины:
- 61. Математическое ожидание и дисперсия непрерывной случайной величины рассчитываются по формулам:
- 62. Нормальный закон распределения (закон Гаусса): Примеры распределений непрерывных случайных величин: Нормальный закон распределения
- 63. Здесь: a = M(x) – математическое ожидание случайной величины, σ – среднее квадратическое отклонение (соответственно, σ2
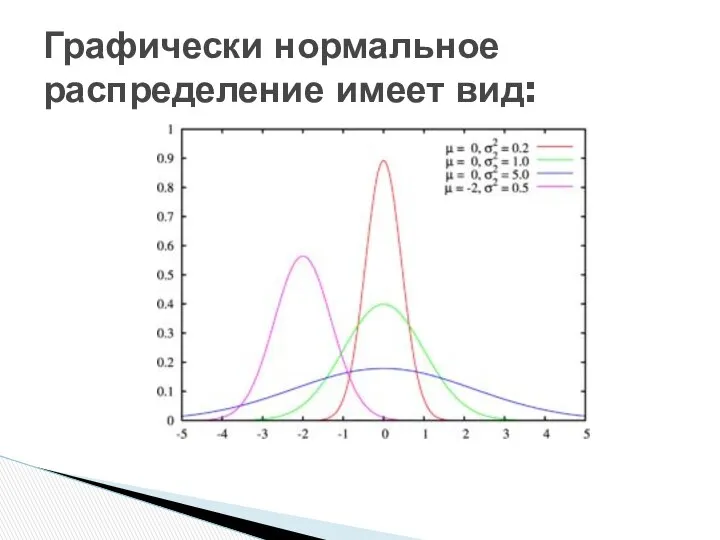
- 64. Графически нормальное распределение имеет вид:
- 65. Кривая имеет колоколообразную форму, симметричную относительно точки х = a. Величина f (X ) в этой
- 66. При изменении параметра a форма нормальной кривой не изменяется, график сдвигается влево или вправо. При изменении
- 67. Важное значение нормального распределения во многих областях науки, например, в математической статистике и статистической физике, вытекает
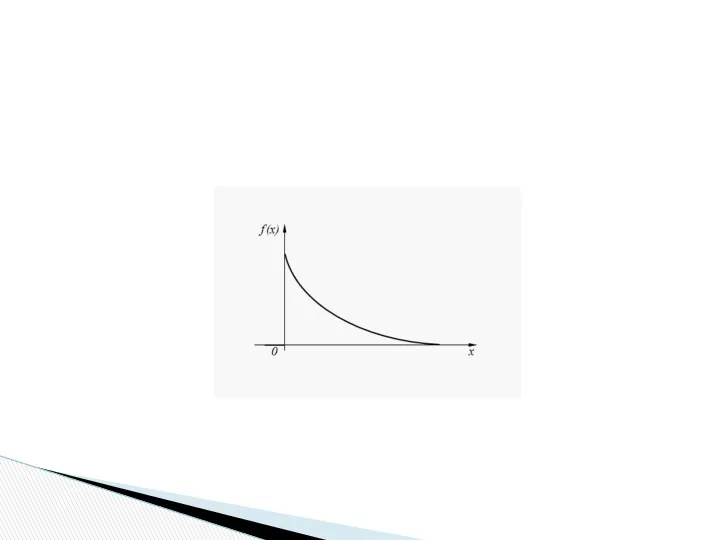
- 68. Непрерывная случайная величина X, функция плотности вероятности которой задается выражением называется случайной величиной, имеющей показательное, или
- 71. Скачать презентацию
























































![Плотность вероятности, или функция распределения вероятностей [f (x)], показывает, как изменяется](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1307530/slide-57.jpg)









 РОДНОЙ ЯЗЫК ПРАКТИКА ПРЕПОДАВАНИЯ 16.09.19
РОДНОЙ ЯЗЫК ПРАКТИКА ПРЕПОДАВАНИЯ 16.09.19 Гимнастические упражнения как основной способ профилактики заболеваний у детей школьного возраста (11-13 лет)
Гимнастические упражнения как основной способ профилактики заболеваний у детей школьного возраста (11-13 лет) Зачем учить китайский
Зачем учить китайский Профессиональное обучение обучающихся на базе ГПОУ «МЖТ
Профессиональное обучение обучающихся на базе ГПОУ «МЖТ С. Хантингтон «Столкновение цивилизаций». Бжезинский «Великая шахматная доска». А. Богатуров «Великие державы на Тихом океане»
С. Хантингтон «Столкновение цивилизаций». Бжезинский «Великая шахматная доска». А. Богатуров «Великие державы на Тихом океане» ветр оспа история
ветр оспа история Креативные разработки: Слоган как инструмент брендинга
Креативные разработки: Слоган как инструмент брендинга Возрождение традиционного вепсского ремесла - ткачества
Возрождение традиционного вепсского ремесла - ткачества Слайдовая презентация «Зелёная аптека» Выполнила ученица 3 класса МОУ «Безрукавская СОШ» Слонова Анастасия_
Слайдовая презентация «Зелёная аптека» Выполнила ученица 3 класса МОУ «Безрукавская СОШ» Слонова Анастасия_ Теоретические и практические вопросы назначения наказания по совокупности преступлений
Теоретические и практические вопросы назначения наказания по совокупности преступлений Чертежи предметов с использованием геометрических построений
Чертежи предметов с использованием геометрических построений Порты ввода\вывода микроконтроллеров серии AVR. Внешние прерывания
Порты ввода\вывода микроконтроллеров серии AVR. Внешние прерывания Правила проведения соревнований «Формула будущего». Юношеские классы спортивных мотолодок
Правила проведения соревнований «Формула будущего». Юношеские классы спортивных мотолодок Алгоритм выполнения задания А27 (Информационная обработка письменных текстов различных стилей и жанров)
Алгоритм выполнения задания А27 (Информационная обработка письменных текстов различных стилей и жанров) Таблица умножения и деления на 4 Технологический приём анимированная сорбонка
Таблица умножения и деления на 4 Технологический приём анимированная сорбонка Президент Российской Федерации
Президент Российской Федерации Презентация "Презентация проекта" - скачать презентации по Экономике
Презентация "Презентация проекта" - скачать презентации по Экономике ВИЧ – инфекция и нейросифилис
ВИЧ – инфекция и нейросифилис Инвалидность. Получение инвалидности
Инвалидность. Получение инвалидности Русская культура 16-17 веков
Русская культура 16-17 веков Визуальная диагностика рахита Выполнила 307 ОМ Қойшыманова. А Проверила Қожахметова .Ж.Ж
Визуальная диагностика рахита Выполнила 307 ОМ Қойшыманова. А Проверила Қожахметова .Ж.Ж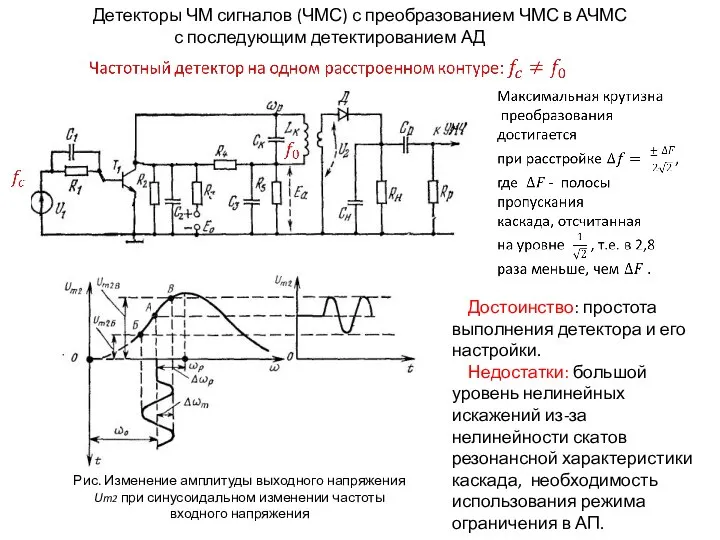 Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД
Детекторы ЧМ сигналов (ЧМС) с преобразованием ЧМС в АЧМС с последующим детектированием АД Российское искусство XIX века
Российское искусство XIX века Компания «ИТ-Кострома» мы расширяем ваши возможности. Предложение партнерам фирмы 1С
Компания «ИТ-Кострома» мы расширяем ваши возможности. Предложение партнерам фирмы 1С Московский Кремль
Московский Кремль Планета Земля
Планета Земля Свобода слова: философские основания, политологическое содержание и правовые основы
Свобода слова: философские основания, политологическое содержание и правовые основы Презентация "С нами надежнее!" - скачать презентации по Экономике
Презентация "С нами надежнее!" - скачать презентации по Экономике