Содержание
- 2. Законы теории вероятностей – это математическое выражение реальных закономерностей, которым подчиняются массовые случайные явления. При этом
- 3. Разработка методов получения, описания и анализа экспериментальных данных, определенных в результате исследования массовых случайных явлений, составляет
- 4. Статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми
- 5. Выборочное исследование всегда предпочтительнее: а) по экономическим причинам (меньшая трудоемкость), б) часто сплошное обследование нереально (необходимо
- 6. Статистическая совокупность, состоящая из всех объектов, которые (по крайней мере теоретически) подлежат исследованию, называется генеральной совокупностью,
- 7. Главная цель выборочного метода – по вычисленным числовым характеристикам выборки как можно точнее определить соответствующие характеристики
- 8. Изучаемое свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности, то есть выборка должна быть представительной
- 9. На практике всегда необходимо искать компромисс, чтобы исследуемые выборки были, с одной стороны, не слишком велики,
- 10. а) Статистический дискретный ряд распределения Пусть необходимо изучить распределение значений признака Х у объектов некоторой генеральной
- 11. Пусть в полученной выборке наименьшее значение x1 признака встречается m1 раз, следующее по величине значение x1
- 12. Если результаты наблюдений представить в виде таблицы, то получим: Здесь p – относительная частота.
- 13. Такую таблицу называют статистическим дискретным рядом распределения. Cтатистический дискретный ряд распределения – это совокупность вариант и
- 14. Для графического изображения подобного ряда на координатной плоскости откладывают точки (xi; mi) и соединяют их отрезками
- 15. Пример. Анализируемый показатель Х – срок лечения больного при некотором заболевании. Вариационный ряд – распределение больных
- 17. Очевидно, что представление результатов наблюдений в виде статистического дискретного ряда распределения на практике удобно лишь в
- 18. Для построения такого ряда всю область наблюдаемых значений изучаемого признака Х разбивают на некоторое небольшое количество
- 19. Пусть, например все наблюдавшиеся значения признака Х принадлежат интервалу (a,b). Разделим этот интервал на k равных
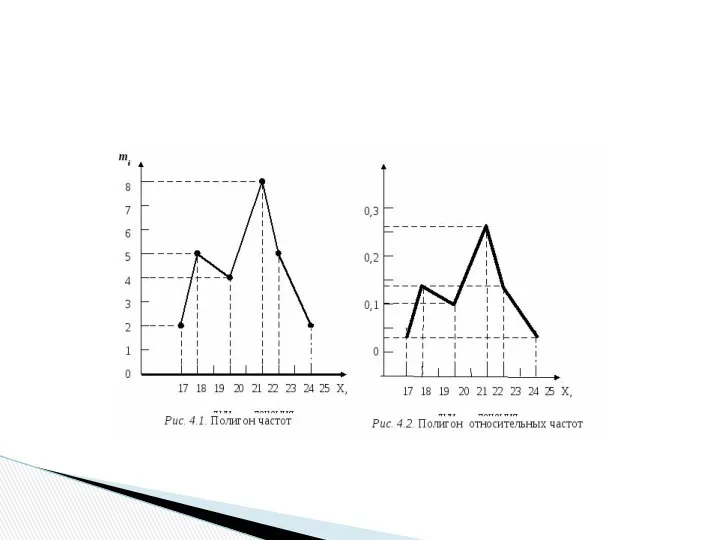
- 21. Графическим изображением статистического интервального ряда распределения является фигура, называемая полигоном частот (или относительных частот). Это совокупность
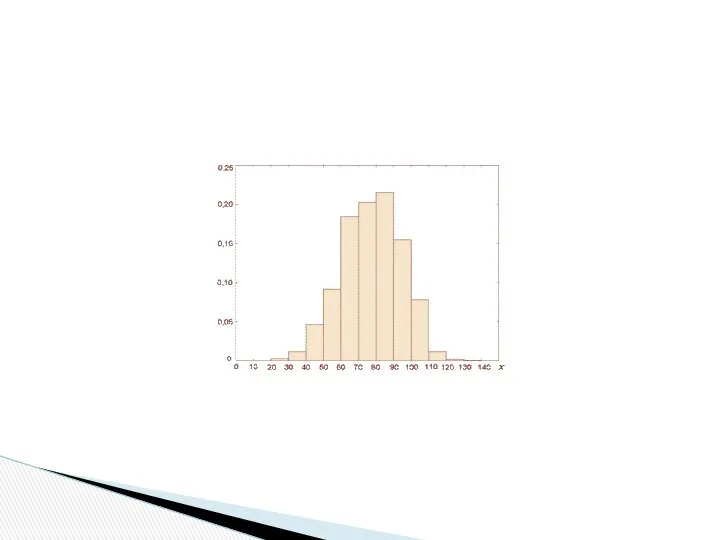
- 23. Площадь каждого прямоугольника равна: или Площадь гистограммы частот равна n, а площадь гистограммы относительных частот равна
- 24. Мода (Mo) равна варианте, которой соответствует наибольшая частота. Медиана (Ме) равна варианте, которая расположена в середине
- 25. Выборочная средняя – это среднее арифметическое вариант статистического ряда. где mi – частота встречаемости значения xi
- 26. Для характеристики рассеяния вариант вокруг среднего значения вводят характеристику, называемую выборочной дисперсией – среднее арифметическое квадратов
- 27. Корень квадратный из выборочной дисперсии называют выборочным средним квадратическим отклонением.
- 28. Предположим, что генеральная совокупность является нормальным распределением. Нормальное распределение полностью определено математическим ожиданием и средним квадратическим
- 29. Как и для выборки, для генеральной совокупности можно определить генеральную среднюю - среднее арифметическое значение всех
- 30. Рассеяние значений изучаемого признака генеральной совокупности оценивают генеральной дисперсией или генеральным средним квадратическим отклонением.
- 31. а) Точечные оценки Оценка характеристики распределения называется точечной, если она определяется одним числом, которому приближенно равна
- 32. Наилучшей оценкой генеральной средней является средняя выборочная:
- 33. Наилучшей точечной оценкой генеральной дисперсии является так называемая исправленная выборочная дисперсия , определяемая по формуле:
- 34. Наилучшей точечной оценкой генерального среднего квадратического отклонения является исправленное выборочное среднее квадратическое отклонение.
- 35. Точечные оценки параметров генеральной совокупности справедливы лишь при достаточно большом объеме выборки. При небольшом объеме выборки
- 36. Иначе говоря, р определяет вероятность того, что осуществляются следующие неравенства: где положительное число ε характеризует точность
- 37. Чем шире доверительный интервал, тем выше доверительная вероятность, и наоборот. При решении статистических задач в фармации,
- 38. Кроме доверительной вероятности, используют противоположное понятие – уровень значимости (вероятность непопадания генеральной средней в доверительный интервал).
- 39. При оценке генеральной средней по результатам выборочных наблюдений в предположении нормального распределения признака в генеральной совокупности
- 40. Определяют полуширину доверительного интервала для интервальной оценки генеральной средней при заданной доверительной вероятности р по формуле:
- 41. Интервальная оценка генеральной средней может быть использована для оценки истинного значения измеряемой величины. Пусть несколько раз
- 43. Скачать презентацию






































 Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС
Развитие самостоятельной и творческой активности учащихся на уроках математики в условиях введения ФГОС Презентация на тему "Правила поведения для воспитанных детей" - скачать презентации по Педагогике
Презентация на тему "Правила поведения для воспитанных детей" - скачать презентации по Педагогике Муниципальное образовательное учреждение Средняя общеобразовательная школы № 76
Муниципальное образовательное учреждение Средняя общеобразовательная школы № 76 Симптоматология заболеваний желчевыделительной системы
Симптоматология заболеваний желчевыделительной системы Вечные и земные ценности
Вечные и земные ценности Культура стран халифата
Культура стран халифата Глаголы с изменяющейся корневой гласной
Глаголы с изменяющейся корневой гласной Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены
Все подвиги Геракл совершил на службе А) у Зевса Б) у Эврисфея В) у Алкмены ЧЕМ БОЛЕЛ ВЕЛИКИЙ ВАН ГОГ? La tristesse durera toujours («Печаль будет длиться вечно»)
ЧЕМ БОЛЕЛ ВЕЛИКИЙ ВАН ГОГ? La tristesse durera toujours («Печаль будет длиться вечно»)  Радиационный контроль объектов и территорий
Радиационный контроль объектов и территорий Презентация Государственный флаг РФ
Презентация Государственный флаг РФ Опыт использования бизнес-моделей в процессе обучения предпринимательству в магистратуре Екатерина Бузулукова к.э.н., ст.преп
Опыт использования бизнес-моделей в процессе обучения предпринимательству в магистратуре Екатерина Бузулукова к.э.н., ст.преп Теоретические основы развития зависимого поведения у детей и подростков
Теоретические основы развития зависимого поведения у детей и подростков  Метрические свойства проекций. (Лекция 3)
Метрические свойства проекций. (Лекция 3) нейропсихология
нейропсихология Non scholae, sed vitae discimus
Non scholae, sed vitae discimus Tea tradition in Britain
Tea tradition in Britain Вещества и растворы для обеззараживания
Вещества и растворы для обеззараживания Семейная компания Bandi. Профессиональная косметика
Семейная компания Bandi. Профессиональная косметика Тема урока: Здоровый человек – здоровый сон. О правильном питании.
Тема урока: Здоровый человек – здоровый сон. О правильном питании. Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария
Федор Александрович Васильев Подготовила ученица 10 класса Бутикова Мария Управленческие решения в организациях
Управленческие решения в организациях Древнегреческая вазопись, как яркий пример античного искусства
Древнегреческая вазопись, как яркий пример античного искусства ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор,
ФИНАНСОВЫЙ КРИЗИС: причины возникновения и пути выхода Берзон Н.И. Д.э.н., профессор, Карданные передачи
Карданные передачи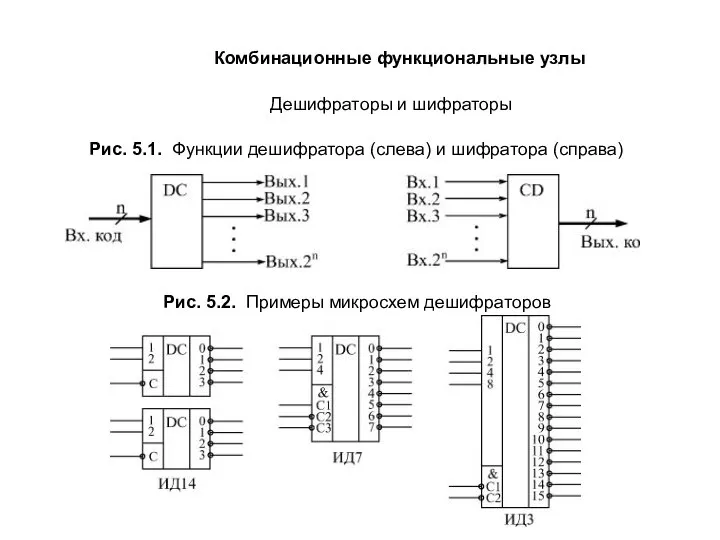 Комбинационные узлы
Комбинационные узлы Китай
Китай Этика приветствий и представлений
Этика приветствий и представлений