Содержание
- 2. План 1 Общие положения 2 Понятие о типовых режимах САУ 3 Теорема о предельном значении оригинала
- 3. 1 Общие положения Точность является важнейшим критерием качества систем. В настоящее время практически все многочисленные элементы
- 4. 2 Понятие о типовых режимах САУ Точность САУ принято оценивать по величине ошибок в типовых режимах.
- 5. ε Итак, нам необходимо вычислить установившуюся ошибку ε(t) при t→∞, при типовых режимах и по ней
- 6. 3 Теорема о предельном значении оригинала и методика определения установившихся ошибок Сформулируем для этого теорему о
- 7. Передаточная функция САУ по ошибке: Итак, чтобы определить установившуюся (при t→ ∞) ошибку САУ нужно: -
- 8. 4 Ошибки статических и астатических САУ в типовых режимах Рассмотрим ошибки САУ в типовых режимах: 1.
- 9. По теореме о предельном значении аргумента (1) Подставляя Wp(s) в (1) получим:
- 10. Статическая ошибка в статической САУ в (1+К) раз меньше входной величины.
- 11. Пусть теперь - астатическая САУ (есть интегратор, т.е. множитель S в знаменателе передаточной функции)
- 12. Таким образом, статическая ошибка в астатической САУ равна 0 Таким образом, статическая ошибка в астатической САУ
- 13. 2. Второй типовой режим - движение с постоянной скоростью (скоростная ошибка) x(t)=at a=cost Пусть: - статическая
- 14. Ошибка в статической САУ при линейно-нарастающем входном сигнале x(t)=at возрастает до ∞. Т.о. статические САУ в
- 15. Пусть теперь - астатическая САУ Тогда
- 16. Т.о. в астатических САУ при x(t)=at a=const устанавливается ошибка в “К” раз меньше чем “a”, т.е.
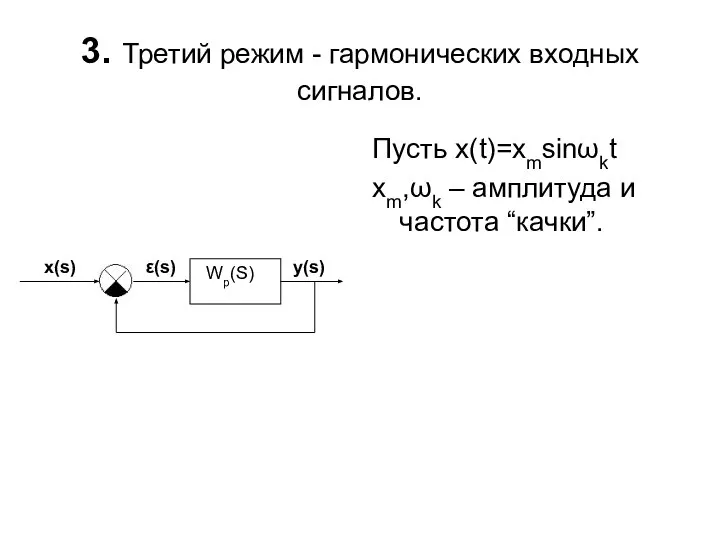
- 17. 3. Третий режим - гармонических входных сигналов. Пусть x(t)=xmsinωkt xm,ωk – амплитуда и частота “качки”. Wp(S)
- 18. Определим амплитуду εm ошибки САУ в этом режиме. Для этого найдем: - ПФ САУ по ошибке
- 19. Выражение (1) справедливо и для амплитуд, т.е. Откуда следует: (2) Прологарифмируем (2): (3) Ак – контрольная
- 20. Из (3) следует, что САУ будет иметь амплитуду ошибки не более допустимой εдоп, если Из (3)
- 21. Т.о. чтобы ошибка САУ в гармоническом режиме не превышала допустимой εдоп необходимо: 1. Определить положение контрольной
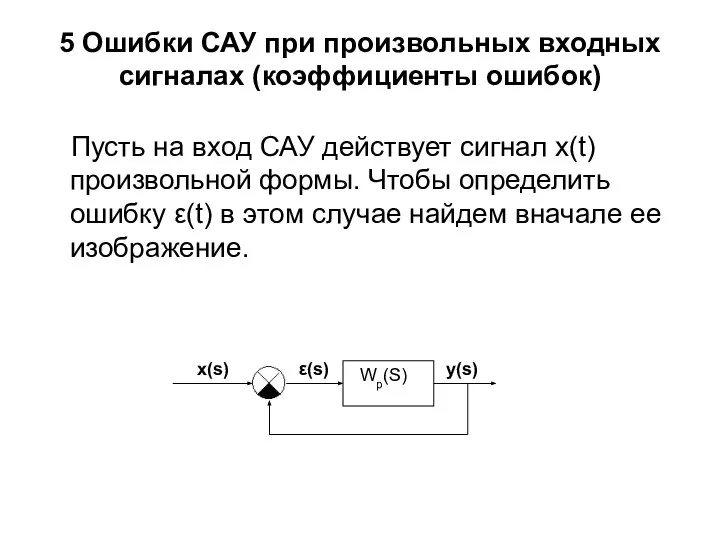
- 22. 5 Ошибки САУ при произвольных входных сигналах (коэффициенты ошибок) Пусть на вход САУ действует сигнал x(t)
- 23. Поскольку: (1) То: (2) Разложим далее Fε(s) по возрастающим степеням S в ряд, тогда (2) можно
- 24. При нулевых начальных условиях и переходя в (3) к оригиналам можно записать (4) Величины С0, С1,
- 25. Чтобы определить ошибку САУ при произвольной форме входного сигнала x(t) необходимо: Определить передаточную функцию САУ по
- 26. Пример Найти ошибку в САУ при: Если:
- 27. Решение: 1.Найдем
- 28. 2. Разложим (1) в степенной ряд путем деления числителя на знаменатель - -
- 29. Ограничимся первыми тремя членами ряда, т.к. входной сигнал X(t) имеет лишь три не нулевых первых производных.
- 30. 3. Итак: (5) Сопоставляя (5) и (4) имеем коэффициенты ошибок: С0=0 (6)
- 31. 4. Определим далее производные от X(t): (7)
- 32. 5. Подставляя коэффициенты С0, С1, С2… и производные (7) в (4) получим: Т.е. ошибка с течением
- 33. 6 Методы повышения точности САУ Анализируя выражения для коэффициентов ошибок отметим, что: Все коэффициенты обратно-пропорциональны коэффициенту
- 34. ВНИМАНИЕ Порядок астатизма “v” определяется числом интегрирующих звеньев в контуре системы. Формально “v” равно показателю степени
- 35. 1. Первый способ повышения точности САУ – увеличение К Т.о. самым универсальным способом повышения точности САУ
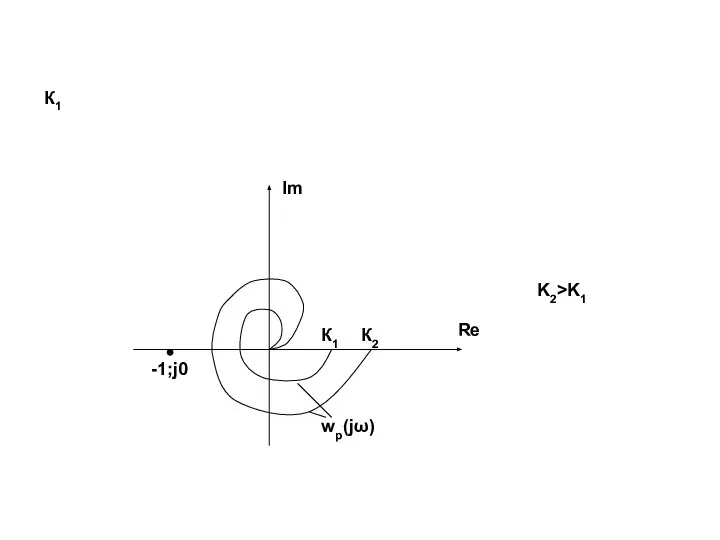
- 36. К1
- 37. 2. Способ повышения точности САУ – путем увеличения астатизма “v” v=0 (статическая САУ) Все коэффициенты не
- 38. v=1 (астатическая САУ с астатизмом первого порядка) v=2 (астатическая САУ с астатизмом второго порядка) с0=0 с1≠0
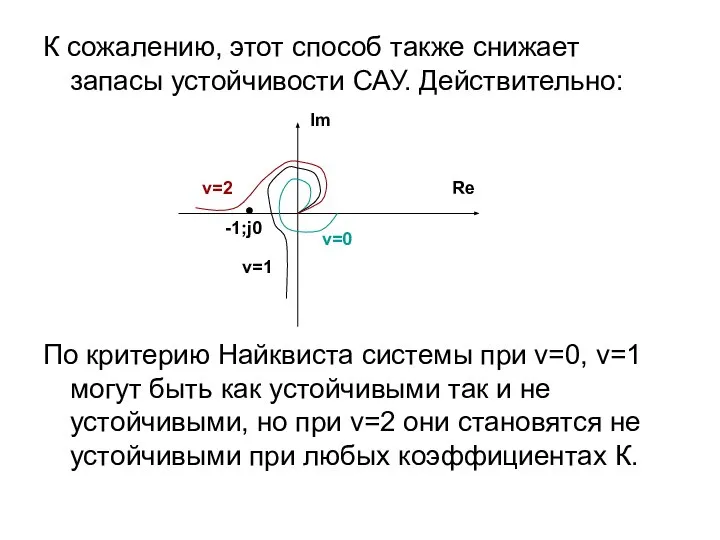
- 39. К сожалению, этот способ также снижает запасы устойчивости САУ. Действительно: По критерию Найквиста системы при v=0,
- 40. 3. Повышение точности САУ с использованием принципов комбинированного управления. Принцип комбинированного управления состоит в том, что
- 41. Здесь сочетается (комбинируются) оба названных принципа: Управление по возмущению (за счет измерения возмущения v(t) и выработки
- 42. Wэ(S) Рассмотрим следящую систему с комбинированным управлением и найдем передаточную функцию обычной системы эквивалентной по точности.
- 43. Для этого приравняем их передаточные функции. (1)
- 44. Из (1) после некоторых преобразований можно получить: (2) Как видно из последнего выражения, при: (3) wэ(s)=∞
- 45. Это означает, что ошибка рассматриваемой комбинированной следящей системы будет равна 0 в любых режимах работы поскольку:
- 46. Достоинство принципа комбинированного управления в том, что он не изменяет (не ухудшает) устойчивости и качества переходных
- 47. ПРИМЕР Пусть: Найдем:
- 48. y(s) Структурная схема такой комбинированной следящей системы имеет вид: y(s) w1(s) x(s) III II I
- 50. Скачать презентацию











































 Функция
Функция Схемы замещения трансформаторов и автотрансформаторов
Схемы замещения трансформаторов и автотрансформаторов Метод наименьших квадратов
Метод наименьших квадратов  Подбор отопительных приборов. Практика 6
Подбор отопительных приборов. Практика 6 Ковровые изделия
Ковровые изделия Не расточая лишних слов, Я вам дарю букет цветов. Желаю быть прекрасным дамам Ещё прекраснее - с цветами! Для Вас сегодня солнце свет
Не расточая лишних слов, Я вам дарю букет цветов. Желаю быть прекрасным дамам Ещё прекраснее - с цветами! Для Вас сегодня солнце свет Теории глобализации и регионализации с точки зрения их соответствия или противоречия с существующими интеграционными группировк
Теории глобализации и регионализации с точки зрения их соответствия или противоречия с существующими интеграционными группировк Указательные слова с сложноподчинённом предложении.
Указательные слова с сложноподчинённом предложении. ФАЗОВЫЕ превращения
ФАЗОВЫЕ превращения Коми. Народное искусство
Коми. Народное искусство Traditional Festival in China The new year eve and Spring Festival
Traditional Festival in China The new year eve and Spring Festival Ответственность субъектов предпринимательской деятельности. Лекция 9
Ответственность субъектов предпринимательской деятельности. Лекция 9 Презентация "Христианская семья и ее ценности" - скачать презентации по МХК
Презентация "Христианская семья и ее ценности" - скачать презентации по МХК Угадай мультик
Угадай мультик Игры с кругами Луллия (Технология ТРИЗ)
Игры с кругами Луллия (Технология ТРИЗ) Никогда не сдавайся!
Никогда не сдавайся! Методы исследования электрической активности сердца
Методы исследования электрической активности сердца Методика обучения аудированию в 10-11-х классах
Методика обучения аудированию в 10-11-х классах  Карбюраторы двухкамерные
Карбюраторы двухкамерные Глагол
Глагол Сөз мәдинеті. Сөйлеу мәдениеті-ел мәртебесі
Сөз мәдинеті. Сөйлеу мәдениеті-ел мәртебесі Time’s up a the elektronika
Time’s up a the elektronika Дом-музей Элиаса Лённрота
Дом-музей Элиаса Лённрота Профессиональное самоопределение как средство социализации и адаптации учащихся в современных условиях
Профессиональное самоопределение как средство социализации и адаптации учащихся в современных условиях Программирование. Введение
Программирование. Введение Расчет суммы страхового возмещения по личному страхованию
Расчет суммы страхового возмещения по личному страхованию  Физиология вегетативной нервной системы (ВНС) ВНС – часть общей нервной системы, которая регулирует вегетативные (растительны
Физиология вегетативной нервной системы (ВНС) ВНС – часть общей нервной системы, которая регулирует вегетативные (растительны СЕБЕСТОИМОСТЬ ПРОДУКЦИИ
СЕБЕСТОИМОСТЬ ПРОДУКЦИИ