Содержание
- 2. Понятие устойчивости движения
- 4. Первый метод Ляпунова Теорема 1. Если линейная система первого приближения устойчива, то соответствующее состояние равновесия нелинейной
- 5. Второй метод Ляпунова Ляпунов вводит в рассмотрение специальную функцию V(y1,y2,....,yn), со следующими свойствами: 1. Функция V(y1,y2,....,yn)
- 6. ЗНАКООПРЕДЕЛЕННЫЕ ФУНКЦИИ Функция V - знакоопределенная, если во всех точках вокруг начала координат она сохраняет один
- 7. ЗНАКОПОСТОЯННЫЕ И ЗНАКОПЕРЕМЕННЫЕ ФУНКЦИИ Функция V - знакопостоянна, если сохраняет один и тот же знак, но
- 8. Теоремы Ляпунова Теорема 1. Если существует знакоопределенная функция производная которой по времени dV/dt, тоже знакоопределенная (или
- 9. Построение функции Ляпунова ПРИ ПРАКТИЧЕСКОМ ИСПОЛЬЗОВАНИИ ВТОРОГО МЕТОДА ЛЯПУНОВА ОДНОЙ ИЗ ОСНОВНЫХ ПРОБЛЕМ ЯВЛЯЕТСЯ ВЫБОР ФУНКЦИИ
- 10. Пример. Исследовать устойчивость системы, заданной уравнениями: Это достаточное условие устойчивости исследуемой нелинейной системы. Границей устойчивости системы
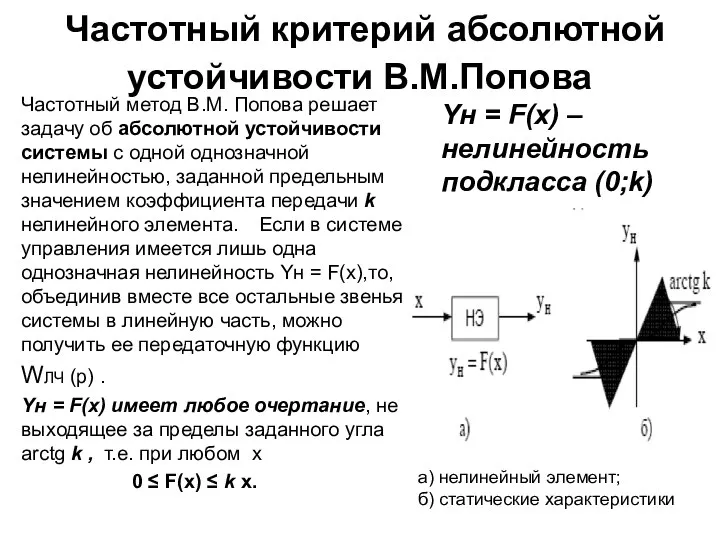
- 11. Частотный критерий абсолютной устойчивости В.М.Попова Частотный метод В.М. Попова решает задачу об абсолютной устойчивости системы с
- 12. Теорема В.М. Попова Для установления абсолютной устойчивости нелинейной системы достаточно подобрать такое конечное действительное число q,
- 13. Введем видоизмененную частотную характеристику линейной части системы W*(j ω) , которая определяется : где: T0 =
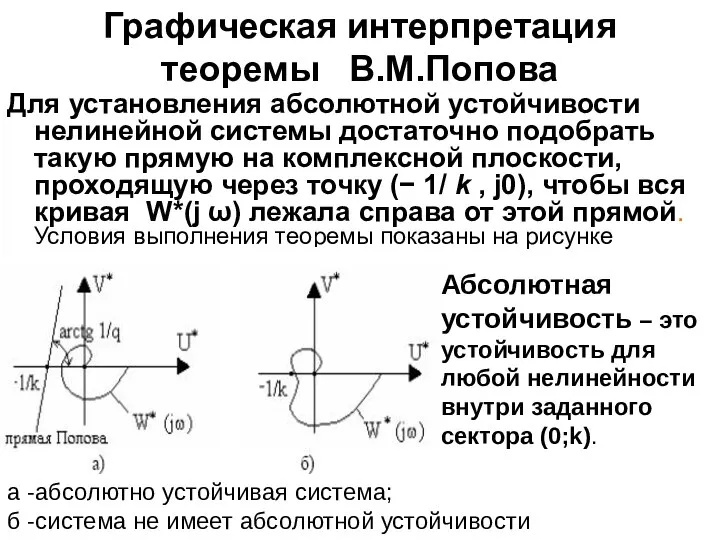
- 14. Графическая интерпретация теоремы В.М.Попова Для установления абсолютной устойчивости нелинейной системы достаточно подобрать такую прямую на комплексной
- 15. Правило применения критерия Попова 1. На комплексной плоскости строим модифицированный годограф W*(j ω). 2. Отмечаем точку
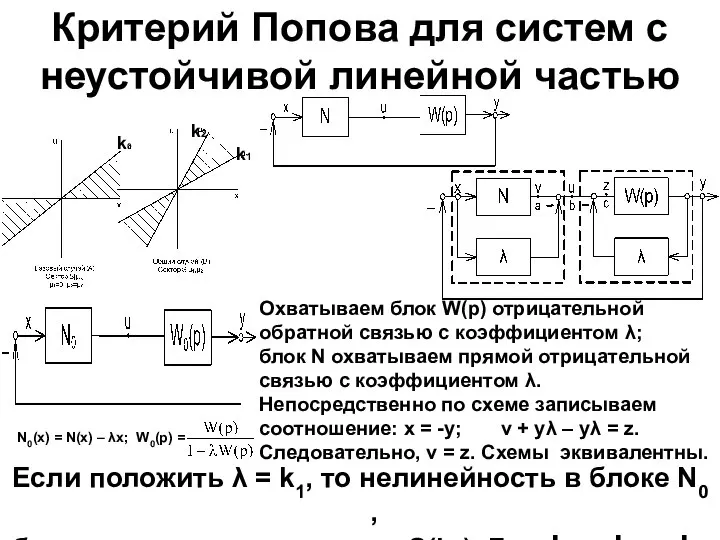
- 16. Критерий Попова для систем с неустойчивой линейной частью N0(x) = N(x) – λx; W0(p) = k0
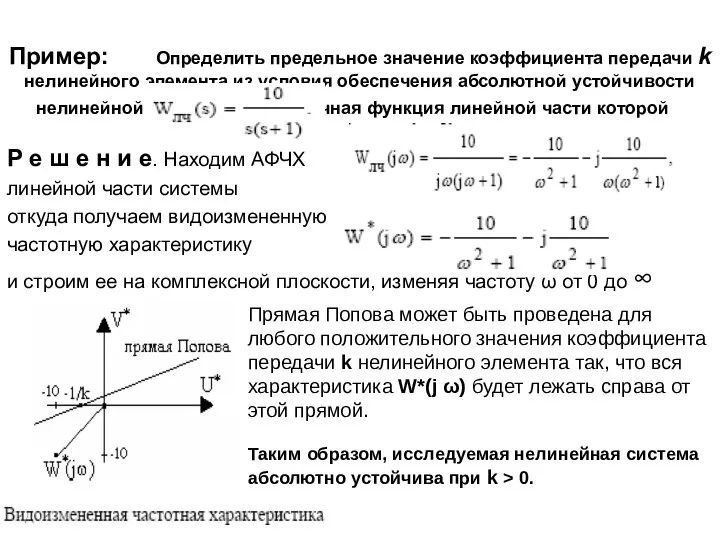
- 17. Пример: Определить предельное значение коэффициента передачи k нелинейного элемента из условия обеспечения абсолютной устойчивости нелинейной системы,
- 18. Тренировочное задание
- 19. Тренировочное задание А. Какое движение называется возмущенным движением и какое движение называется невозмущенным движением? В. Какой
- 20. Тренировочное задание А.Какая теорема физики лежит в основе второго метода Ляпунова? В. Какими свойствами должна обладать
- 21. Тренировочное задание А. Как Вы понимаете абсолютную устойчивость? В. Что представляет собой видоизмененная амплитудно-фазовая характеристика линейной
- 22. Тренировочное задание
- 24. Скачать презентацию

















 Презентация "Искусство как специфическая форма познания мира" - скачать презентации по МХК
Презентация "Искусство как специфическая форма познания мира" - скачать презентации по МХК РОССИЯ Родина моя
РОССИЯ Родина моя  Судебная система Российской Федерации: Мировые судьи
Судебная система Российской Федерации: Мировые судьи В городе богини Афины
В городе богини Афины Презентация Основные современные источники научной информации
Презентация Основные современные источники научной информации Презентация на тему "Новый год" - скачать презентации по Педагогике
Презентация на тему "Новый год" - скачать презентации по Педагогике Суженый-ряженый (программа мероприятия)
Суженый-ряженый (программа мероприятия) Народные символы и обереги
Народные символы и обереги Вирусный гепатит диагностика
Вирусный гепатит диагностика  Следственный комитет РФ
Следственный комитет РФ Гигиеническая оценка условий водораспределения
Гигиеническая оценка условий водораспределения  Новая Концепция Таможенного регулирования Внешне экономической деятельности Майстренко Денис Т-115
Новая Концепция Таможенного регулирования Внешне экономической деятельности Майстренко Денис Т-115 Организация производственной деятельности на станциях технического обслуживания автомобилей (тема 1)
Организация производственной деятельности на станциях технического обслуживания автомобилей (тема 1) Объектно-ориентированное программирование. Наследование
Объектно-ориентированное программирование. Наследование Разъемные и неразъемные соединения. Изображение соединений деталей
Разъемные и неразъемные соединения. Изображение соединений деталей Международные отношения в 20-30-е годы XX века
Международные отношения в 20-30-е годы XX века  Питание в пауэрлифтинге
Питание в пауэрлифтинге Авиация таможенных органов Подготовил студент: Косолапов Алексей Группа: Т-102 Дисциплина: История Таможенного дела
Авиация таможенных органов Подготовил студент: Косолапов Алексей Группа: Т-102 Дисциплина: История Таможенного дела Тригонометрические уравнения Обобщающий урок
Тригонометрические уравнения Обобщающий урок Средства при нарушении мозгового кровообращения
Средства при нарушении мозгового кровообращения Канада
Канада Роль распределительной компьютерной инфраструктуры
Роль распределительной компьютерной инфраструктуры  Материал для изготовления мебели. Древесноволокнистая плита (ДВП
Материал для изготовления мебели. Древесноволокнистая плита (ДВП Автоматическая система водоохлаждения на АЭС
Автоматическая система водоохлаждения на АЭС Налогообложение на выбросы СО2
Налогообложение на выбросы СО2 Способы преобразования чертежа
Способы преобразования чертежа Пример планового техобслуживания автомобиля (1 пост / 1 механик). Задачи планового техобслуживания
Пример планового техобслуживания автомобиля (1 пост / 1 механик). Задачи планового техобслуживания Сдвигающий регистр многотактного действия
Сдвигающий регистр многотактного действия