Содержание
- 2. 10. ТЕОРИЯ ДВОЙСТВЕННОСТИ 10.1. Постановка двойственной задачи. 10.2. Теорема двойственности.
- 3. 10.1. Постановка двойственной задачи. определенную формулой Нетрудно видеть, что неравенство переходит в равенство. Отсюда выводим равенство
- 4. Тогда исходную задачу можно переписать в виде. Задача 1. и сконструируем задачу. Задача 2. Определение 1.
- 5. 10.2. Теорема двойственности. основной и двойственной задач. Теорема 1. Имеет место неравенство Доказательство. от обеих частей
- 6. Теорема доказана. Теорема 2 (двойственности). Для того чтобы было выполнено необходимо и достаточно, Множество седловых точек
- 7. Последнее равенство означает, что Отсюда также следует, вложено в множество седловых точек функции Лагранжа. Достаточность. седловая
- 8. выводим Из (7),(6) в силу теоремы 1 получим Тогда Отсюда выводим, что множество седловых точек функции
- 9. также являются седловыми точками. можно выбирать одними и теми же Тогда множители Лагранжа в теореме Куна
- 10. Пример 1. Пусть Данная функция имеет единственную седловую точку а Существуют задачи выпуклого программирования, даже если
- 11. Выпишем функцию Лагранжа для данной задачи Вычисляем Пояснения требует третья строчка в равенстве (8). Приведем график
- 12. Отсюда и соотношение (8) доказано. Таким образом, но
- 13. Двойственная задача всегда является задачей выпуклого программирования какой была основная (исходная) задача. Действительно, двойственная задача эквивалентна
- 15. Двойственная задача к двойственной не обязана совпадать с исходной задачей. Например, если исходная задача не является
- 17. Скачать презентацию














 2018 FIFA World Cup Russia
2018 FIFA World Cup Russia СИСТЕМА АККРЕДИТАЦИИ РЕСПУБЛИКИ БЕЛАРУСЬ
СИСТЕМА АККРЕДИТАЦИИ РЕСПУБЛИКИ БЕЛАРУСЬ Экономика и особенности деятельности отраслей культуры
Экономика и особенности деятельности отраслей культуры Презентация Сущность организации, их типология, организация
Презентация Сущность организации, их типология, организация Основи будови військових засобів вимірювань. Засоби вимірювань
Основи будови військових засобів вимірювань. Засоби вимірювань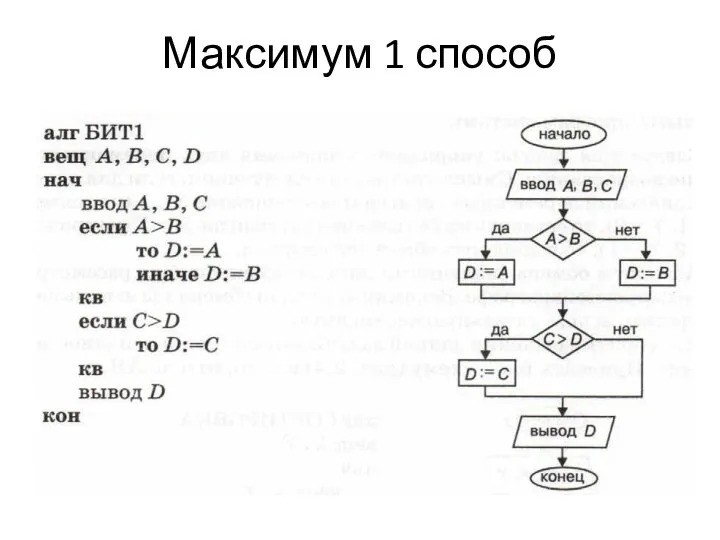 Минимум, максимум, разница и сумма
Минимум, максимум, разница и сумма Презентация "Доходы и расходы семьи. Стоимость жизни" - скачать презентации по Экономике
Презентация "Доходы и расходы семьи. Стоимость жизни" - скачать презентации по Экономике Информационные технологии в экономике Презентацию подготовил студент группы Э-14-2 Лутов Олег
Информационные технологии в экономике Презентацию подготовил студент группы Э-14-2 Лутов Олег Un chatton
Un chatton Подпрограммы. Определение функции, фактические и формальные параметры функции
Подпрограммы. Определение функции, фактические и формальные параметры функции Презентация
Презентация  Средняя общеобразовательная школа 10 с углубленным изучением отдельных предметов г. Марганец, 2011 год. Презентация опыта работы учи
Средняя общеобразовательная школа 10 с углубленным изучением отдельных предметов г. Марганец, 2011 год. Презентация опыта работы учи Структура спортивно-педагогической деятельности
Структура спортивно-педагогической деятельности Физиологическая классификация и характеристика физических упражнений
Физиологическая классификация и характеристика физических упражнений Темы про Пететрбург и Москву
Темы про Пететрбург и Москву Бизнес Сервис Центр Харьков. Инструкция по выставлению осуществленных рейсов ТЭК на оплату (блок документы)
Бизнес Сервис Центр Харьков. Инструкция по выставлению осуществленных рейсов ТЭК на оплату (блок документы) 2 класс СЛОВАРНЫЕ СЛОВА Г, Д, З УМК «Школа России» Выполнила: Олифиренко Елена Александровна, учитель начальных классов МОУ-СО
2 класс СЛОВАРНЫЕ СЛОВА Г, Д, З УМК «Школа России» Выполнила: Олифиренко Елена Александровна, учитель начальных классов МОУ-СО Социальная инженерия
Социальная инженерия Презентация на тему "Использование информационно-коммуникационных технологий в начальной школе" - скачать презентации по Пе
Презентация на тему "Использование информационно-коммуникационных технологий в начальной школе" - скачать презентации по Пе Презентация Диалектика как учение о развитии
Презентация Диалектика как учение о развитии Barranquismo
Barranquismo Открытия. Деловой стиль в одежде
Открытия. Деловой стиль в одежде Малярные работы и контроль качества малярных работ
Малярные работы и контроль качества малярных работ Система процессов деятельности таможни
Система процессов деятельности таможни  Поклонение и Субботняя школа. Качество служений
Поклонение и Субботняя школа. Качество служений Los juegos olimpicos de rio 2016
Los juegos olimpicos de rio 2016 Социология и политология как науки
Социология и политология как науки Перспективы использования идентификационных номеров и защитных знаков
Перспективы использования идентификационных номеров и защитных знаков