Свободное движение твердого тела
Свободно движущееся тело всегда вращается вокруг коси, проходящей
через центр масс тела (не обязательно главной)
Оси вращения несимметричных тел, как правило, не устойчивы.
При наличии внешних сил (даже слабых) ось вращения может менять направление, а при вращении тела вокруг закрепленной оси на оси могут возникать заметные нагрузки. Если убрать закрепление - тело может начать «кувыркаться».
У симметричных тел могут быть т.н. главные оси симметрии, вращение вокруг которых может быть устойчиво.
«Самые главные» оси те, вращение вокруг которых всегда устойчиво. Такое вращение может продолжаться даже после снятия закрепления.
Пример: быстрое вращение стержня на подвесе остается устойчивым еще некоторое время, если снять нить с подвеса. По мере замедления вращения устойчивость его теряется.










 Распределение газовых молекул по скоростям и энергиям (Тема 2)
Распределение газовых молекул по скоростям и энергиям (Тема 2) Первое начало термодинамики
Первое начало термодинамики Оптика. Лазеры
Оптика. Лазеры Диагностика ходовой части и рулевого управления
Диагностика ходовой части и рулевого управления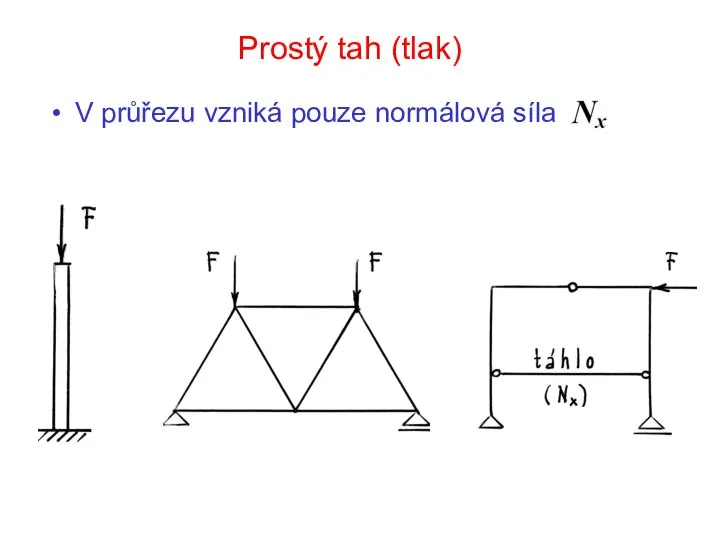 Prostý tah (tlak)
Prostý tah (tlak) Гамма-излучение
Гамма-излучение Презентация по физике "Преломление света" - скачать бесплатно
Презентация по физике "Преломление света" - скачать бесплатно Матроиды структуры токов и напряжений
Матроиды структуры токов и напряжений Конструкциялық материалдардың беріктік және созымдылық физикасы
Конструкциялық материалдардың беріктік және созымдылық физикасы Представление аналогового сигнала в дискретной форме
Представление аналогового сигнала в дискретной форме Подготовил ученик 8 «А» класса МОУ СОШ № 7 г.о.Новокуйбышевска Самарская область Шлыков Влад. «Исследование электромагнитного из
Подготовил ученик 8 «А» класса МОУ СОШ № 7 г.о.Новокуйбышевска Самарская область Шлыков Влад. «Исследование электромагнитного из Теоретическая (техническая) механика. Статика
Теоретическая (техническая) механика. Статика Что изучает физика. Физические термины
Что изучает физика. Физические термины Система кондиционирования воздуха
Система кондиционирования воздуха Оптические приборы
Оптические приборы История паровых машин
История паровых машин Настройка автомодели для дрифтинга
Настройка автомодели для дрифтинга Атомные электростанции
Атомные электростанции Плоская система произвольно расположенных сил. Статика
Плоская система произвольно расположенных сил. Статика Урок физики в 7 классе Коваленко МГ
Урок физики в 7 классе Коваленко МГ Влияние радиоактивных излучений на живые организмы
Влияние радиоактивных излучений на живые организмы Импульс тела. Закон сохранения импульса. Причины введения импульса
Импульс тела. Закон сохранения импульса. Причины введения импульса Магнитооптика ферромагнетиков
Магнитооптика ферромагнетиков Основные постулаты квантовой теории
Основные постулаты квантовой теории Міцносні характеристики ґрунту. Умова міцності в точці ґрунтового масиву. (Лекція 7)
Міцносні характеристики ґрунту. Умова міцності в точці ґрунтового масиву. (Лекція 7) Спектры . спектральный анализ. Спектральные аппараты
Спектры . спектральный анализ. Спектральные аппараты Выпускная квалификационная работа: Система термостатирования тканей человека
Выпускная квалификационная работа: Система термостатирования тканей человека Измерение объема тела
Измерение объема тела