Содержание
- 2. 02/21/02 (c) 2001 University of Wisconsin, CS559 Today Viewing Orthographic viewing Homework 3
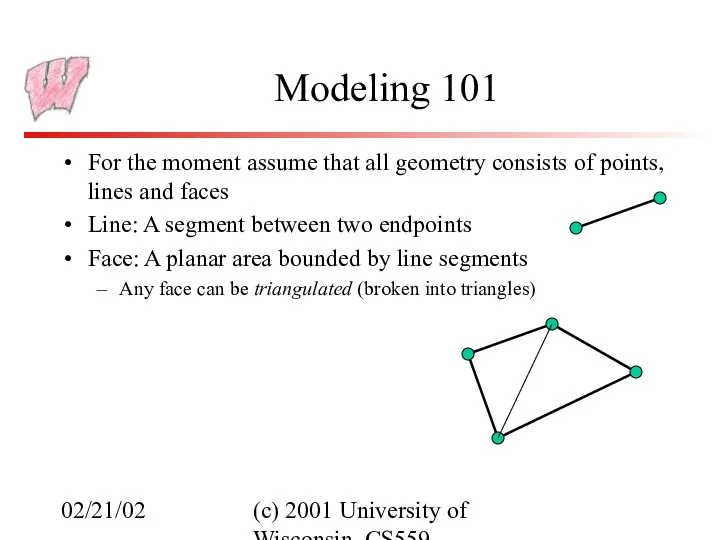
- 3. 02/21/02 (c) 2001 University of Wisconsin, CS559 Modeling 101 For the moment assume that all geometry
- 4. 02/21/02 (c) 2001 University of Wisconsin, CS559 Modeling and OpenGL In OpenGL, all geometry is specified
- 5. 02/21/02 (c) 2001 University of Wisconsin, CS559 Rendering Generate an image showing the contents of some
- 6. 02/21/02 (c) 2001 University of Wisconsin, CS559 Graphics Pipeline Graphics hardware employs a sequence of coordinate
- 7. 02/21/02 (c) 2001 University of Wisconsin, CS559 Local Coordinate Space It is easiest to define individual
- 8. 02/21/02 (c) 2001 University of Wisconsin, CS559 Global Coordinate System Everything in the world is transformed
- 9. 02/21/02 (c) 2001 University of Wisconsin, CS559 View Space Associate a set of axes with the
- 10. 02/21/02 (c) 2001 University of Wisconsin, CS559 3D Screen Space Transform view space into a cube:
- 11. 02/21/02 (c) 2001 University of Wisconsin, CS559 Window Space Also called screen space (confusing) Convert the
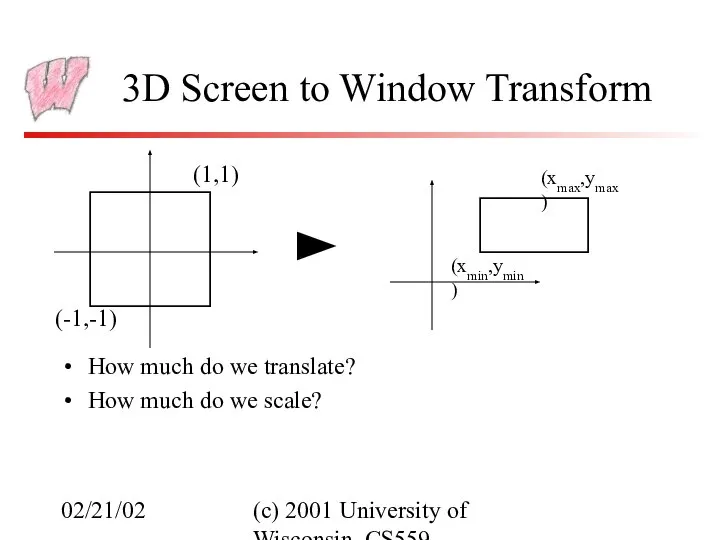
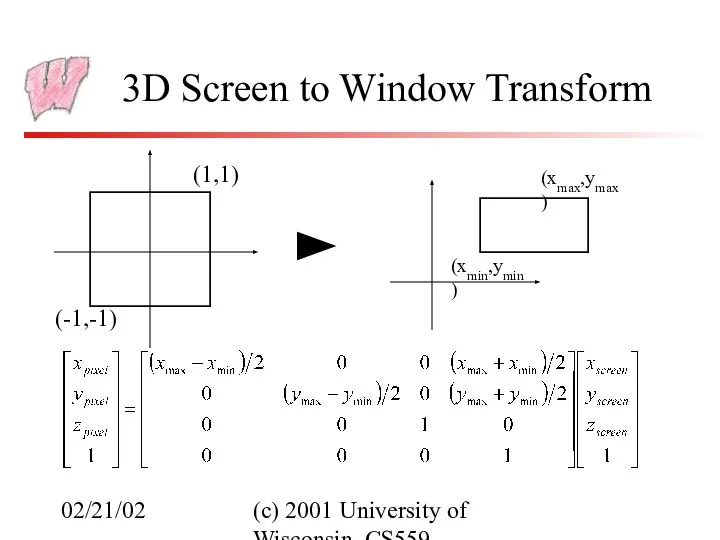
- 12. 02/21/02 (c) 2001 University of Wisconsin, CS559 3D Screen to Window Transform Typically, windows are specified
- 13. 02/21/02 (c) 2001 University of Wisconsin, CS559 3D Screen to Window Transform How much do we
- 14. 02/21/02 (c) 2001 University of Wisconsin, CS559 3D Screen to Window Transform (-1,-1) (1,1) (xmin,ymin) (xmax,ymax)
- 15. 02/21/02 (c) 2001 University of Wisconsin, CS559 Orthographic Projection Orthographic projection projects all the points in
- 16. 02/21/02 (c) 2001 University of Wisconsin, CS559 Simple Orthographic Projection Specify the region of space that
- 17. 02/21/02 (c) 2001 University of Wisconsin, CS559 Rendering the Volume To project, map the view volume
- 18. 02/21/02 (c) 2001 University of Wisconsin, CS559 General Orthographic Projection We could look at the world
- 19. 02/21/02 (c) 2001 University of Wisconsin, CS559 Specifying a View The location of the image plane
- 20. 02/21/02 (c) 2001 University of Wisconsin, CS559 Getting there… We wish to end up in the
- 21. 02/21/02 (c) 2001 University of Wisconsin, CS559 View Space Given our camera definition: Which point is
- 22. 02/21/02 (c) 2001 University of Wisconsin, CS559 View Space The origin is at the center of
- 23. 02/21/02 (c) 2001 University of Wisconsin, CS559 World to View We must translate the world so
- 24. 02/21/02 (c) 2001 University of Wisconsin, CS559 All Together We apply a translation and then a
- 25. 02/21/02 (c) 2001 University of Wisconsin, CS559 OpenGL and Transformations OpenGL internally stores several matrices that
- 26. 02/21/02 (c) 2001 University of Wisconsin, CS559 OpenGL Camera The default OpenGL image plane has u
- 28. Скачать презентацию






















 Закон всемирного тяготения
Закон всемирного тяготения Кинематические точки
Кинематические точки Расчет криволинейных стержней
Расчет криволинейных стержней Паровая машина Ивана Ползунова
Паровая машина Ивана Ползунова Законы преломления.
Законы преломления. Нестационарная теплопроводность цилиндра конечных размеров
Нестационарная теплопроводность цилиндра конечных размеров Работа и мощность электрического тока
Работа и мощность электрического тока Электрический ток
Электрический ток Презентация по физике "Системы цветопередачи" - скачать
Презентация по физике "Системы цветопередачи" - скачать  Ритм
Ритм Система с использованием ПИД-регулятора для задачи следования по линии
Система с использованием ПИД-регулятора для задачи следования по линии Физические основы действия ионизирующего излучения
Физические основы действия ионизирующего излучения Линзы. Виды
Линзы. Виды Электромагниты (8 класс)
Электромагниты (8 класс) Брейн - ринг. Физика
Брейн - ринг. Физика Двигуни внутрішнього згорання Підготувала учениця 10-Ф класу, Семененко Анна
Двигуни внутрішнього згорання Підготувала учениця 10-Ф класу, Семененко Анна  Презентация по физике "Динамическая теория дифракции рентгеновских лучей в кристаллах" - скачать бесплатно
Презентация по физике "Динамическая теория дифракции рентгеновских лучей в кристаллах" - скачать бесплатно Поперечность световых волн. Поляризация света
Поперечность световых волн. Поляризация света Искровой разряд Презентацию подготовили ученики 9-Б класса ХСШ №16 Поваляев Игорь и Калайтан Владислав
Искровой разряд Презентацию подготовили ученики 9-Б класса ХСШ №16 Поваляев Игорь и Калайтан Владислав  Потенциальные кривые и условие равновесия механических систем
Потенциальные кривые и условие равновесия механических систем Механические колебания и волны. Акустика
Механические колебания и волны. Акустика Уровнемеры и датчики положения
Уровнемеры и датчики положения Термодинамическая картина мира
Термодинамическая картина мира Неразличимость частиц. Симметрия
Неразличимость частиц. Симметрия Получение и применение кристаллов
Получение и применение кристаллов  Проводники и диэлектрики в электростатическом поле
Проводники и диэлектрики в электростатическом поле Атомная физика
Атомная физика Араластыру әдістері. Пневматикалық араластыру
Араластыру әдістері. Пневматикалық араластыру