Содержание
- 2. Лекция 8 Механика твердого тела Лектор: доцент НИЯУ МИФИ, к.ф.-м.н., Ольчак Андрей Станиславович Общая Физика
- 3. Механика твердого тела Вращательное движение Момент импульса. (повторение) Механика твердого тела
- 4. 1. Поступательное движение Поступательное движение - такое движение твердого тела, при котором любая прямая проведенная между
- 5. 1. Поступательное движение Поступательное движение твердого тела: любая прямая проведенная между любыми двумя точками твердого тела
- 6. 2. Вращение твердого тела вокруг неподвижной оси При вращении твердого тела вокруг закрепленной оси все его
- 7. Вращательное движение характеризуется угловой скоростью: ω = dφ/dt [с-1 ] угловая скорость – (псевдо)вектор, направленный вдоль
- 8. Момент импульса Производная по времени момента импульса частицы относительно некоторой точки равна моменту силы относительно той
- 9. Закон сохранения момента импульса При отсутствии внешних сил Для замкнутой системы момент импульса постоянен Момент импульса
- 10. Механика твердого тела
- 11. Момент импульса твердого тела при вращении вокруг неподвижной оси Момент импульса элементарной массы mi относительно оси
- 12. Уравнение движения для вращающегося твердого тела Это уравнение является аналогом второго закона Ньютона для поступательного движения.
- 13. Моменты инерции для некоторых симметричных тел Момент инерции твердого тела относительно оси вращения OZ можно представить
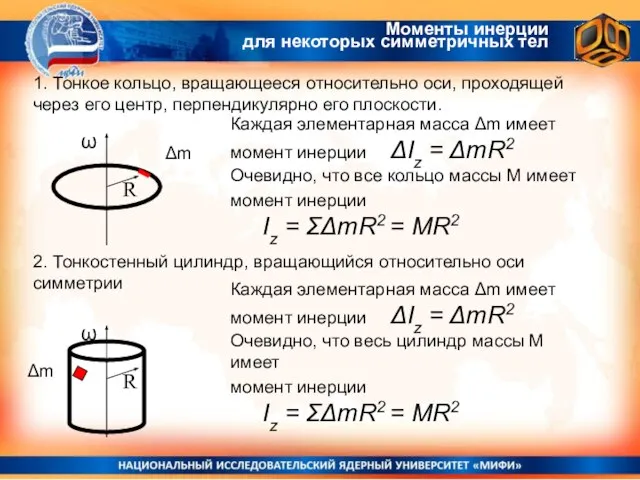
- 14. Моменты инерции для некоторых симметричных тел 1. Тонкое кольцо, вращающееся относительно оси, проходящей через его центр,
- 15. Моменты инерции для некоторых симметричных тел 3. Однородный цилиндр с плотностью вещества ρ, вращающийся вокруг оси
- 16. Моменты инерции для некоторых симметричных тел 4. Тонкостенная сфера массы М и радиуса R, вращаю- щаяся
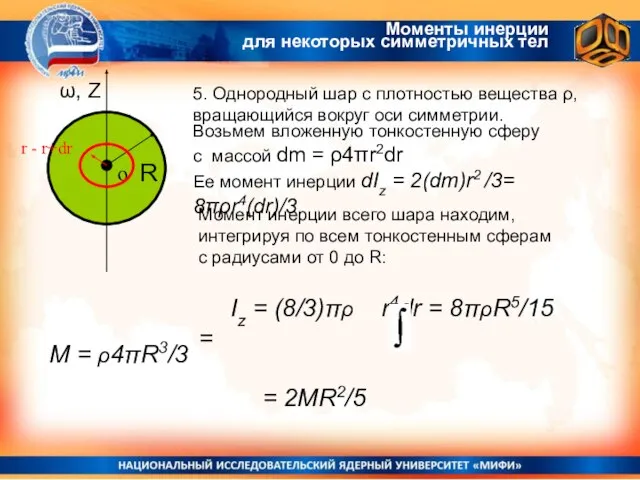
- 17. Моменты инерции для некоторых симметричных тел 5. Однородный шар с плотностью вещества ρ, вращающийся вокруг оси
- 18. Моменты инерции для некоторых симметричных тел 6. Однородный тонкий стержень длины и массы М, вращающийся вокруг
- 19. Моменты инерции для некоторых симметричных тел 1. Материальная точка, вращающаяся вокруг оси на расстоянии R от
- 20. Теорема Штайнера o C mi Ri Rci a Пусть нам известен момент инерции тела массы М
- 21. Кинетическая энергия твердого тела при вращении вокруг неподвижной оси Окончательно для кинетической энергии находим: T =
- 22. Работа внешних сил при вращении твердого тела вокруг неподвижной оси fi- равнодействующая всех внутренних сил, действующих
- 25. Скачать презентацию





![Вращательное движение характеризуется угловой скоростью: ω = dφ/dt [с-1 ] угловая](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/616977/slide-6.jpg)














 Теорема Гаусса
Теорема Гаусса Лампы накаливания
Лампы накаливания Методы травления материалов электронной техники
Методы травления материалов электронной техники Презентация ИСПАРЕНИЕ 8 класс
Презентация ИСПАРЕНИЕ 8 класс  Магнитное поле и его свойства
Магнитное поле и его свойства ИСТОРИЯ ОТКРЫТИЯ РАДИОАКТИВНОСТИ Н.М.Вострикова МОУ СОШ № 62, Центральный район, г. Воронеж
ИСТОРИЯ ОТКРЫТИЯ РАДИОАКТИВНОСТИ Н.М.Вострикова МОУ СОШ № 62, Центральный район, г. Воронеж Презентация шкала электромагнитных излучении
Презентация шкала электромагнитных излучении Презентация по физике Законы Ньютона
Презентация по физике Законы Ньютона  Механизмы релаксации напряженно-деформированного состояния металла деталей машин. Модели вязко-хрупкого перехода
Механизмы релаксации напряженно-деформированного состояния металла деталей машин. Модели вязко-хрупкого перехода Линзы. Собирающие и рассеивающие линзы
Линзы. Собирающие и рассеивающие линзы Электризация тел
Электризация тел Расчет определения коэффициента усиления
Расчет определения коэффициента усиления Основы термической обработки металлов и сплавов
Основы термической обработки металлов и сплавов Ядра и частицы
Ядра и частицы Физический диктант по теме: «Магнитное поле»
Физический диктант по теме: «Магнитное поле» Урок по физике в 9 классе Подготовил учитель физики МОУ лицея №5 Терехова Наталья Николаевна 2008г.
Урок по физике в 9 классе Подготовил учитель физики МОУ лицея №5 Терехова Наталья Николаевна 2008г. Давление. Единицы давления
Давление. Единицы давления Колебания систем с одной степенью свободы
Колебания систем с одной степенью свободы Одноканальная аппаратура тонального телеграфирования. Тракт передачи и приема аппаратуры. (Тема 8.2)
Одноканальная аппаратура тонального телеграфирования. Тракт передачи и приема аппаратуры. (Тема 8.2) Радиоактивность. Модели атомов
Радиоактивность. Модели атомов Законы сохранения. Подготовка к ЕГЭ Учитель: Попова И.А. МОУ СОШ № 30 Белово 2010
Законы сохранения. Подготовка к ЕГЭ Учитель: Попова И.А. МОУ СОШ № 30 Белово 2010 Refrigeration Fundamentals. Part 1. Heat and Heat Transfer
Refrigeration Fundamentals. Part 1. Heat and Heat Transfer Сложение взаимно перпендикулярных колебаний
Сложение взаимно перпендикулярных колебаний Магнитное поле
Магнитное поле Ких-фильтры с линейной фчх
Ких-фильтры с линейной фчх ВІльям Томсон
ВІльям Томсон Электрическое поле. Электризация тел (Тест)
Электрическое поле. Электризация тел (Тест) «РЕАКТИВНЫЙ ДВИГАТЕЛЬ»
«РЕАКТИВНЫЙ ДВИГАТЕЛЬ»