Содержание
- 2. § 1. Скалярные и векторные поля. Определение. (скалярного поля). Если в трехмерном пространстве определена функция u(x,y,z),
- 3. Пример. (скалярного поля). Если в начало координат поместить заряд Q, то в каждой точке пространства определена
- 4. Определение. (векторного поля). Говорят, что в трехмерном пространстве задано векторное поле Замечание. В этом случае каждой
- 5. Пример. (поверхности уровня). Если в начало координат поместить заряд Q, то имеем скалярное поле потенциала ,
- 6. Определение. (векторной линии). Пусть в трехмерном пространстве задано векторное поле Векторной линией заданного векторного поля называется
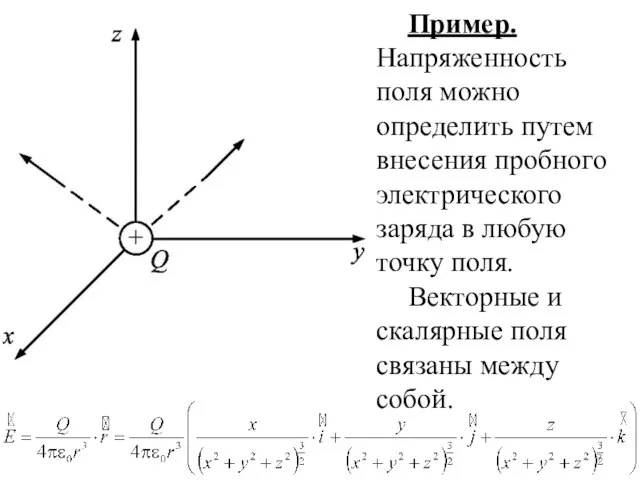
- 7. Пример. Напряженность поля можно определить путем внесения пробного электрического заряда в любую точку поля. Векторные и
- 8. § 2. Производная по направлению. Ее вычисление. Пусть задано скалярное поле u, где u – дифференцируемая
- 9. Df. (производной по направлению): если существует конечный предел отношения приращения скалярного поля к длине вектора, т.е.
- 10. Чтобы вычислить производную по направлению, пользуются теоремой: Th.: (о вычислении производной по направлению). Если скалярное поле
- 11. где α,β,γ − углы определенные в любой точке области V , которые составляет вектор l с
- 12. здесь α1,α2,α3 − бесконечно малые функции в точке М0 , которые стремятся к 0, когда -
- 13. Перейдем к пределу в выражении (2) при Заметим, что Если заменить Δx на Δy и Δx
- 14. Значит, в пределе, учитывая, что α1, α2, α3 → 0 при , имеем: Так как предел
- 15. Что и требовалось доказать. Замечание: Производная скалярного поля по направлению вектора выражает скорость возрастания или убывания
- 16. § 3. Градиент скалярного поля. Связь скалярных и векторных полей. Свойства градиента. Определение. (градиента). Градиентом дифференцируемого
- 17. Определение градиента привязано к декартовой системе координат. Покажем связь скалярных и векторных полей. Пусть задано скалярное
- 18. Вспомним, что скалярное произведение 2-х векторов вычисляется по формуле: Найдем скалярное произведение градиента поля u и
- 19. По этой формуле можно вычислять производную по направлению, зная градиент. Учитывая, что: = проекцияlgradu = Df.
- 20. на произвольное направление вектора равна производной скалярного поля по направлению этого вектора . Свойства градиента: Градиент
- 21. 4. 5. Если задано скалярное поле F(u(x,y,z)), то градиент: gradF(u(x,y,z)) = F′u⋅gradu. § 4. Применение градиента
- 22. Если имеется уравнение поверхности u(x,y,z) = 0, это означает, что задана поверхность уровня скалярного поля u(x,y,z).
- 23. Поток. § 5. Задача, приводящая к понятию потока векторного поля. Пусть в трехмерном пространстве имеется ориентируемая
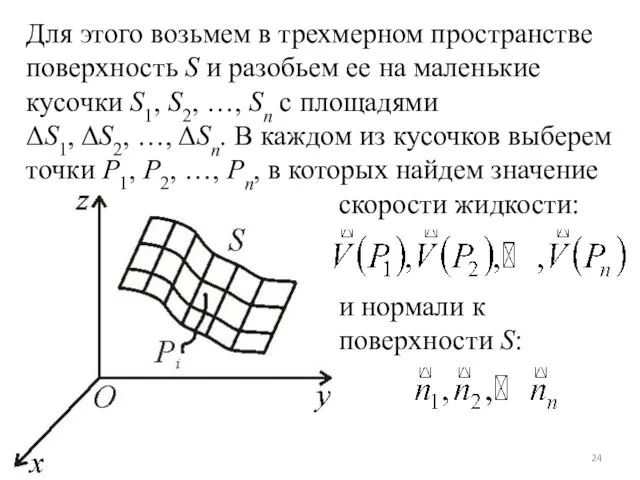
- 24. Для этого возьмем в трехмерном пространстве поверхность S и разобьем ее на маленькие кусочки S1, S2,
- 25. Найдем количество жидкости, которое протекает через участок Si в единицу времени в направлении нормали. Численно это
- 26. Если сложить объемы всех маленьких параллелепипедов, то количество жидкости, протекающее через поверхность S, обозначаемое Q равно:
- 27. то он и будет выражать значение количества жидкости, протекающей через поверхность S. Вспоминая, если предел существует,
- 28. Для того, чтобы количественно описать векторы, электростатического, электромагнитного поля вводится понятие потока. Определение (потока). Потоком векторного
- 29. Примечание: в случае жидкости поток равен количеству жидкости, протекающей через поверхность. § 6. Вычисление потока. Если
- 30. то поток через эту поверхность S может быть вычислен по определению При этом поверхность S должна
- 31. Второй способ вычисления потока называется методом проектирования на координатной плоскости. Чтобы получить формулы, заметим, что нормаль
- 32. Поток через поверхность S равен Пользуясь аддитивностью интеграла
- 33. Предполагая, что поверхность S однозначно проектируется на координатные оси имеем: Поверхностные интегралы 2 рода вычисляются с
- 34. Знаки ± берутся с учетом того, какой угол составляет нормаль к поверхности для 1-го интеграла с
- 35. Пример: пусть дано векторное поле найти поток через внешнюю поверхность конуса S: составляет тупой угол с
- 36. Поток через всю поверхность S:
- 37. § 7. Формула Остроградского. Пусть в трехмерном пространстве задана область V, такая что: Ориентированная внешней нормалью.
- 38. Тогда справедлива формула Остроградского: Поверхность S замкнутая. Доказательство. Самостоятельно. Формула Остроградского применима только в случае замкнутых
- 39. § 8. Векторная запись теоремы Остроградского. Пусть в 3-х мерном пространстве задано векторное поле где P,
- 40. Так как S - замкнутая, гладкая, ориентированная, а функции P, Q, R удовлетворяют условиям теоремы Остроградского,
- 41. Сравнивая правые части формул (1) и (2) и вспоминая что имеем: - векторная запись теоремы Остроградского.
- 42. Пример: Поток векторного поля через поверхность неизвестен. S: нормаль внешняя S - замкнутая поверхность – это
- 43. Замечание: из материала, приведенного выше ясно, что скалярным полям можно поставить в соответствие векторные поля, а
- 44. § 9. Дивергенция векторного поля, ее вычисление. В векторном поле возьмем замкнутую поверхность S с внешней
- 45. В некоторых задачах необходимо знать характеристики векторного поля в каждой точке, независимо от выбора поверхности S.
- 46. Если поверхность S стягивать в точку и предполагать что существует предел такого отношения, то получим плотность
- 47. содержащемся внутри этой поверхности, при стягивании поверхности S в точку, этот предел называется дивергенцией векторного поля
- 48. Теорема. (о вычислении дивергенции) Если в 3-х мерном пространстве задано векторное поле где P, Q, R
- 49. Доказательство: По определению: Так как поверхность S замкнутая, то применяя формулу Остроградского имеем:
- 50. Значит, дивергенция поля может быть записана Частные производные непрерывны, значит к тройному интегралу применима теорема о
- 52. Скачать презентацию















































 Энергия электрического поля
Энергия электрического поля Решение задач по теме Механические движения
Решение задач по теме Механические движения Аттестационная работа. Лабораторная работа Исследование изменения со временем температуры остывающей воды
Аттестационная работа. Лабораторная работа Исследование изменения со временем температуры остывающей воды Закон сохранения и превращения энергии в механических и тепловых процессах.
Закон сохранения и превращения энергии в механических и тепловых процессах. Взаимодействие электронов с веществом. Опыты по рассеянию электронов в газе. АФ1.7
Взаимодействие электронов с веществом. Опыты по рассеянию электронов в газе. АФ1.7 Свободное падение Свободным падением называется движение тел под действием силы тяжести.
Свободное падение Свободным падением называется движение тел под действием силы тяжести. Лазер Выполнил ученик 9А класса МБОУ СОШ № 135 города Казани РТ Загидуллин Кирилл Руководитель учитель физики И.Б.Широкова
Лазер Выполнил ученик 9А класса МБОУ СОШ № 135 города Казани РТ Загидуллин Кирилл Руководитель учитель физики И.Б.Широкова  Электромагнитная совместимость в сетях подвижной радиосвязи
Электромагнитная совместимость в сетях подвижной радиосвязи Лекция 24 (7). Квантовые статистики
Лекция 24 (7). Квантовые статистики Электроизмерительные приборы
Электроизмерительные приборы Презентация по физике "Давление в жидкостях и газе" - скачать бесплатно
Презентация по физике "Давление в жидкостях и газе" - скачать бесплатно Сложное движение
Сложное движение Реактивное движение в природе Реактивное движение – это движение, возникающее при отделении от тела с некоторой скоростью какой-
Реактивное движение в природе Реактивное движение – это движение, возникающее при отделении от тела с некоторой скоростью какой- Перенесення і транспортування потерпілого
Перенесення і транспортування потерпілого  Внутрішнє тертя
Внутрішнє тертя Виконали : Рожко Вікторія Марченко Крістіна
Виконали : Рожко Вікторія Марченко Крістіна  Банк экспериментальных заданий для проведения ОГЭ по физике
Банк экспериментальных заданий для проведения ОГЭ по физике Общие сведения о передачах
Общие сведения о передачах Трёхфазные цепи
Трёхфазные цепи Сила Ампера. Движение заряженных частиц в магнитном поле. Задачи
Сила Ампера. Движение заряженных частиц в магнитном поле. Задачи Летательный аппарат ракета
Летательный аппарат ракета Капиллярлық құбылыстар
Капиллярлық құбылыстар Роль физики в жизни кошки
Роль физики в жизни кошки Неинерциальные системы отсчета
Неинерциальные системы отсчета Відкриття електромагнітних хвиль Презентація 11-А класу швеця максима і пивоварчука вадима
Відкриття електромагнітних хвиль Презентація 11-А класу швеця максима і пивоварчука вадима  Расчёт сооружений на действие подвижных и других временных нагрузок
Расчёт сооружений на действие подвижных и других временных нагрузок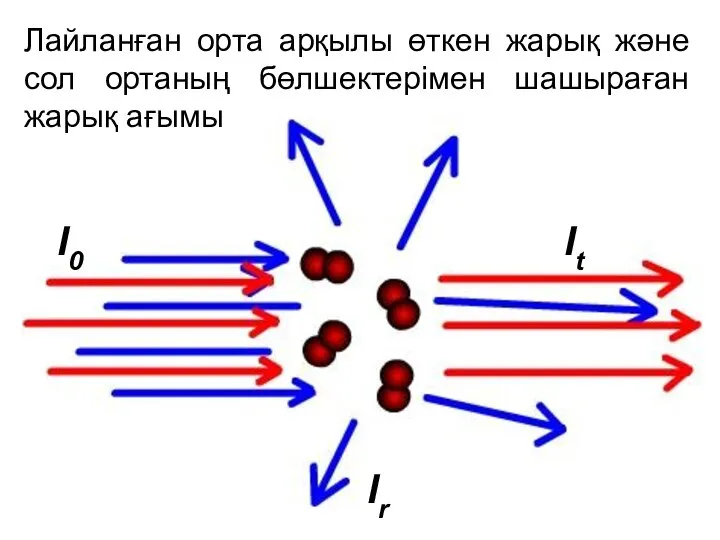 Лайланған орта арқылы өткен жарық және сол ортаның бөлшектерімен шашыраған жарық ағымы
Лайланған орта арқылы өткен жарық және сол ортаның бөлшектерімен шашыраған жарық ағымы Испарение. Конденсация. Кипение
Испарение. Конденсация. Кипение