Содержание
- 2. Статистические гипотезы Основные этапы проверки статистической гипотезы Этап 1. Формулируется проверяемая гипотеза (H0) и выдвигается альтернативную
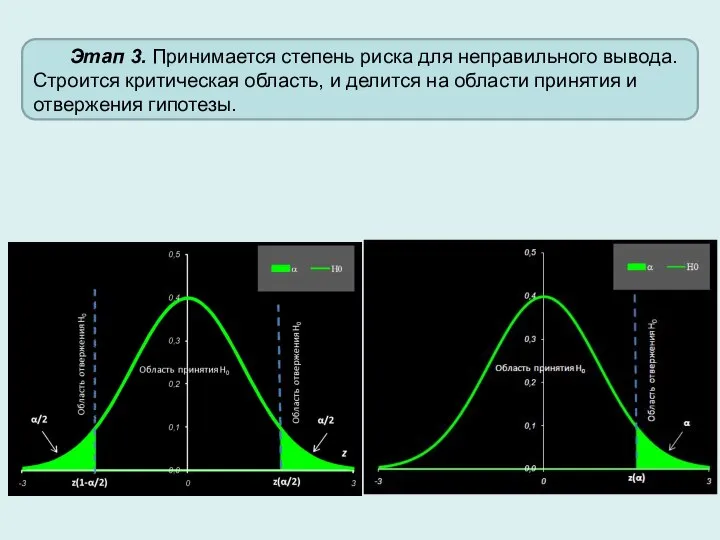
- 4. Этап 3. Принимается степень риска для неправильного вывода. Строится критическая область, и делится на области принятия
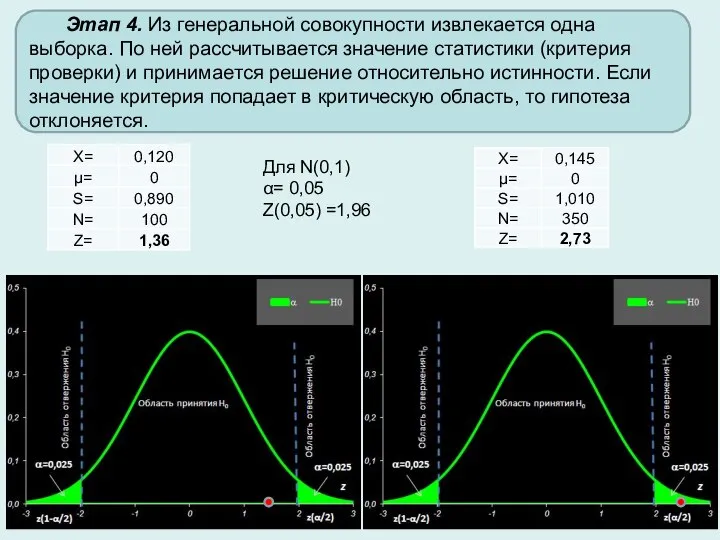
- 5. Этап 4. Из генеральной совокупности извлекается одна выборка. По ней рассчитывается значение статистики (критерия проверки) и
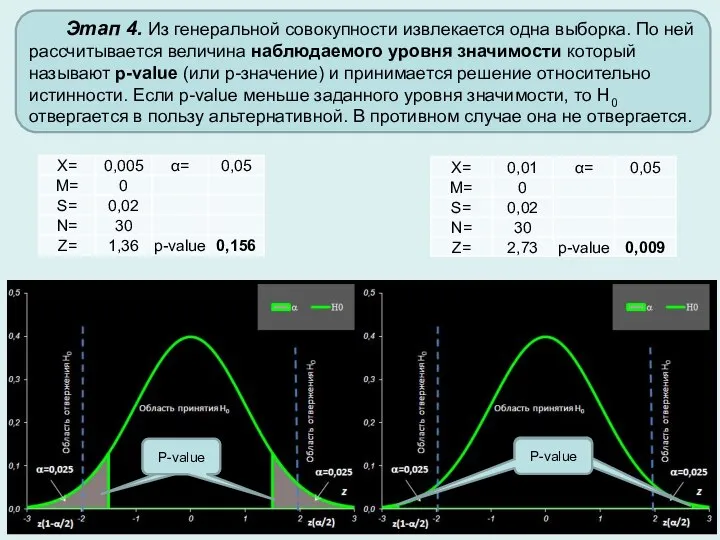
- 6. Этап 4. Из генеральной совокупности извлекается одна выборка. По ней рассчитывается величина наблюдаемого уровня значимости который
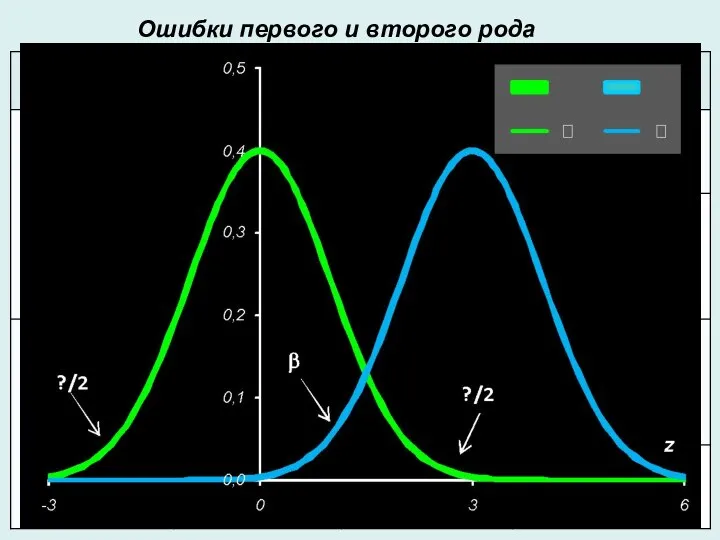
- 7. Ошибки первого и второго рода
- 8. Выбор уровня значимости При выборе гипотезы следует учитывать те потери, штрафы, которые несет исследователь и потребитель
- 9. Проверка нормальности распределения результатов измерения С помощью χ2-критерия (критерия Пирсона) Н0: Распределение соответствует нормальному распределению Ранжирование
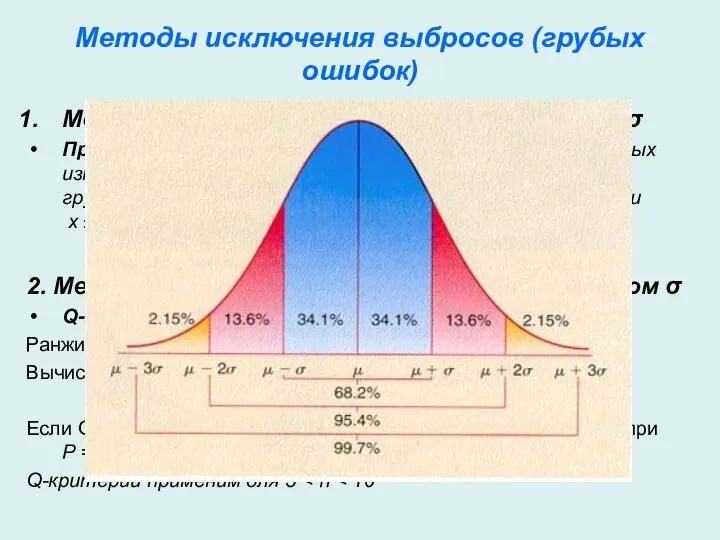
- 10. Методы исключения выбросов (грубых ошибок) Метод исключения выбросов при известном σ Правило «трех σ»: одно, по
- 11. r-критерий Н0: сомнительное значение х, принадлежит данной совокупности. Вычисляют и сопоставляют его с табличным значением rкрит
- 13. Сравнение двух дисперсий Имеем две серии измерений : x1, x2,...,xi...,xn1 и у1, у2,…..уj,…..уn2, выборочные дисперсии S12
- 14. 2-й случай. Сравнивают дисперсии S12 и S22, при справедливости любого из трех положений σ12 > σ22
- 15. Сравнение нескольких дисперсий Имеем несколько (m) дисперсий : S12, S22, S32,...,Sm2, каждая из которых определена с
- 16. Сравнение нескольких дисперсий
- 17. Сравнение двух средних результатов
- 20. Оценка доверительных интервалов выборочных характеристик 1. Оценка доверительного интервала среднего результата - пределы нахождения истинного значения
- 21. Оценка доверительных интервалов выборочных характеристик 2. Оценка доверительного интервала дисперсии и стандартного отклонения Доверительный интервал указывает,
- 22. Оценка доверительных интервалов выборочных характеристик 2. Оценка доверительного интервала дисперсии и стандартного отклонения Доверительный интервал для
- 24. Скачать презентацию
















 Аттестационная работа. Рабочая программа дополнительного образования. Кружок по физике: Удивительная физика 6 класс
Аттестационная работа. Рабочая программа дополнительного образования. Кружок по физике: Удивительная физика 6 класс Манометры. Поршневой жидкостный насос
Манометры. Поршневой жидкостный насос Измерение размеров малых объектов с помощью микроскопа
Измерение размеров малых объектов с помощью микроскопа Моделирование взаимодействия деформируемого ударника с металлической преградой в пакете LS-DYNA
Моделирование взаимодействия деформируемого ударника с металлической преградой в пакете LS-DYNA Механическая работа и энергия
Механическая работа и энергия Применение сообщающихся сосудов
Применение сообщающихся сосудов Презентация по физике Реальные газы, жидкости и вещества
Презентация по физике Реальные газы, жидкости и вещества  Упругие напряжения и обратимые деформации. (Лекция 10)
Упругие напряжения и обратимые деформации. (Лекция 10) Регуляторы для движения по границе черного и белого в TRIK Studio
Регуляторы для движения по границе черного и белого в TRIK Studio Физика на кухне
Физика на кухне Неионизирующие излучения электромагнитного диапазона
Неионизирующие излучения электромагнитного диапазона Центр тяжести
Центр тяжести Исследовательская работа по теме: «Фруктовые и овощные батарейки».
Исследовательская работа по теме: «Фруктовые и овощные батарейки». Постоянный электрический ток. Причины электрического тока
Постоянный электрический ток. Причины электрического тока Закон сохранения и превращения механической энергии
Закон сохранения и превращения механической энергии  Механика. Подготовка к ЕГЭ
Механика. Подготовка к ЕГЭ …Отдельно взятые черты Всецельно дышащей природы! Какая вас связала нить, Одна другой светлей и краше? Каким законом объяснить Родство таинственное наше? А.К.Толстой Оптические явления в природе
…Отдельно взятые черты Всецельно дышащей природы! Какая вас связала нить, Одна другой светлей и краше? Каким законом объяснить Родство таинственное наше? А.К.Толстой Оптические явления в природе Тема: Гелиоэнергетика: преобразование солнечной энергии в тепловую.
Тема: Гелиоэнергетика: преобразование солнечной энергии в тепловую. Презентация по физике "Законы сохранения в механике" - скачать бесплатно
Презентация по физике "Законы сохранения в механике" - скачать бесплатно Урок физики в 9 классе по теме: «Конденсатор» Разработала: Учитель физики
Урок физики в 9 классе по теме: «Конденсатор» Разработала: Учитель физики  Управление образования г. Снежинска МБОУ СОШ №117 ФИЗИКА ( 9 класс ) Третий закон Ньютона Дмитракова Лариса Николаевна, учитель фи
Управление образования г. Снежинска МБОУ СОШ №117 ФИЗИКА ( 9 класс ) Третий закон Ньютона Дмитракова Лариса Николаевна, учитель фи Моточные изделия: катушка индуктивности
Моточные изделия: катушка индуктивности Pārejas procesi maiņstrāvas piedziņā
Pārejas procesi maiņstrāvas piedziņā Презентация по физике "История создания тепловых двигателей" - скачать
Презентация по физике "История создания тепловых двигателей" - скачать  Диагностика системы электроснабжения
Диагностика системы электроснабжения Закат как физическое явление
Закат как физическое явление Контрольная работа 1 по теме Кинематика
Контрольная работа 1 по теме Кинематика Презентация по физике "Радуга-дуга, ведёшь куда?" - скачать
Презентация по физике "Радуга-дуга, ведёшь куда?" - скачать