Содержание
- 2. Цель: Познакомить учащихся с жизнью Пифагора и его теоремой
- 3. Задачи: 1. Формировать у учащихся умения и навыки самостоятельной работы; 2. Развивать их мышление; 3. Готовить
- 5. Пифагорейская школа
- 6. Пифагорейская звезда Пифагорейские треугольники Гордость пифагорейской мысли Пифагор и музыка Пифагор и теория чисел Золотое сечение
- 7. Задание классу: Из нарисованного правильного пятиугольника построить звезду
- 10. Доказать, что сумма углов пентаграмма равна 180º
- 11. Доказательство: Сумма углов правильного пятиугольника равна 180º·(5-2)=540º. Каждый угол равен 540º:5 = 108º. Смежный с ним
- 12. Пифагорейские треугольники Некоторые пифагоровы тройки : (3, 4, 5), (6, 8, 10), (5, 12, 13), (9,
- 13. Задание классу: Построить треугольник со сторонами 3,4,5 и на его сторонах построить квадраты и сделать вывод.
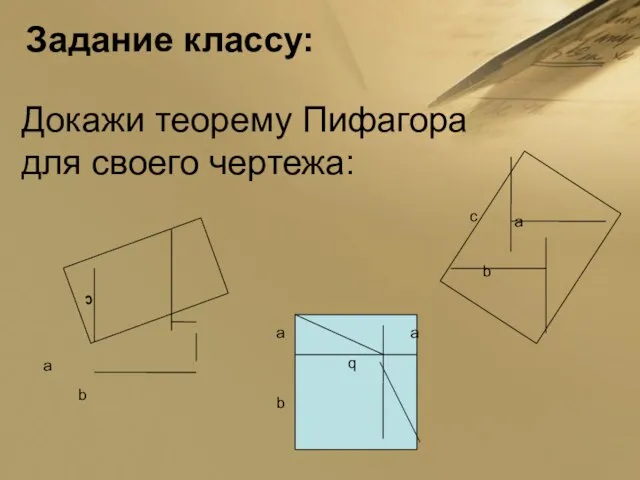
- 14. Вывод: Квадрат, построенный на гипотенузе, имеет площадь, равную сумме площадей квадратов, построенных на катетах
- 15. Гордость Пифагорейской мысли
- 16. Задание классу: Заполнить таблицу:
- 17. Задание классу: Докажи теорему Пифагора для своего чертежа:
- 18. Пифагор и музыка
- 19. Пифагор и теория чисел 2m-четное число 2n+1 – нечетное число (2m+1)+(2n+1) = 2(m+n+1) 2m+(2n+1)= 2(m+n)+1 2m
- 20. Золотое сечение Что такое ЗОЛОТОЕ СЕЧЕНИЕ? Гармония пропорций в природе, математике и искусстве. Иоганн Kеплер говорил,
- 21. Золотое сечение - гармоническая пропорция В математике пропорцией (лат. proportio) называют равенство двух отношений: a :
- 22. В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми пользовались архитекторы
- 23. Золотые пропорции в частях тела человека
- 24. Золотые пропорции в фигуре человека
- 26. Скачать презентацию






















 Центральная симметрия.
Центральная симметрия. Тетраэдр - презентация по Геометрии
Тетраэдр - презентация по Геометрии Прямоугольный треугольник - презентация по Геометрии
Прямоугольный треугольник - презентация по Геометрии Презентация по геометрии Сравнение и измерение отрезков
Презентация по геометрии Сравнение и измерение отрезков  Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников  Геометрия и лист бумаги Работа учащихся 7 класса МОУ сш № 78
Геометрия и лист бумаги Работа учащихся 7 класса МОУ сш № 78  Измерение углов 5 класс - презентация_
Измерение углов 5 класс - презентация_ Перпендикуляр и наклонные
Перпендикуляр и наклонные Работа выполнена в рамках проекта «Повышение квалификации различных категорий работников образования и формирования у них базов
Работа выполнена в рамках проекта «Повышение квалификации различных категорий работников образования и формирования у них базов Построение сечений тетраэдра
Построение сечений тетраэдра Тема урока: Построение сечений параллелепипеда
Тема урока: Построение сечений параллелепипеда  ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР НА ПЛОСКОСТИ
ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР НА ПЛОСКОСТИ  Что изучает геометрия - презентация по Геометрии
Что изучает геометрия - презентация по Геометрии Второй признак равенства треугольников Цели урока: 1)доказать второй признак равенства треугольников, 1)выработать у учащихся на
Второй признак равенства треугольников Цели урока: 1)доказать второй признак равенства треугольников, 1)выработать у учащихся на Объём. Цилиндр, призма - презентация по Геометрии_
Объём. Цилиндр, призма - презентация по Геометрии_ Задачи на построение сечений куба - презентация по Геометрии
Задачи на построение сечений куба - презентация по Геометрии Поворот - презентация по Геометрии
Поворот - презентация по Геометрии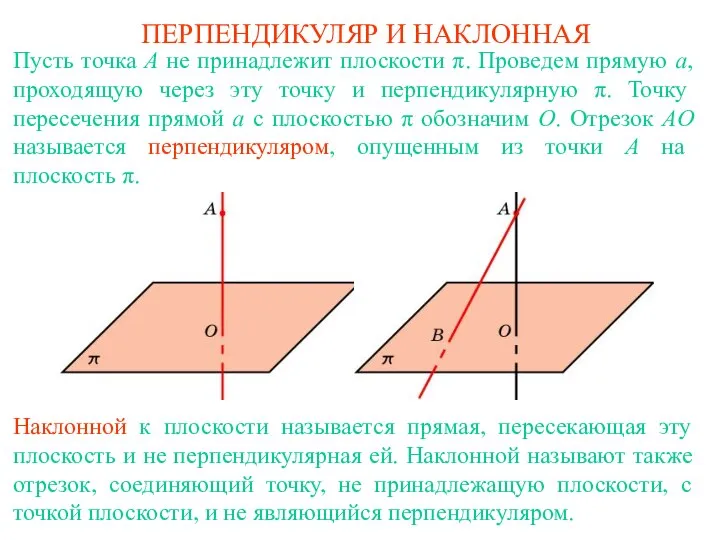 ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ
ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ НЕБЕСНАЯ ГЕОМЕТРИЯ
НЕБЕСНАЯ ГЕОМЕТРИЯ  Тема урока «Прямоугольник. Ромб. Квадрат.»
Тема урока «Прямоугольник. Ромб. Квадрат.»  Длина окружности и площадь круга. Решение задач.
Длина окружности и площадь круга. Решение задач.  Круг и окружность - презентация по Геометрии_
Круг и окружность - презентация по Геометрии_ «Симметрия относительно прямой» и «Класс насекомых»
«Симметрия относительно прямой» и «Класс насекомых»  Геометрия 8 класс Свойства параллелограмма (приложения к уроку) Сокирко Светлана Петровна учитель математики и физики МОУ «СОШ
Геометрия 8 класс Свойства параллелограмма (приложения к уроку) Сокирко Светлана Петровна учитель математики и физики МОУ «СОШ Презентация по геометрии Центральные углы и углы, вписанные в окружность
Презентация по геометрии Центральные углы и углы, вписанные в окружность УРОК геометрии 5 класс. «Виды треугольников. Построение».
УРОК геометрии 5 класс. «Виды треугольников. Построение». Звездный час многогранников МКОУ «Унъюганская СОШ №2» учитель математики Ярикова Т.В.
Звездный час многогранников МКОУ «Унъюганская СОШ №2» учитель математики Ярикова Т.В. Геометрия - презентация по Геометрии_
Геометрия - презентация по Геометрии_