Содержание
- 2. Аполлоний Пергский (Ἀπολλώνιος ὁ Περγαῖος, Перге, 262 до н. э. — 190 до н. э.) —
- 3. Подумаем, как можно получить массу информации о коэффициентах квадратного трехчлена у =ах2 + bх + с,
- 4. 2) Коэффициент b (вместе с а) определяет абсциссу вершины параболы: В частности, при а = 1
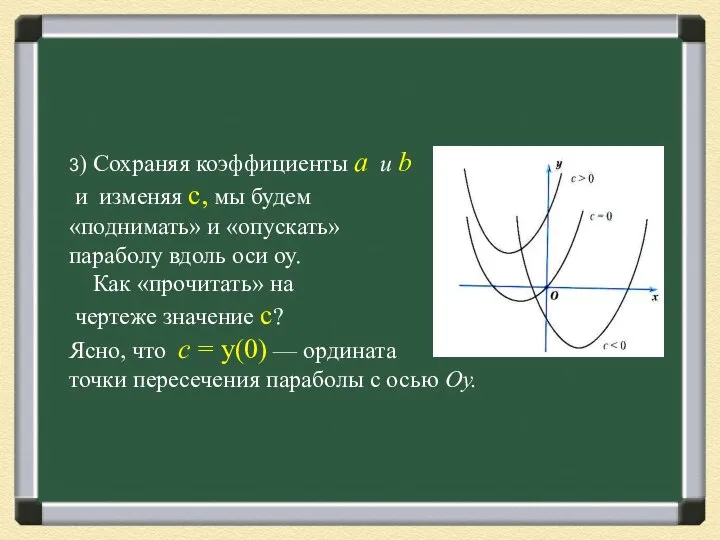
- 5. 3) Сохраняя коэффициенты a и b и изменяя с, мы будем «поднимать» и «опускать» параболу вдоль
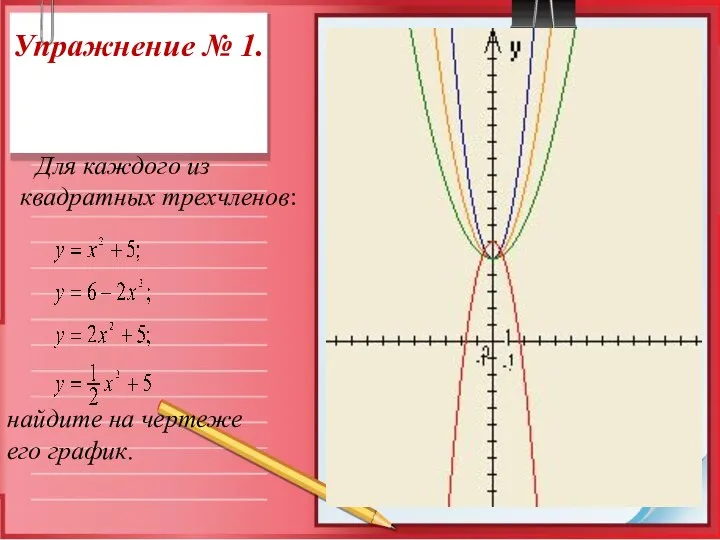
- 6. Упражнение № 1. Для каждого из квадратных трехчленов: найдите на чертеже его график.
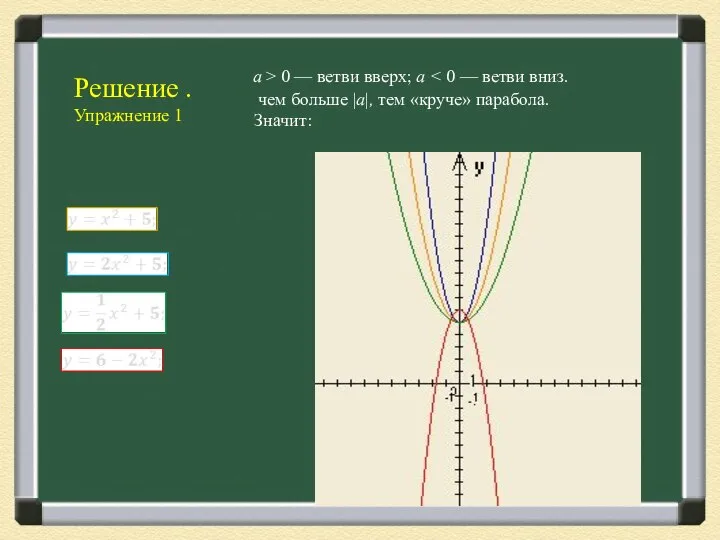
- 7. а > 0 — ветви вверх; а чем больше |a|, тем «круче» парабола. Значит: Решение .
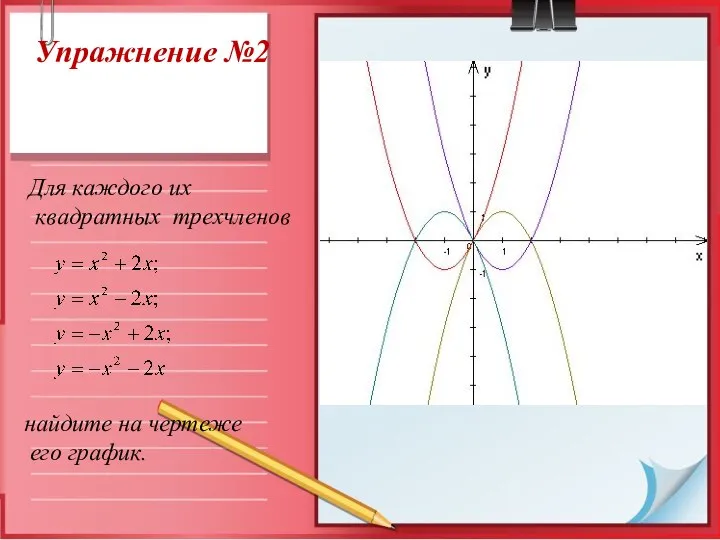
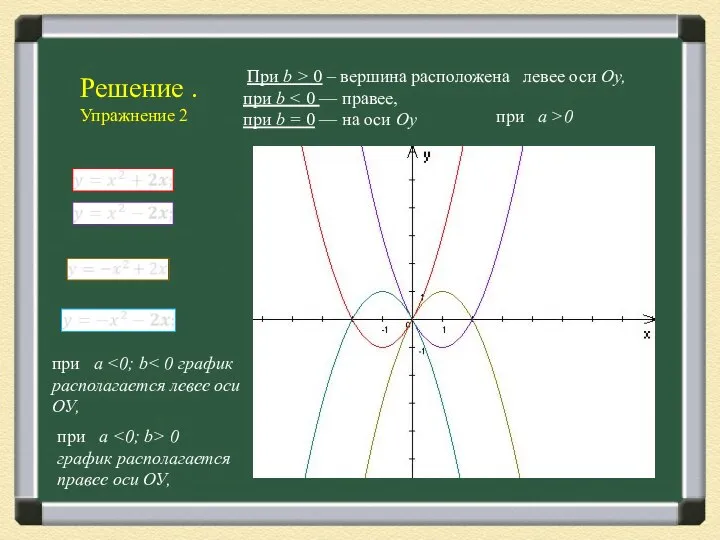
- 8. Упражнение №2 Для каждого их квадратных трехчленов найдите на чертеже его график.
- 9. Решение . Упражнение 2 При b > 0 – вершина расположена левее оси Оу, при b
- 10. А теперь, когда мы вспомнили как влияют коэффициенты на построение графика параболы выполним следующие упражнения:
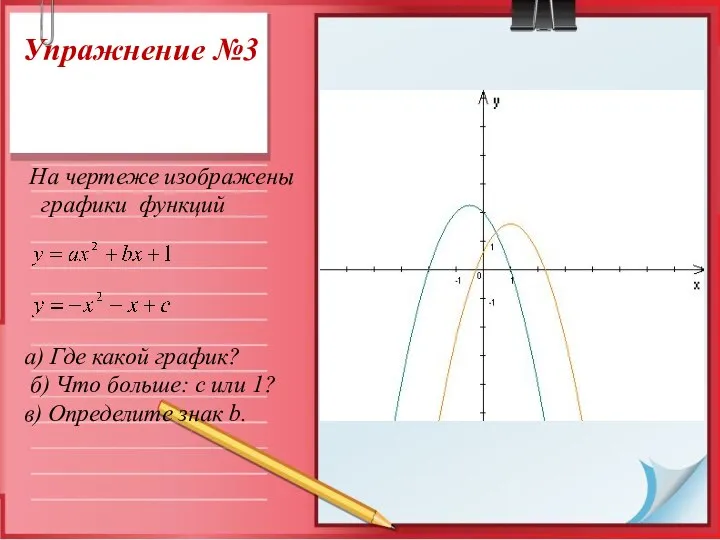
- 11. Упражнение №3 На чертеже изображены графики функций а) Где какой график? б) Что больше: с или
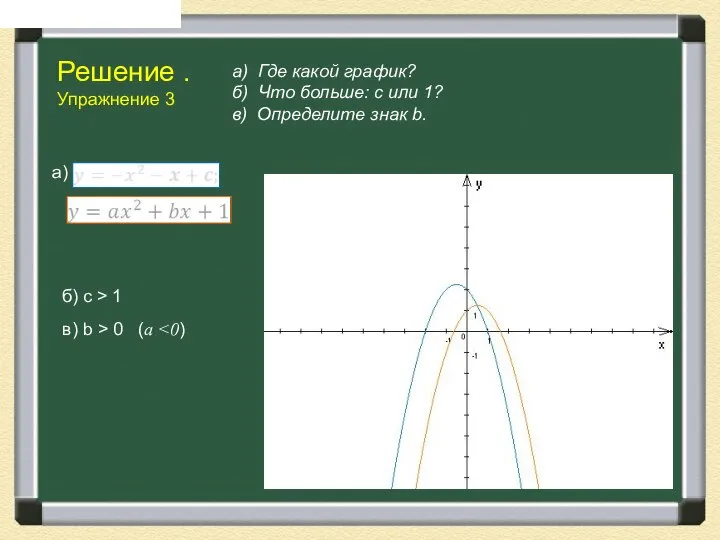
- 12. Решение . Упражнение 3 а) Где какой график? б) Что больше: с или 1? в) Определите
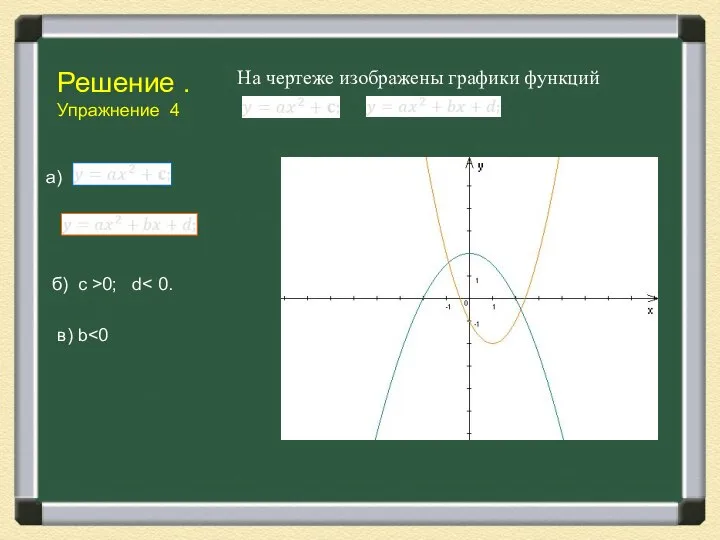
- 13. Упражнение №4 На чертеже изображены графики функций причем ось оу , идущая, как всегда, «снизу вверх»
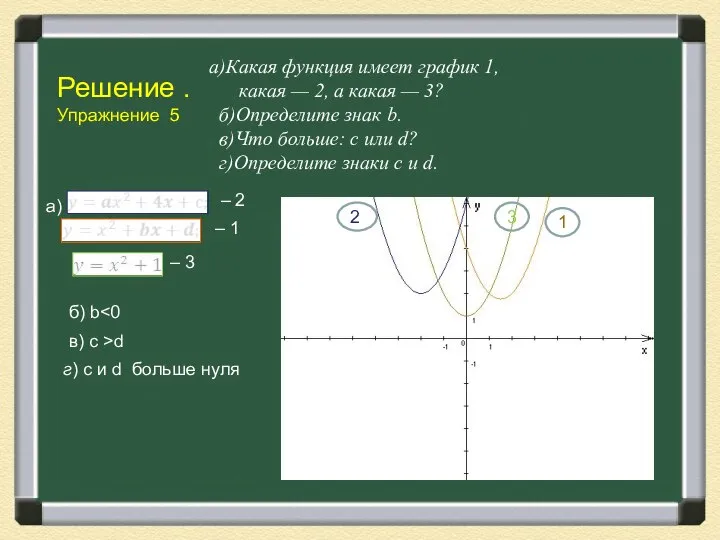
- 14. Решение . Упражнение 4 На чертеже изображены графики функций а) б) c >0; d в) b
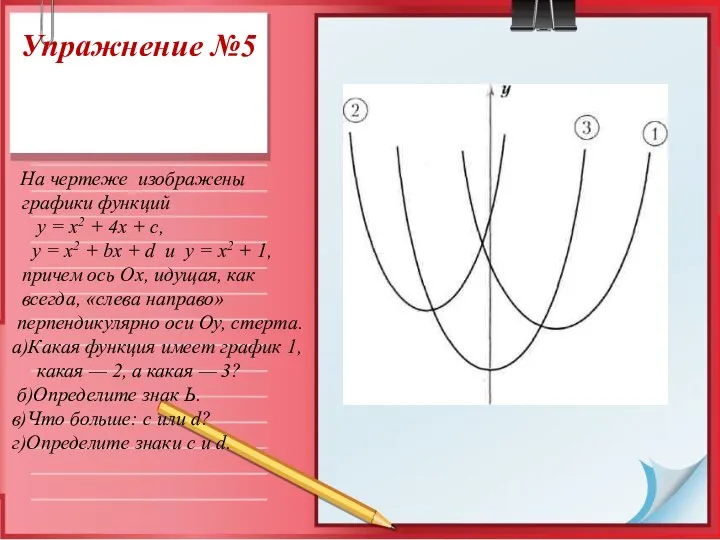
- 15. Упражнение №5 На чертеже изображены графики функций у = х2 + 4х + с, у =
- 16. Решение . Упражнение 5 а)Какая функция имеет график 1, какая — 2, а какая — 3?
- 17. Упражнение №6. На чертеже изображены графики функций у = ах2 + х + с и у
- 18. Решение . Упражнение 6 а) Определите знак b б) Определите знак с. в) Докажите, что у
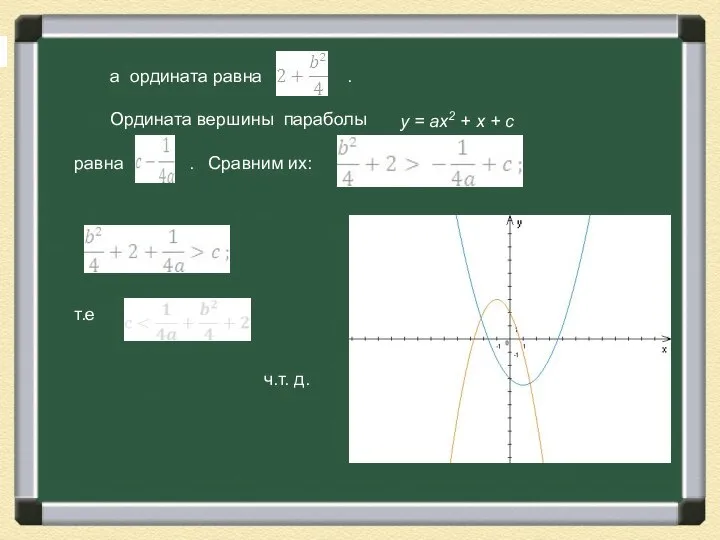
- 19. а ордината равна . Ордината вершины параболы равна . Сравним их: т.е ч.т. д. у =
- 20. Решение упражнений основывается на тех фактах, которые мы знаем о коэффициентах квадратного трехчлена. Свойства параболы чрезвычайно
- 21. Задача. Известно, что парабола, являющаяся графиком квадратного трехчлена у = ах2 + 10х + с, не
- 22. Решение. Поскольку парабола не имеет точек в III четверти, то не может быть отрицательным. Итак, ,следовательно,
- 23. Самые близкие родственники параболы – это окружность, гипербола и эллипс. У этого термина существуют и другие
- 25. Скачать презентацию











 Цилиндр, конус, шар.
Цилиндр, конус, шар. Геометрические формы - презентация по Геометрии
Геометрические формы - презентация по Геометрии ВОЗНИКНОВЕНИЕ ГЕОМЕТРИИ учитель: Ксензюк Л.П. ГЕОМЕТРИЯ – ЭТО НАУКА ХОРОШО ИЗМЕРЯТЬ. П. РАМУС
ВОЗНИКНОВЕНИЕ ГЕОМЕТРИИ учитель: Ксензюк Л.П. ГЕОМЕТРИЯ – ЭТО НАУКА ХОРОШО ИЗМЕРЯТЬ. П. РАМУС  Подобные треугольники. Выполнили: Карташов Алексей Пучков Евгений
Подобные треугольники. Выполнили: Карташов Алексей Пучков Евгений Введение в геометрию класс - презентация по Геометрии_
Введение в геометрию класс - презентация по Геометрии_ МОУ СОШ № 256 г.Фокино Приморского края. Каратанова Марина Николаевна.
МОУ СОШ № 256 г.Фокино Приморского края. Каратанова Марина Николаевна.  Чертежи разъемных и неразъемных соединений деталей Выполнила ученица 9 в кл. МОУ лицея №1 Осипянц Милена Учитель черчения Плот
Чертежи разъемных и неразъемных соединений деталей Выполнила ученица 9 в кл. МОУ лицея №1 Осипянц Милена Учитель черчения Плот ПРАКТИЧЕСКАЯ ГЕОМЕТРИЯ У РАЗНЫХ НАРОДОВ МИРА
ПРАКТИЧЕСКАЯ ГЕОМЕТРИЯ У РАЗНЫХ НАРОДОВ МИРА История теоремы Пифагора - презентация по Геометрии
История теоремы Пифагора - презентация по Геометрии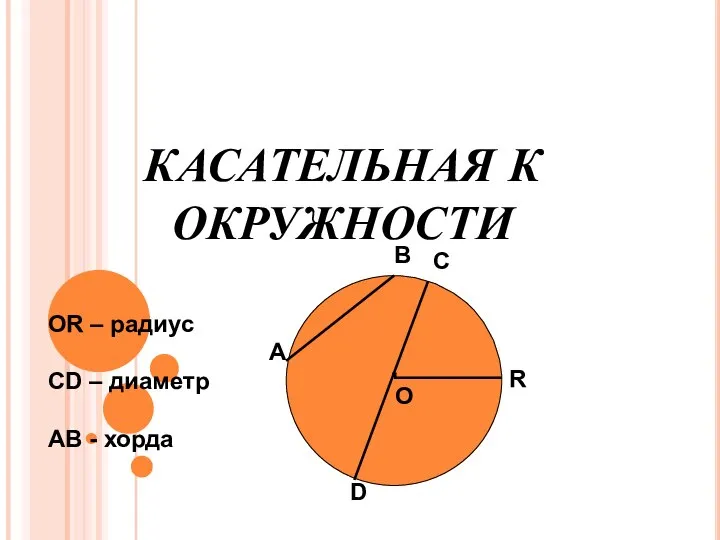 КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ
КАСАТЕЛЬНАЯ К ОКРУЖНОСТИ  Тригонометрические функции любого угла. Определение синуса, косинуса, тангенса и котангенса.
Тригонометрические функции любого угла. Определение синуса, косинуса, тангенса и котангенса. Презентация по геометрии ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Презентация по геометрии ПРАВИЛЬНЫЕ МНОГОГРАННИКИ  Теорема о трех перпендикулярах
Теорема о трех перпендикулярах  Вписанные и описанные многоугольники - презентация по Геометрии
Вписанные и описанные многоугольники - презентация по Геометрии Прямоугольный труегольник - презентация по Геометрии
Прямоугольный труегольник - презентация по Геометрии Прямоугольная система координат в пространстве. Геометрия – 11 класс
Прямоугольная система координат в пространстве. Геометрия – 11 класс Параллелепипед - презентация по Геометрии__
Параллелепипед - презентация по Геометрии__ Геометрия Лобачевского - презентация по Геометрии
Геометрия Лобачевского - презентация по Геометрии ГЕОМЕТРИЯ 8 КЛАСС
ГЕОМЕТРИЯ 8 КЛАСС  ТЕМА ПРОЕКТА: «Фундамент геометрии из четырех углов» для учащихся 8кл.
ТЕМА ПРОЕКТА: «Фундамент геометрии из четырех углов» для учащихся 8кл.  Многогранники
Многогранники  Урок математики «Геометрия площади» 6 класс Предисловие учителя Урок математики «Геометрия площади
Урок математики «Геометрия площади» 6 класс Предисловие учителя Урок математики «Геометрия площади Тригонометрические функции числового аргумента - презентация по Геометрии
Тригонометрические функции числового аргумента - презентация по Геометрии Круги Эйлера и их практическое применение - презентация по Геометрии_
Круги Эйлера и их практическое применение - презентация по Геометрии_ Решение задач по теме «прямые на плоскости и в пространстве» Учитель математики Кировской МБОУ Ткачук Н. П.
Решение задач по теме «прямые на плоскости и в пространстве» Учитель математики Кировской МБОУ Ткачук Н. П. Многогранники: виды задач и методы их решения (типовые задания С2) - 2 - презентация по Геометрии_
Многогранники: виды задач и методы их решения (типовые задания С2) - 2 - презентация по Геометрии_ Конкурс «Будущее уже наступило» Номинация «Я иду на урок» Косова Ольга Михайловна, учитель черчения МОУ «СОШ№1»
Конкурс «Будущее уже наступило» Номинация «Я иду на урок» Косова Ольга Михайловна, учитель черчения МОУ «СОШ№1»