Примем точку О за начало прямоугольной системы координат, оси Ох
придадим направление вектора OD и будем считать единицей масштаба.
В данной системе точки A, D, B имеют координаты:
А (-2;0), D (2;0) и В (0;b).
Способ первый:
Координатный
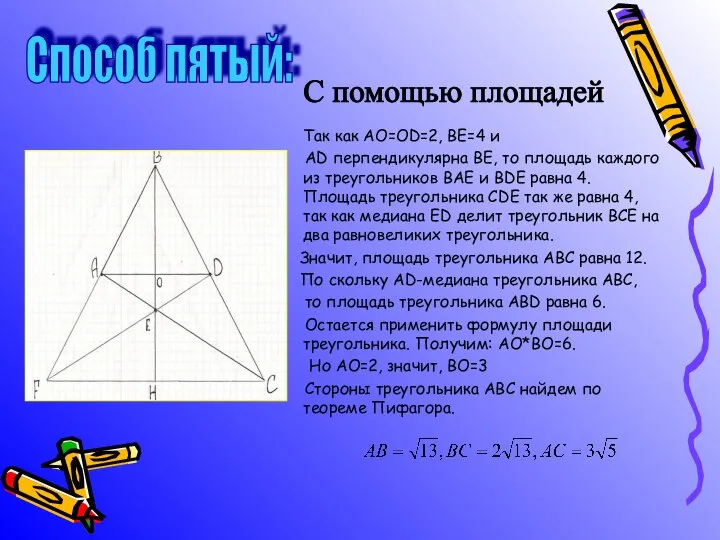
Для того чтобы определить длины сторон треугольника АВС, надо найти число b. Выразим через b координаты точек С и Е. Так как D – середина отрезка ВС, то С (4;-b). Для точки Е имеем координаты (0;у). Вторую координату точки Е найдем, пользуясь, тем что точка Е принадлежит прямой АС. Уравнение прямой АС имеет вид:
Координаты точки Е (0;у) удовлетворяют этому уравнению. Подставив в него 0 вместо х, получим: Следовательно, По условию задачи ВЕ=4, значит, , или b=3.
Итак, А (-2;0), В (0;3), С (4;-3). Зная координаты вершин треугольника АВС, найдем его стороны:













 Графы и их применение (подготовка к ЕГЭ) Мастер – класс учитель Майсова Т.Б.
Графы и их применение (подготовка к ЕГЭ) Мастер – класс учитель Майсова Т.Б. Вероятность и геометрия
Вероятность и геометрия  Четырехугольники вокруг нас Выполнила команда «Звёздочки» МКУО Тумановская СОШ Руководитель команды: Бирих Татьяна Викторовна
Четырехугольники вокруг нас Выполнила команда «Звёздочки» МКУО Тумановская СОШ Руководитель команды: Бирих Татьяна Викторовна Соединения деталей - презентация по Геометрии_
Соединения деталей - презентация по Геометрии_ СТАРОЕ И НОВОЕ О КРУГЕ Ученица 10 А класса БуРганова Алсу Учитель математики Зайнуллина Г.З.
СТАРОЕ И НОВОЕ О КРУГЕ Ученица 10 А класса БуРганова Алсу Учитель математики Зайнуллина Г.З. Тела вращения
Тела вращения ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Наглядное пособие для уроков черчения Учитель: Бурякова И.М.
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ Наглядное пособие для уроков черчения Учитель: Бурякова И.М.  Сечения тетраэдра - презентация по Геометрии_
Сечения тетраэдра - презентация по Геометрии_ Презентация по геометрии Двугранный угол
Презентация по геометрии Двугранный угол Презентация по геометрии На тему: Системы координат
Презентация по геометрии На тему: Системы координат 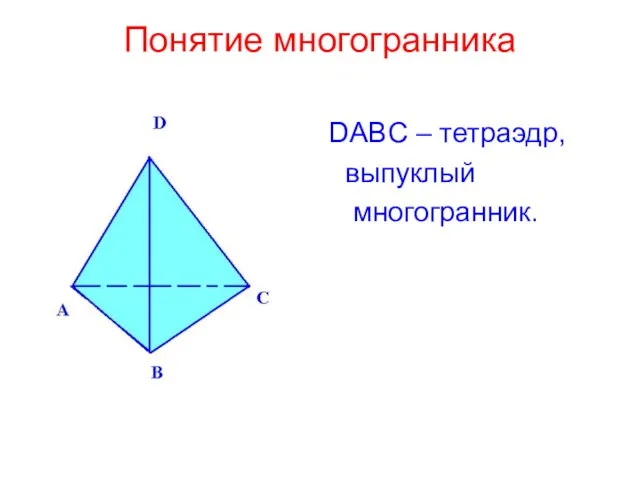 Понятие многогранника DABC – тетраэдр, выпуклый многогранник.
Понятие многогранника DABC – тетраэдр, выпуклый многогранник. ПИФАГОР И ЕГО ТЕОРЕМА ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА УЧЕНИКА 8 КЛАСС БРУСОВСКОЙ СОШ УД
ПИФАГОР И ЕГО ТЕОРЕМА ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА УЧЕНИКА 8 КЛАСС БРУСОВСКОЙ СОШ УД Векторы в пространстве
Векторы в пространстве  Сфера - презентация по Геометрии
Сфера - презентация по Геометрии Треугольник Устные задачи - презентация по Геометрии_
Треугольник Устные задачи - презентация по Геометрии_ Параллельные прямые - презентация (7 класс)
Параллельные прямые - презентация (7 класс) Решение задач по теме Цилиндр - презентация по Геометрии
Решение задач по теме Цилиндр - презентация по Геометрии Геометрия и лист бумаги Работа учащихся 7 класса МОУ сш № 78
Геометрия и лист бумаги Работа учащихся 7 класса МОУ сш № 78 Решение задач по теме «ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК». МОУ СОШ № 256 г. Фокино 9 класс.
Решение задач по теме «ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК». МОУ СОШ № 256 г. Фокино 9 класс.  Пирамиды Подготовили ученицы 5 класса «А» Власова Анастасия и Шустикова Анастасия
Пирамиды Подготовили ученицы 5 класса «А» Власова Анастасия и Шустикова Анастасия Равнобедренный треугольник и его свойства - презентация по Геометрии
Равнобедренный треугольник и его свойства - презентация по Геометрии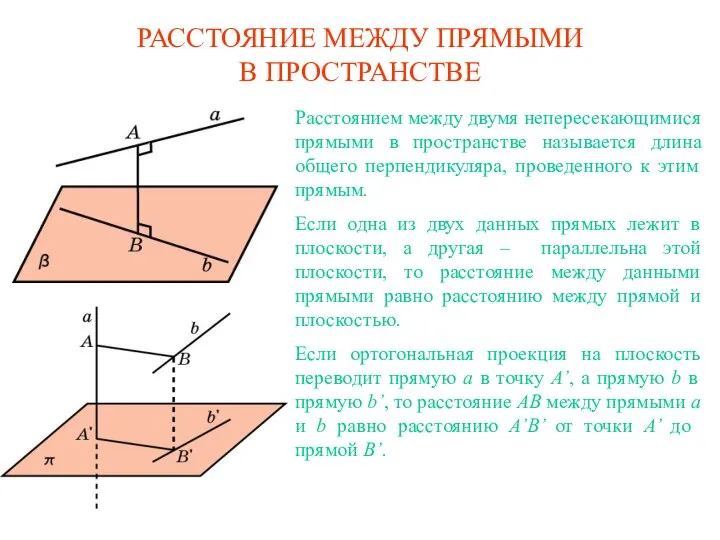 РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Элективный курс «Геометрия вокруг нас» Выполнила Яковлева Л.В.
Элективный курс «Геометрия вокруг нас» Выполнила Яковлева Л.В.  Поворот и центральная симметрия Михарева Галина Валентиновна учитель математики МБОУ СОШ №3 г. Пущино Московской области
Поворот и центральная симметрия Михарева Галина Валентиновна учитель математики МБОУ СОШ №3 г. Пущино Московской области Медиана, биссектриса и высота треугольника - презентация по Геометрии
Медиана, биссектриса и высота треугольника - презентация по Геометрии Геометрические преобразования и паркеты
Геометрические преобразования и паркеты Введение
Введение Удивительные фигуры - презентация по Геометрии_
Удивительные фигуры - презентация по Геометрии_