Содержание
- 2. Это учебник создан для экзамена по геометрии. В нем рассмотрена темы 10-го класса- Векторы в пространстве,
- 3. Абсолютная величина и направление вектора. Векторы в пространстве Действия над векторами: Тест Об авторе Содержание
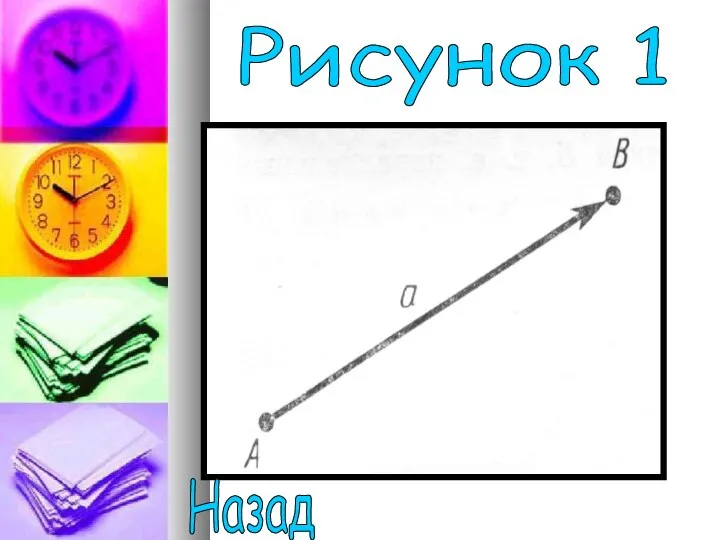
- 4. Вектором мы будем называть направленный отрезок (рисунок 1) . Направление вектора определяется указанием его начала и
- 5. Рисунок 1 Назад
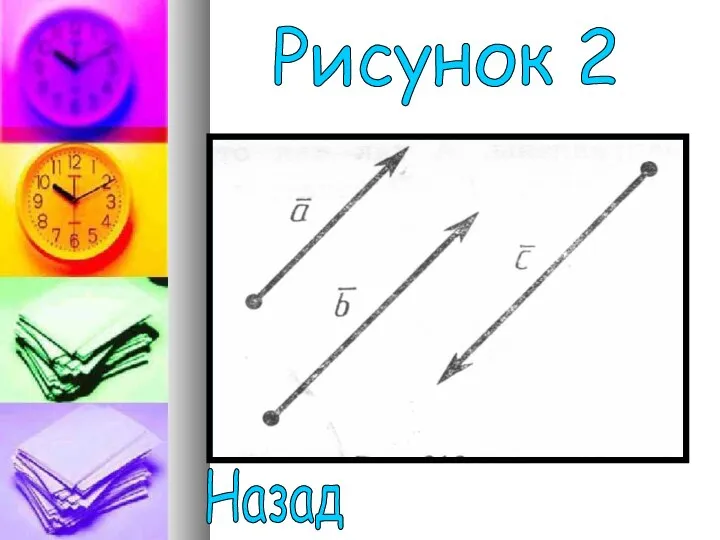
- 6. Векторы называются одинаково направленными, если полупрямые АВ и СD одинаково направлены. Векторы называются противоположно направленными, если
- 7. Рисунок 2 Назад
- 8. В пространстве, как и на плоскости, вектором называется направленный отрезок. Буквально так же, как и на
- 9. Так же, как и на плоскости, определяются действия над векторами: сложение, разность , умножение на число
- 10. Суммой векторов (a1; а2; а3) и (b1; b2; b3) называется вектор: (a1 + b1; а2 +
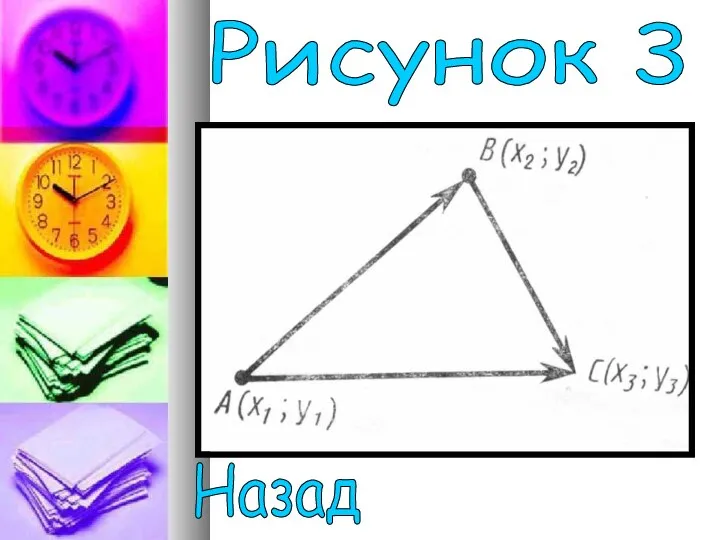
- 11. Пусть A (х1; у1),В(х2; у2),С(х3; у3) -данные точки (рисунок 3) .Вектор имеет координаты х2-х1,y2-y1, вектор имеет
- 12. Рисунок 3 Назад
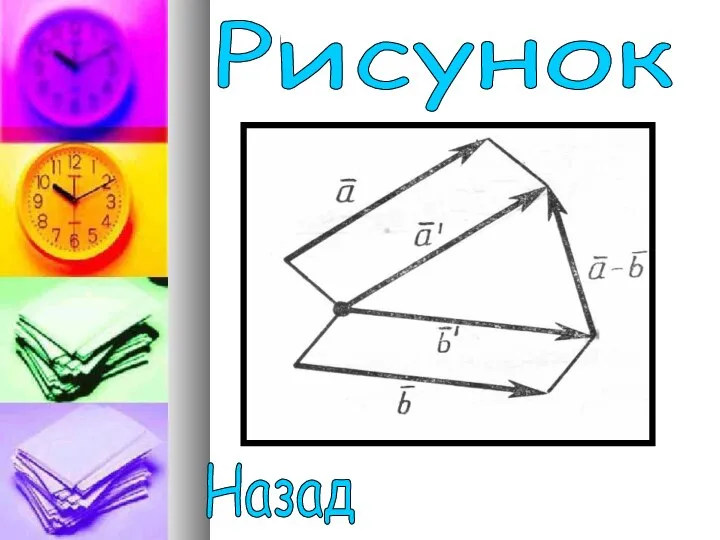
- 13. Разностью векторов (а1;а2;a3) и (b1; b2;b3) называется такой вектор (с1; с2;c3), который в сумме с вектором
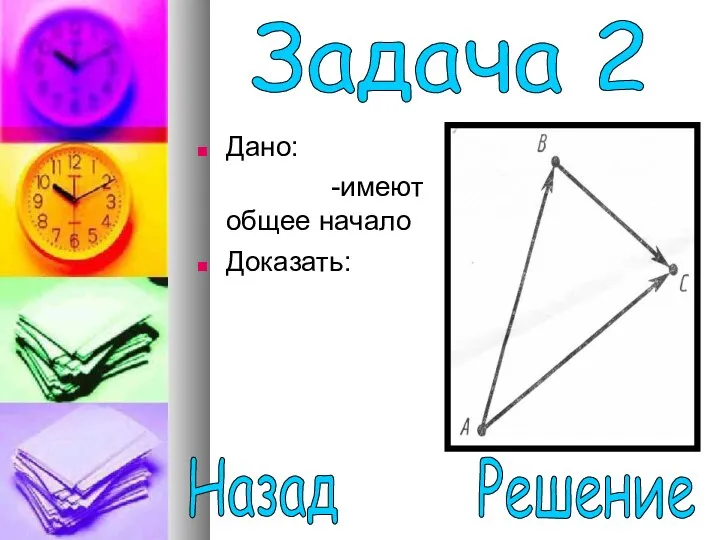
- 14. Дано: -имеют общее начало Доказать: Задача 2 Решение Назад
- 15. Решение: Задача 2 Назад Рисунок
- 16. Рисунок Назад
- 17. Дано: A(2;7;-3) B(1;0;3) C(-3;-4;5) D(-2;3;-1) Найти: Среди всех векторов указать равные Надо найти координаты всех векторов
- 18. Дано: (1;2;3) Найти: Коллинеарный вектор с началом в точке A(1;1;1) и концом B на плоскости xy.
- 19. Произведением вектора а(a1; а2; a3) на число λ называется вектор Так же, как и на плоскости,
- 20. Скалярным произведением векторов и называется число a1b1 +a2b2 +a3b3. Буквально так же, как и на плоскости,
- 21. Дано: A(0;1;-1) B(1;-1;2) C(3;1;0) D(2;-3;1) Найти: cosφ=? Решение: Координатами вектора будут: 1-0=1, -1-1=-2, 2-(-1)=3 Координатами вектора
- 23. Скачать презентацию















 Длина отрезка единицы измерения отрезков Урок геометрии в 7 классе
Длина отрезка единицы измерения отрезков Урок геометрии в 7 классе Презентация по геометрии Решение задачи по заданному условию, на тему: Параллельность прямых и плоскостей.
Презентация по геометрии Решение задачи по заданному условию, на тему: Параллельность прямых и плоскостей. Геометрия пирамида - презентация по Геометрии
Геометрия пирамида - презентация по Геометрии Правильные многоугольники и их виды - презентация по Геометрии
Правильные многоугольники и их виды - презентация по Геометрии Решение задач на тему «Прямоугольник. Ромб. Квадрат». Цель урока: Закрепить теоретический материал по теме «Прямоугольник. Ром
Решение задач на тему «Прямоугольник. Ромб. Квадрат». Цель урока: Закрепить теоретический материал по теме «Прямоугольник. Ром Параллельность в пространстве
Параллельность в пространстве Геометрия крестово-купольного храма Дружинина Вероника, класс 10а, гимназия №104 Руководитель: Борисова Е.А.
Геометрия крестово-купольного храма Дружинина Вероника, класс 10а, гимназия №104 Руководитель: Борисова Е.А. Тетраэдр
Тетраэдр Площадь круга Кузьмина Е.Ю. Гимназия №446 2005г.
Площадь круга Кузьмина Е.Ю. Гимназия №446 2005г. Исследовательский проект «Многогранники и кристаллы»
Исследовательский проект «Многогранники и кристаллы» основы геометрии
основы геометрии Прямоугольный параллелепипед - презентация по Геометрии_
Прямоугольный параллелепипед - презентация по Геометрии_ Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии
Проецирование предметов на две и три взаимно перпендикулярные плоскости проекций - презентация по Геометрии «Симметрия относительно прямой» и «Класс насекомых»
«Симметрия относительно прямой» и «Класс насекомых»  Урок – презентация. Составители: Каплунова Зоя Николаевна Шахавалова Татьяна Георгиевна МОУ «СОШ № 37» г. Кемерово
Урок – презентация. Составители: Каплунова Зоя Николаевна Шахавалова Татьяна Георгиевна МОУ «СОШ № 37» г. Кемерово Обобщение и систематизация сведений о треугольниках - презентация по Геометрии
Обобщение и систематизация сведений о треугольниках - презентация по Геометрии Урок 1. Прямая и отрезок. Геометрия (греческий, гео – земля, метрео – мерять, землемерие) – наука, занимающаяся изучением геометрич
Урок 1. Прямая и отрезок. Геометрия (греческий, гео – земля, метрео – мерять, землемерие) – наука, занимающаяся изучением геометрич Длина окружности - презентация по Геометрии
Длина окружности - презентация по Геометрии Урок «Четырехугольники» геометрия 8 класс Автор: учитель математики Комлякова Ксения Геннадьевна ГБОУ Гимназия №105, г. Сан
Урок «Четырехугольники» геометрия 8 класс Автор: учитель математики Комлякова Ксения Геннадьевна ГБОУ Гимназия №105, г. Сан Касательная к окружности - презентация по Геометрии
Касательная к окружности - презентация по Геометрии Начальные геометрические сведения
Начальные геометрические сведения Площадь круга и кругового сектора. Решение задач.
Площадь круга и кругового сектора. Решение задач. Вывод формулы Герона геометрия 8 класс
Вывод формулы Герона геометрия 8 класс ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Урок геометрии в 10 классе
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Урок геометрии в 10 классе  Две плоскости, cодержащие прямую DE - презентация по Геометрии_
Две плоскости, cодержащие прямую DE - презентация по Геометрии_ Моделирование многогранников. Архимедовы тела - презентация по Геометрии
Моделирование многогранников. Архимедовы тела - презентация по Геометрии Презентация Задачи на нахождение площади и периметра
Презентация Задачи на нахождение площади и периметра Тема: «Сумма углов треугольника» Геометрия 7 класс
Тема: «Сумма углов треугольника» Геометрия 7 класс