Алгоритмы поиска в строке

Июль 26, 2022

Главная
Информатика
Алгоритмы поиска в строке

Содержание

2. Поиск подстроки в строке — типичная задача поиска информации. На сегодняшний день существует огромное разнообразие алгоритмов
3. ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?
4. ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?
5. ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?
6. ЛИНЕЙНЫЙ ПОИСК Линейный, последовательный поиск (поиск методом полного перебора или брутфорса) — алгоритм нахождения заданного значения
7. ЛИНЕЙНЫЙ ПОИСК В связи с малой эффективностью по сравнению с другими алгоритмами линейный поиск обычно используют,
8. ЛИНЕЙНЫЙ ПОИСК Условие: дано два массива A и B. Нужно определить, является ли массив A подстрокой
9. АЛГОРИТМ БОЙЕРА-МУРА Алгоритм поиска строки Бойера-Мура, считается наиболее быстрым среди алгоритмов общего назначения, предназначенных для поиска
10. АЛГОРИТМ БОЙЕРА-МУРА 2. Эвристика стоп-символа. Предположим, что мы производим поиск слова «колокол». Первая же буква не
11. АЛГОРИТМ БОЙЕРА-МУРА Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа не работает. В таких
12. АЛГОРИТМ БОЙЕРА-МУРА Обе эвристики требуют предварительных вычислений — в зависимости от шаблона поиска заполняются две таблицы.
13. АЛГОРИТМ БОЙЕРА-МУРА Таблица суффиксов Для каждого возможного суффикса S шаблона строки указываем наименьшую величину, на которую
14. АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА Этот алгоритм – в общем случае самый быстрый из алгоритмов поиска подстроки в тексте
15. АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА Шаг 1. Построение таблицы префиксов TB. TB – массив целых чисел длиной m. Объявим
16. Пример 1. S=‘арарат’; % 6 букв TB=zeros(1,6); % заполняем нулями таблицу префиксов. TB(1)=0. k=2. S(1:2) =
17. % Matlab % Быстрый алгоритм заполнения таблицы префиксов % для строки S длиной m: TB=zeros(1,m); %
18. Шаг 2. Быстрый поиск подстроки S в тексте T с использованием полученной таблицы префиксов TB, где
19. Пример 123456789012345 T=‘оконокнокнокаон’ n=15 S=‘окнока’ m=6 TB=[0 0 0 1 2 0] j=1. i=1. S(1)==T(1) ?
21. Скачать презентацию

Слайд 2

Поиск подстроки в строке — типичная задача поиска информации. На сегодняшний

день существует огромное разнообразие алгоритмов поиска подстроки. Программисту приходится выбирать подходящий в зависимости от следующих факторов.
Нужна ли вообще оптимизация, или хватает примитивного алгоритма? Как правило, именно его реализуют стандартные библиотеки языков программирования.
«Враждебность» пользователя. Другими словами: будет ли пользователь намеренно задавать данные, на которых алгоритм будет медленно работать?
Грамматика языка может быть недружественной к тем или иным эвристикам, которые ускоряют поиск «в среднем».
Архитектура процессора. Некоторые процессоры имеют автоинкрементные или SIMD-операции, которые позволяют быстро сравнить два участка ОЗУ (например, rep cmpsd на x86).
Размер алфавита. Многие алгоритмы имеют эвристики, связанные с несовпавшим символом. На больших алфавитах таблица символов будет занимать много памяти, на малых — соответствующая эвристика будет неэффективной.
Возможность проиндексировать исходный текст. Если таковая есть, поиск серьёзно ускорится.
Требуется ли одновременный поиск нескольких строк? Приблизительный поиск?

Слайд 3

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

Слайд 4

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

Слайд 5

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

Слайд 6

ЛИНЕЙНЫЙ ПОИСК
Линейный, последовательный поиск (поиск методом полного перебора или брутфорса) —

алгоритм нахождения заданного значения произвольной функции на некотором отрезке.
Данный алгоритм является простейшим алгоритмом поиска и, в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию.
Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило, поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершённым.

Слайд 7

ЛИНЕЙНЫЙ ПОИСК
В связи с малой эффективностью по сравнению с другими алгоритмами

линейный поиск обычно используют, только если отрезок поиска содержит очень мало элементов, тем не менее, линейный поиск не требует дополнительной памяти или обработки/анализа функции, так что может работать в потоковом режиме при непосредственном получении данных из любого источника. Также линейный поиск часто используется в виде линейных алгоритмов поиска максимума/минимума.
Обычно линейный поиск очень прост в реализации и применим, если список содержит мало элементов, либо в случае одиночного поиска в неупорядоченном списке.
Если предполагается в одном и том же списке большое число раз, то часто имеет смысл предварительной обработки списка, например, сортировки и последующего использования бинарного поиска, либо построения какой-либо эффективной структуры данных для поиска. Частая модификация списка также может оказывать влияние на выбор дальнейших действий, поскольку делает необходимым процесс перестройки структуры.

Слайд 8

ЛИНЕЙНЫЙ ПОИСК
Условие: дано два массива A и B. Нужно определить, является

ли массив A подстрокой (фрагментом) массива B?
A = [ 3 5 8 12 3 ];
B = [3 5 17 1 9 3 5 8 12 3 4 9 11 6];
z=length(A)-1;
k=length(B)-z;
for i=1:k
if A==B(i:i+z)
disp(‘Да, является.’);
end
end
Сложность алгоритма - O(n*m), где n и m – длины массивов A и B

Слайд 9

АЛГОРИТМ БОЙЕРА-МУРА
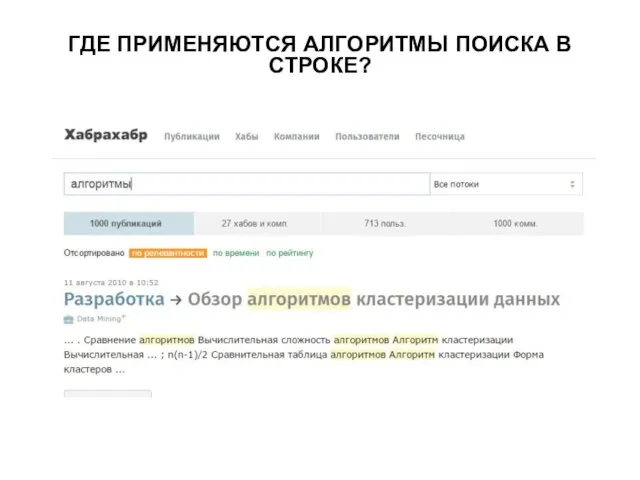
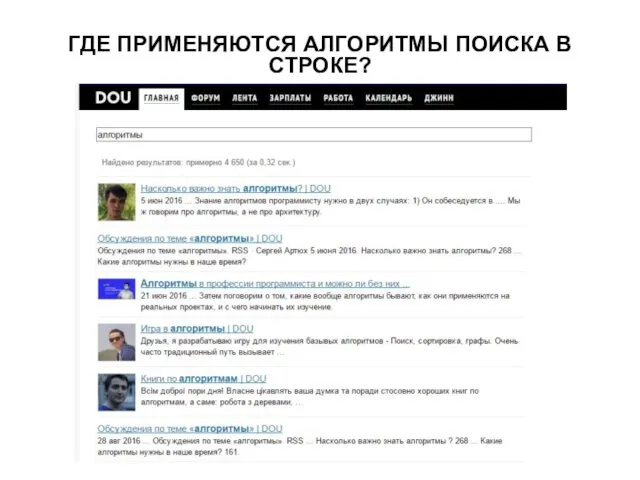
Алгоритм поиска строки Бойера-Мура, считается наиболее быстрым среди алгоритмов общего

назначения, предназначенных для поиска подстроки в строке.
Преимущество этого алгоритма в том, что ценой некоторого количества предварительных вычислений над шаблоном (но не над строкой, в которой ведётся поиск) шаблон сравнивается с исходным текстом не во всех позициях — часть проверок пропускаются как заведомо не дающие результата.
Общая оценка вычислительной сложности алгоритма O(n + m*s) n – алфавит, m – строка, s – шаблон.
Алгоритм основан на трёх идеях.
1. Сканирование слева направо, сравнение справа налево. Совмещается начало текста (строки) и шаблона, проверка начинается с последнего символа шаблона. Если символы совпадают, производится сравнение предпоследнего символа шаблона и т. д. Если все символы шаблона совпали с наложенными символами строки, значит, подстрока найдена, и поиск окончен.
Если же какой-то символ шаблона не совпадает с соответствующим символом строки, шаблон сдвигается на несколько символов вправо, и проверка снова начинается с последнего символа.

Слайд 10

АЛГОРИТМ БОЙЕРА-МУРА
2. Эвристика стоп-символа. Предположим, что мы производим поиск слова «колокол».

Первая же буква не совпала — «к» (назовём эту букву стоп-символом). Тогда можно сдвинуть шаблон вправо до последней его буквы «к».
Если стоп-символа в шаблоне вообще нет, шаблон смещается за этот стоп-символ.
В данном случае стоп-символ — «а», и шаблон сдвигается так, чтобы он оказался прямо за этой буквой. В алгоритме Бойера-Мура эвристика стоп-символа вообще не смотрит на совпавший суффикс, так что первая буква шаблона («к») окажется под «л», и будет проведена одна заведомо холостая проверка. Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа не работает.

Слайд 11

АЛГОРИТМ БОЙЕРА-МУРА
Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа

не работает.
В таких ситуациях выручает третья идея АБМ — эвристика совпавшего суффикса.
3. Эвристика совпавшего суффикса. Если при сравнении строки и шаблона совпало один или больше символов, шаблон сдвигается в зависимости от того, какой суффикс совпал.
В данном случае совпал суффикс «окол», и шаблон сдвигается вправо до ближайшего «окол». Если подстроки «окол» в шаблоне больше нет, но он начинается на «кол», сдвигается до «кол», и т. д.

Слайд 12

АЛГОРИТМ БОЙЕРА-МУРА
Обе эвристики требуют предварительных вычислений — в зависимости от шаблона

поиска заполняются две таблицы. Таблица стоп-символов по размеру соответствует алфавиту (например, если алфавит состоит из 256 символов, то её длина 256); таблица суффиксов — искомому шаблону. Именно из-за этого алгоритм Бойера-Мура не учитывает совпавший суффикс и несовпавший символ одновременно — это потребовало бы слишком много предварительных вычислений.
Опишем подробнее обе таблицы.
Таблица стоп-символов
В таблице стоп-символов указывается последняя позиция из строки (исключая последнюю букву) каждого из символов алфавита. Для всех символов, не вошедших в строку пишем 0. Например, если строка = «abcdadcd» , таблица стоп-символов будет выглядеть так

Слайд 13

АЛГОРИТМ БОЙЕРА-МУРА
Таблица суффиксов
Для каждого возможного суффикса S шаблона строки указываем наименьшую величину, на которую нужно

сдвинуть вправо шаблон, чтобы он снова совпал с S. Например, для той же строки «abcdadcd» будет:

Слайд 14

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА
Этот алгоритм – в общем случае самый быстрый из алгоритмов

поиска подстроки в тексте (на практике алгоритм Боуера-Мура иногда бывает быстрее).
Вычислительная сложность алгоритма равна O(m+n), где m – длина подстроки S, а n – длина текста T. Время работы алгоритма линейно зависит от объёма входных данных, то есть разработать асимптотически более эффективный алгоритм невозможно.
Даны образец (строка) S и строка T. Требуется определить индекс, начиная с которого образец S содержится в строке T. Если S не содержится в T вернуть индекс, который не может быть интерпретирован как позиция в строке (например, отрицательное число). При необходимости отслеживать каждое вхождение образца в текст имеет смысл завести дополнительную функцию, вызываемую при каждом обнаружении образца.

Слайд 15

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА
Шаг 1. Построение таблицы префиксов TB. TB – массив целых

чисел длиной m. Объявим его (здесь и далее - синтаксис Матлаба) как TB=zeros(1,m);
Алгоритм построения таблицы префиксов.
Для первой буквы полагаем TB(1)=0;
Для каждого k от 2 до m находим максимальное j, при котором префикс S(1:j) совпадает с суффиксом S(k-j+1:k). Записываем полученное значение j в TB:
TB(k)=j;

Слайд 16

Пример 1.
S=‘арарат’; % 6 букв
TB=zeros(1,6); % заполняем нулями таблицу префиксов. TB(1)=0.
k=2. S(1:2)

= ‘ар’.
Никакой префикс не совпадает с суффиксом. j=0, TB(2)=0.
k=3. S(1:3)=‘ара’.
Префикс ‘а’ совпадает с суффиксом ‘a’. j=1 (длина совпадения). TB(3)=1.
k=4. S(1:4)=‘арар’;
Префикс ‘ар’ совпадает с суффиксом ‘ар’. j=2. TB(4)=2.
k=5. S(1:5)=‘арара’;
Префикс ‘ара’ совпадает с суффиксом ‘aра’. j=3 (длина совпадения). TB(5)=3.
k=6. S(1:6)=‘арарат’;
Никакой префикс не совпадает с суффиксом. j=0, TB(6)=0.
TB = [ 0 0 1 2 3 0 ];

Слайд 17

% Matlab
% Быстрый алгоритм заполнения таблицы префиксов % для строки S

длиной m:
TB=zeros(1,m); % TB(1) здесь уже равно 0
j=0;
for k=2:m
while (j>0)&(S(k)~=S(1+j))
j=TB(j);
end
if S(k)==S(1+j)
j=j+1;
end
TB(k)=j;
end

Слайд 18

Шаг 2. Быстрый поиск подстроки S в тексте T с использованием

полученной таблицы префиксов TB, где m – длина S, а n – длина T.
Алгоритм:
j=1; i=1;
Если S(j) == T(i) то перейти на шаг 3, иначе перейти на шаг 6.
i=i+1; j=j+1;
Если j>m, значит подстрока в тексте найдена и алгоритм заканчивает работу. Иначе – перейти на шаг 5.
Если i>n, значит в тексте вообще нет этой подстроки и алгоритм заканчивает работу. Иначе – перейти на шаг 2.
Если j==1, то i=i+1 и перейти на шаг 2, иначе – на шаг 7.
j=TB(j-1)+1. Перейти на шаг 2.

Слайд 19

Пример
123456789012345
T=‘оконокнокнокаон’ n=15
S=‘окнока’ m=6
TB=[0 0 0 1 2 0]
j=1. i=1.
S(1)==T(1) ? j=2.

i=2. S(5)==T(9) ? j=6. i=10.
S(2)==T(2) ? j=3. i=3. S(6)~=T(10)? j=TB(6-1)+1=3
S(3)~=T(3) ? j=TB(3-1)+1=1. S(3)==T(10)? j=4. i=11.
S(1)==T(3) ? j=2. i=4. S(4)==T(11)? j=5. i=12.
S(2)~=T(4) ? j=TB(2-1)+1=1. S(5)==T(12)? j=6. i=13.
S(1)~=T(4) ? j==1 ? i=5. S(6)==T(13)? j=7. i=14.
S(1)==T(5) ? j=2. i=6. j>m ? подстрока найдена
S(2)==T(6) ? j=3. i=7. в позиции i-m = 8
S(3)==T(7) ? j=4. i=8.
S(4)==T(8) ? j=5. i=9.

Алгоритмы поиска в строке

Содержание

Поиск подстроки в строке — типичная задача поиска информации. На сегодняшний

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

ГДЕ ПРИМЕНЯЮТСЯ АЛГОРИТМЫ ПОИСКА В СТРОКЕ?

ЛИНЕЙНЫЙ ПОИСКЛинейный, последовательный поиск (поиск методом полного перебора или брутфорса) —

ЛИНЕЙНЫЙ ПОИСКВ связи с малой эффективностью по сравнению с другими алгоритмами

ЛИНЕЙНЫЙ ПОИСКУсловие: дано два массива A и B. Нужно определить, является

АЛГОРИТМ БОЙЕРА-МУРААлгоритм поиска строки Бойера-Мура, считается наиболее быстрым среди алгоритмов общего

АЛГОРИТМ БОЙЕРА-МУРА2. Эвристика стоп-символа. Предположим, что мы производим поиск слова «колокол».

АЛГОРИТМ БОЙЕРА-МУРАЕсли стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа

АЛГОРИТМ БОЙЕРА-МУРАОбе эвристики требуют предварительных вычислений — в зависимости от шаблона

АЛГОРИТМ БОЙЕРА-МУРАТаблица суффиксовДля каждого возможного суффикса S шаблона строки указываем наименьшую величину, на которую нужно

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТАЭтот алгоритм – в общем случае самый быстрый из алгоритмов

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТАШаг 1. Построение таблицы префиксов TB. TB – массив целых

Пример 1.S=‘арарат’; % 6 буквTB=zeros(1,6); % заполняем нулями таблицу префиксов. TB(1)=0.k=2. S(1:2)

% Matlab% Быстрый алгоритм заполнения таблицы префиксов % для строки S

Шаг 2. Быстрый поиск подстроки S в тексте T с использованием

Пример 123456789012345T=‘оконокнокнокаон’ n=15S=‘окнока’ m=6TB=[0 0 0 1 2 0]j=1. i=1. S(1)==T(1) ? j=2.

Похожие презентации

ЛИНЕЙНЫЙ ПОИСК
Линейный, последовательный поиск (поиск методом полного перебора или брутфорса) —

ЛИНЕЙНЫЙ ПОИСК
В связи с малой эффективностью по сравнению с другими алгоритмами

ЛИНЕЙНЫЙ ПОИСК
Условие: дано два массива A и B. Нужно определить, является

АЛГОРИТМ БОЙЕРА-МУРА
Алгоритм поиска строки Бойера-Мура, считается наиболее быстрым среди алгоритмов общего

АЛГОРИТМ БОЙЕРА-МУРА
2. Эвристика стоп-символа. Предположим, что мы производим поиск слова «колокол».

АЛГОРИТМ БОЙЕРА-МУРА
Если стоп-символ «к» оказался за другой буквой «к», эвристика стоп-символа

АЛГОРИТМ БОЙЕРА-МУРА
Обе эвристики требуют предварительных вычислений — в зависимости от шаблона

АЛГОРИТМ БОЙЕРА-МУРА
Таблица суффиксов
Для каждого возможного суффикса S шаблона строки указываем наименьшую величину, на которую нужно

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА
Этот алгоритм – в общем случае самый быстрый из алгоритмов

АЛГОРИТМ КНУТА-МОРРИСА-ПРАТТА
Шаг 1. Построение таблицы префиксов TB. TB – массив целых

Пример 1.
S=‘арарат’; % 6 букв
TB=zeros(1,6); % заполняем нулями таблицу префиксов. TB(1)=0.
k=2. S(1:2)

% Matlab
% Быстрый алгоритм заполнения таблицы префиксов % для строки S

Пример
123456789012345
T=‘оконокнокнокаон’ n=15
S=‘окнока’ m=6
TB=[0 0 0 1 2 0]
j=1. i=1.
S(1)==T(1) ? j=2.