Содержание
- 2. Дерево поиска Дерево, дерево с корнем. Высота дерева. Родительские и дочерние узлы, листья. Количество рёбер
- 3. Количество деревьев с пронумерованными вершинами Теорема Кэли Число деревьев на n вершинах, пронумерованных от 1 до
- 4. Код Прюфера Кодирование производится через последовательное удаление вершин дерева, имеющих наименьший номер и являющихся концевыми. При
- 5. Код Прюфера Любое дерево естественно переводится в Код Прюфера. Код имеет размер (n-2), всего кодов на
- 6. Обход в глубину Для бинарных деревьев -- pre-, post- и in-order
- 7. Обход в ширину
- 8. Деревья поиска Поиск ключа, вставка, удаление Необходимость балансировки
- 9. АВЛ-дерево Хотим поддерживать разницу между поддеревьями любой вершины |h(L)-h(R)| Для этого в процессе проведения операций будем
- 10. АВЛ-дерево
- 11. АВЛ-дерево Добавление элемента: сначала идём вниз от корня как при поиске, пока не дойдём до отсутствующей
- 12. АВЛ-дерево Удаление вершины. Если вершина -- лист, то просто удаляем. Если внутренняя, то найдём ближайшую по
- 13. Слияние двух АВЛ-деревьев Пусть есть деревья X и Y, все ключи X Пусть высота X меньше,
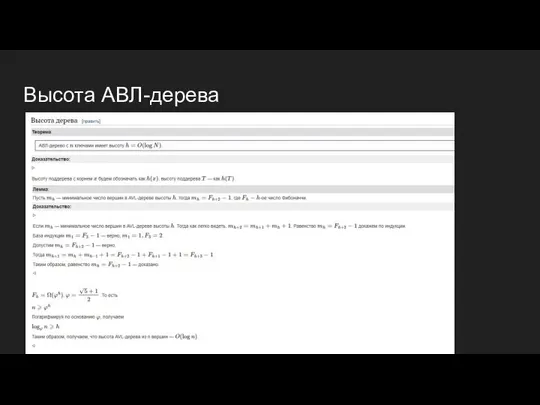
- 14. Высота АВЛ-дерева
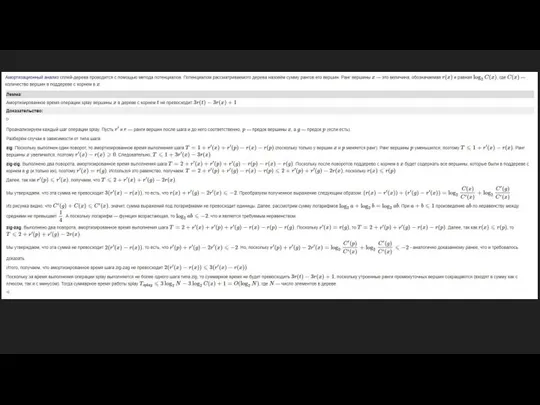
- 15. Сплей-дерево Дерево, позволяющее получать быстрый доступ к элементам, которые были использованы последними
- 16. Эвристики moveToRoot(x) -- совершает повороты (x,p), где х -- вершина, p -- её предок, пока x
- 17. Операции над сплей-деревом merge -- запускаем splay от самого большого элемента X, подвешиваем справа Y (
- 19. Декартово дерево поиска -- хранит элементы (x,y), где x -- ключ, а y -- приоритет. Декартово
- 20. Операции над декартовым деревом split(x): пусть x больше корня, тогда в левом дереве окажется левое поддерево
- 21. Операции над декартовым деревом insert(x) -- разделим дерево по x, а потом сольём сначала T1 и
- 22. Построение По очереди вставим все элементы Пусть элементы отсортированы по возрастанию ключей. Смотрим на самый правый
- 23. Высота декартова дерева Теорема. В декартовом дереве на n узлов, у которого приоритеты -- равномерно распределённые
- 24. Красно-чёрное дерево Дерево поиска, вершины которого промаркированы определённым цветом: красным или чёрным Каждая вершина — либо
- 25. Высота красно-чёрного дерева Чёрная высота x -- количество чёрных вершин на пути из х в лист
- 26. Высота красно-чёрного дерева Лемма. Высота красно-чёрного дерева с N вершинами равна O(logn) Количество красных вершин не
- 27. Вставка элемента Идём от корня до листа по условиям деревья поиска. Вставляем вершину с красным цветом.
- 28. Удаление элемента Три варианта: Мы в листе -- изменяем указатель родителя на nul Есть один ребёнок
- 29. B-дерево
- 30. Операции над B-деревом
- 31. KD-дерево
- 33. Скачать презентацию


























 Величини логічного типу, операції над ними. Алгоритми з розгалуженнями для опрацювання величин
Величини логічного типу, операції над ними. Алгоритми з розгалуженнями для опрацювання величин Matlab
Matlab Специальные возможности числового редактора MS Excel
Специальные возможности числового редактора MS Excel Операции над высказываниями
Операции над высказываниями Инфографика. Визуализация
Инфографика. Визуализация Хранилища многомерных данных (Data Warehouse)
Хранилища многомерных данных (Data Warehouse) Искусственный интеллект
Искусственный интеллект Презентация "Графический интерфейс операционных систем и приложений" - скачать презентации по Информатике
Презентация "Графический интерфейс операционных систем и приложений" - скачать презентации по Информатике Виды базы данных
Виды базы данных Использование локальных учебных программных модулей для обучения началам статистики
Использование локальных учебных программных модулей для обучения началам статистики PowerPoint В этой презентации я продемонстрирую умения в использовании программой PowerPoint.
PowerPoint В этой презентации я продемонстрирую умения в использовании программой PowerPoint. Руководитель: учитель математики Воронкова О.И. Автор : ученик 8в класса Каптюшин Михаил Мате
Руководитель: учитель математики Воронкова О.И. Автор : ученик 8в класса Каптюшин Михаил Мате Системы счисления
Системы счисления Файлы и файловая структура
Файлы и файловая структура Одномерные массивы целых чисел. Последовательный поиск элементов в массиве. Алгоритмизация и программирование
Одномерные массивы целых чисел. Последовательный поиск элементов в массиве. Алгоритмизация и программирование Организация строительного портала по BIM-модели
Организация строительного портала по BIM-модели Системное тестирование ПО
Системное тестирование ПО Базы данных. Реляционная база данных
Базы данных. Реляционная база данных Firmware update process-easy version
Firmware update process-easy version Формирование УУД на занятиях Робототехника. Модернизация
Формирование УУД на занятиях Робототехника. Модернизация Стандартизация информационных технологий в Республике Беларусь. Единая система программной документации (ЕСПД)
Стандартизация информационных технологий в Республике Беларусь. Единая система программной документации (ЕСПД) Информационные модели
Информационные модели Analysis and Data Management. Lecture 6
Analysis and Data Management. Lecture 6 Современные процессоры Intel и AMD
Современные процессоры Intel и AMD  Cs 5220: computer communications
Cs 5220: computer communications Презентация в обучении Цель Предмет Место на уроке Создание в Power Point Эффекты анимации
Презентация в обучении Цель Предмет Место на уроке Создание в Power Point Эффекты анимации Презентация Операторы ветвления
Презентация Операторы ветвления СУБД Access. Создание главной кнопочной формы
СУБД Access. Создание главной кнопочной формы