Содержание
- 2. Ограничение на эвристики Допустимость h(v) -- для любой вершины эвристика не превосходит реальное кратчайшее расстояние Монотонность
- 3. Остовные деревья
- 4. Остовное дерево Ациклический связный подграф, включающий все вершины графа. Как найти?
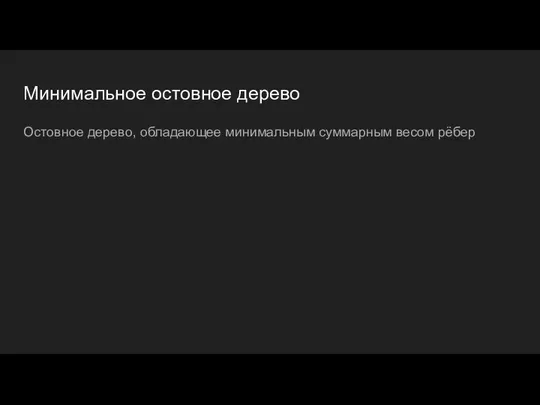
- 5. Минимальное остовное дерево Остовное дерево, обладающее минимальным суммарным весом рёбер
- 6. Лемма о безопасном ребре Пусть G’ -- подграф миностова G Ребро не из G’ -- безопасное,
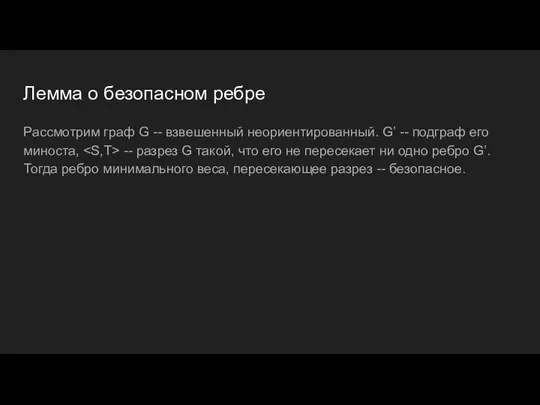
- 7. Лемма о безопасном ребре Рассмотрим граф G -- взвешенный неориентированный. G’ -- подграф его миноста, --
- 8. Алгоритм Прима Похож на Дейкстру Пытаемся построить миностов, начиная с любой вершины. Когда есть несколько вершин
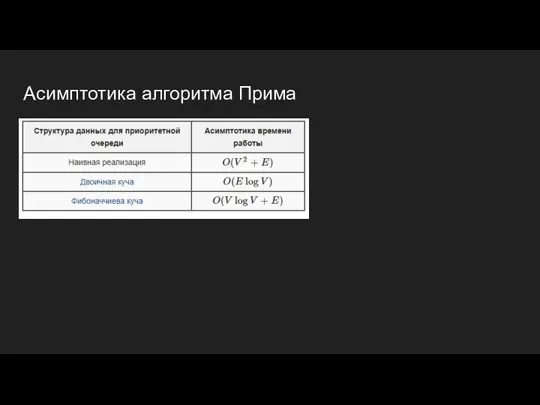
- 9. Асимптотика алгоритма Прима
- 10. Алгоритм Крускала Отсортируем все рёбра в порядке возрастания и будем последовательно добавлять в остов. Если ребро
- 11. Система непересекающихся множеств Каждое множество -- дерево, корень -- его “представитель”. В каждой вершине -- ссылка
- 12. Эвристики СНМ Объединение по рангу. Подвешиваем дерево с меньшей высотой к дереву с большей. Чтобы не
- 13. Асимптотика алгоритма Крускала Сортировка рёбер -- O(ElogE) СНМ -- O(E*alpha(V)) Общая асимптотика -- O(ElogE)
- 14. Алгоритм Борувки Каждая вершина графа -- дерево Для каждого дерева найдём минимальноe инцидентное ему ребро. Добавим
- 15. Алгоритм Борувки. Асимптотика На каждом шаге количество деревьев сокращается как минимум вдвое. То есть шагов --
- 16. Максимальный поток в сети. RMQ & LCA
- 17. Определение сети и потока Сеть -- орграф, с:E->R+, с(e) -- пропускная способность. В сети есть исток
- 18. Разрез. Поток через разрез Разрез -- знаем Пропускная способность разреза -- сумма всех рёбер, пересекающих разрез
- 19. Лемма о величине потока f(S,T) = |f|
- 20. Лемма о минимальном разрезе Если f(S,T) = c(S,T), то поток f максимален, а разрез -- минимален
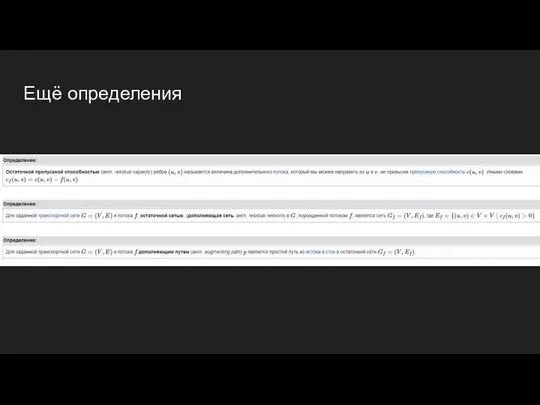
- 21. Ещё определения
- 22. Теорема Форда-Фалкерсона Если f -- поток в сети G = (V,E), то следующие утверждения эквивалентны: Поток
- 23. Алгоритм Форда-Фалкерсона Положим f(u,v) = 0 Далее поток увеличивается итеративно через поиск увеличивающего пути Поиск можно
- 24. Алгоритм Эдмонса-Карпа Улучшение алгоритма Форда-Фалкерсона, в качестве дополняющего пути берём кратчайший по рёбрам Асимптотика O(VE^2) Найти
- 25. Алгоритм Диница Слоистая сеть Определим для каждой вершины v длину кратчайшего s->v. В слоистую сеть включаем
- 26. Поиск блокирующего потока Можно просто искать все пути s->t по одному и наполнять(по крайней мере одно
- 27. Алгоритм Диница Инициализируем f(u,v) = 0 Построим вспомогательную сеть для остаточной данного графа. Если пустая --
- 28. Паросочетания Паросочетание -- набор попарно несмежных рёбер в двудольном графе. Максимальное паросочетание -- паросочетание с наибольшим
- 29. Теорема Бержа Паросочетание максимально тогда и только тогда, когда не существует увеличивающих относительно него цепей. Пусть
- 30. Теорема Бержа Пусть парсоч M не содержит ув. пути, но есть парсоч M’, который больше чем
- 31. Алгоритм Куна поиска паросочетаний Возьмём пустое паросочетание, пока в графе находим увеличивающую цепь -- выполняем “чередование”
- 32. Алгоритм Куна Возьмём пустое паросочетание Пока удаётся найти увеличивающую цепь -- выполняем чередование Массив matching[v] --
- 34. Скачать презентацию



























 Презентация "Создание реляционной БД в среде СУБД ACCESS" - скачать презентации по Информатике
Презентация "Создание реляционной БД в среде СУБД ACCESS" - скачать презентации по Информатике Информационные процессы
Информационные процессы Single-row functions
Single-row functions Презентация "Компьютерное тестирование. Основные понятия и виды компьютерного тестирования" - скачать презентации по Информ
Презентация "Компьютерное тестирование. Основные понятия и виды компьютерного тестирования" - скачать презентации по Информ Дидактический материал по информатике для начальной школы Птицына Светлана Васильевна, учитель начальных классов МОУ СОШ № 8 г.
Дидактический материал по информатике для начальной школы Птицына Светлана Васильевна, учитель начальных классов МОУ СОШ № 8 г. Компьютерная безопасность
Компьютерная безопасность Как составить резюме, сопроводительное и мотивационное письмо
Как составить резюме, сопроводительное и мотивационное письмо Telegram News концепция
Telegram News концепция Перевод двоичных чисел в десятичную систему счисления
Перевод двоичных чисел в десятичную систему счисления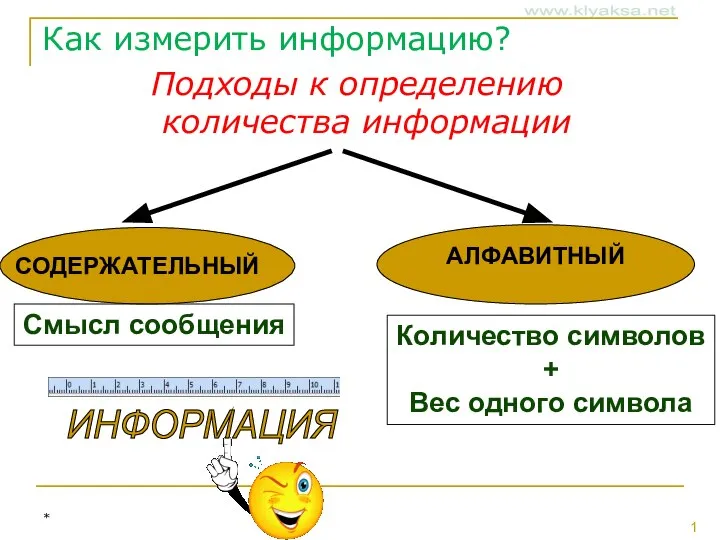 Подходы к определению количества информации
Подходы к определению количества информации Информация, её виды и свойства
Информация, её виды и свойства Проект: календарь. Индивидуальный образ настенного календаря
Проект: календарь. Индивидуальный образ настенного календаря Электронная коммерция в Интернете Саранцева О.Н. учитель информатики и ИКТ МОУ СОШ №1 г. Спасска Пензенской области
Электронная коммерция в Интернете Саранцева О.Н. учитель информатики и ИКТ МОУ СОШ №1 г. Спасска Пензенской области  Школа программирования: проект по открытию IT классов на базе детских садов и школ
Школа программирования: проект по открытию IT классов на базе детских садов и школ Средства разработки презентаций. Назначение и возможности Power Point
Средства разработки презентаций. Назначение и возможности Power Point Способы представления синтаксической структуры высказывания. (Лекция 4)
Способы представления синтаксической структуры высказывания. (Лекция 4) Элементы компьютерной математики. (Лекция 7)
Элементы компьютерной математики. (Лекция 7) Решение задач на компьютере алгоритмизация и программирование
Решение задач на компьютере алгоритмизация и программирование Оптимизация написания верстки
Оптимизация написания верстки Определение ключевых полей
Определение ключевых полей Курс таро он-лайн Колесо фортуны
Курс таро он-лайн Колесо фортуны Технологии виртуальной и дополненной реальности
Технологии виртуальной и дополненной реальности Измерение объёма текстовой информации
Измерение объёма текстовой информации Обмен данными в Windows
Обмен данными в Windows Монитор
Монитор  Автомат Мили
Автомат Мили Презентация "Базы данных 10" - скачать презентации по Информатике
Презентация "Базы данных 10" - скачать презентации по Информатике История ЭВМ презентация
История ЭВМ презентация