Содержание
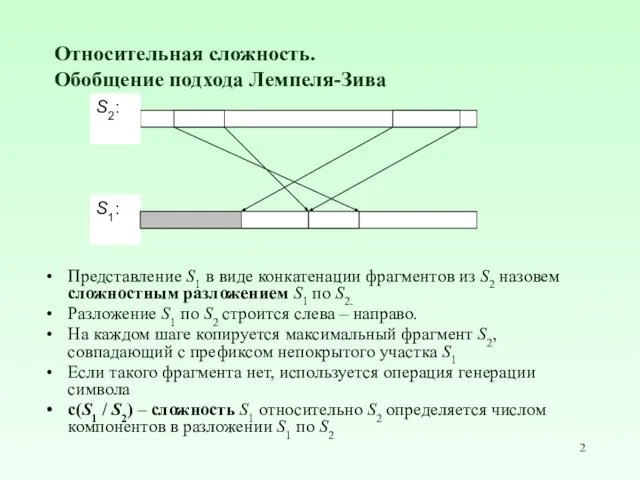
- 2. Относительная сложность. Обобщение подхода Лемпеля-Зива Представление S1 в виде конкатенации фрагментов из S2 назовем сложностным разложением
- 3. Относительная сложность и редакционное расстояние S2 = aaaa a cccc c ttttttttttttt – acacacac a atatatat
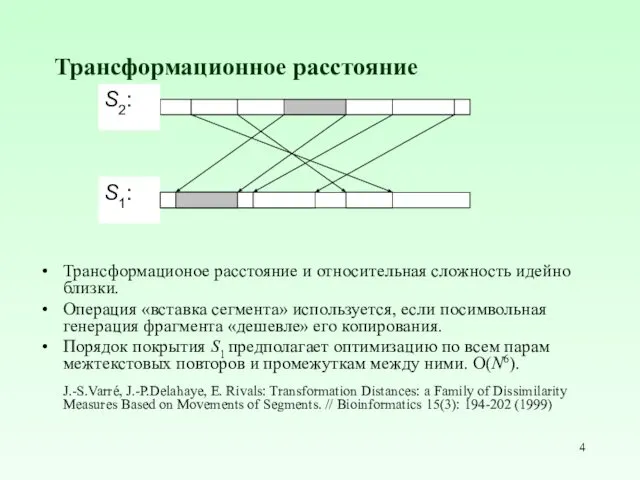
- 4. Трансформационное расстояние Трансформационое расстояние и относительная сложность идейно близки. Операция «вставка сегмента» используется, если посимвольная генерация
- 5. Инверсионное расстояние Инверсионное расстояние dI(π,σ) между последовательностями π и σ определяется минимальным числом инверсий, переводящих одну
- 6. Точки разрыва π0 = 0 and πN+1 = N + 1 π and σ − произвольные
- 7. Инверсионное расстояние, число точек разрыва и относительная сложность r(π,σ) ≤ 2dI(π,σ) Точки разрыва однозначно соответствуют границам
- 8. Phylogenetic trees for 65 species of the genus Chironomus
- 9. Расстояния и меры сходства, отличные от ред. расстояния Пусть T1 и T2 два текста. Назовем совместной
- 10. Мера сходства, учитывающая частоты встречаемости подслов: α – произвольная цепочка символов из текстов T1 и/или T2,
- 11. Ранговые меры близости. Коэффициент корреляции τ
- 12. Ранговые меры близости. Коэффициент корреляции τ
- 13. Ранговые меры близости. Коэффициент корреляции τ Пусть l-граммы в Φ l(T1) и Φ l(T2) упорядочены по
- 14. Ранговые меры близости. Коэффициент Спирмэна
- 16. Скачать презентацию











 Как устроена компьютерная сеть
Как устроена компьютерная сеть Презентация "Текстовый процессор Microsoft Word" - скачать презентации по Информатике
Презентация "Текстовый процессор Microsoft Word" - скачать презентации по Информатике Influence of video resolution on its Youtube search result ranking tested out by SeeZisLab
Influence of video resolution on its Youtube search result ranking tested out by SeeZisLab Оптимизация РСЯ – не танцы с бубном
Оптимизация РСЯ – не танцы с бубном Алгоритмическая конструкция следование. Основные алгоритмические конструкции
Алгоритмическая конструкция следование. Основные алгоритмические конструкции Презентация "Водяная система охлаждения" - скачать презентации по Информатике
Презентация "Водяная система охлаждения" - скачать презентации по Информатике Вычисление НОД. Программирование на алгоритмическом языке
Вычисление НОД. Программирование на алгоритмическом языке Программирование на языке Паскаль. Алфавит языка
Программирование на языке Паскаль. Алфавит языка 2ГИС Сервис. Все площадки (КП для клиента)
2ГИС Сервис. Все площадки (КП для клиента) Информатика, скакалочка
Информатика, скакалочка Общая архитектура FORIS OSS
Общая архитектура FORIS OSS PowerShell: Познать за 9 часов
PowerShell: Познать за 9 часов Administration. Data administration functions
Administration. Data administration functions Презентация на тему "Устройства ввода информации"
Презентация на тему "Устройства ввода информации" Архивация файлов
Архивация файлов Принятие решений голосованием
Принятие решений голосованием Презентация "Типовая корпоративная сеть, понятие уязвимости и атаки - 1" - скачать презентации по Информатике
Презентация "Типовая корпоративная сеть, понятие уязвимости и атаки - 1" - скачать презентации по Информатике Цифровизация государственного управления
Цифровизация государственного управления Модели жизненного цикла. Прикладное программирование
Модели жизненного цикла. Прикладное программирование Lua data types
Lua data types Разработка и эксплуатация клиентской части
Разработка и эксплуатация клиентской части Схема регулирования закупок за счет собственных средств. Постановления Совета Министров Республики Беларусь от 15.03.2012 № 229
Схема регулирования закупок за счет собственных средств. Постановления Совета Министров Республики Беларусь от 15.03.2012 № 229 Массивы в C++
Массивы в C++ Моя школа - новая школа Кубани - Презентация_
Моя школа - новая школа Кубани - Презентация_ ОКСИОН - Общероссийская Комплексная Система Информирования и Оповещения Населения
ОКСИОН - Общероссийская Комплексная Система Информирования и Оповещения Населения Технологія виробництва м’ясних виробів у ковбасному цеху ТОВ Верест м. Дунаївці з введенням цеху напівфабрикатів
Технологія виробництва м’ясних виробів у ковбасному цеху ТОВ Верест м. Дунаївці з введенням цеху напівфабрикатів Привлечение аудитории в Instagram
Привлечение аудитории в Instagram Алгоритмы и исполнители
Алгоритмы и исполнители