Сбалансированные поисковые деревья

ФПМИ БГУ

Изобретателем красно-чёрного дерева считают немецкого учёного:

ФПМИ БГУ

В 1978 году в статье  Л. Гибаса и Р. Седжвика 
структура данных

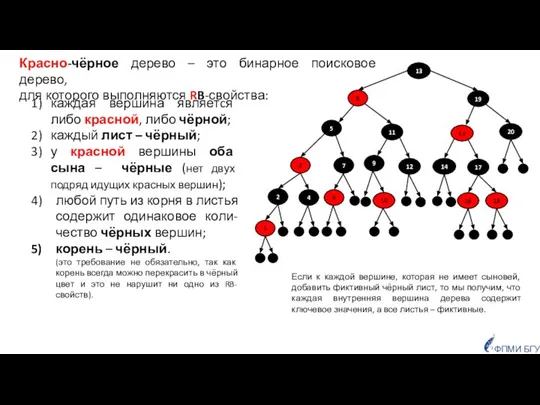
ФПМИ БГУ

Красно-чёрное дерево
является примером сбалансированного поискового дерева
специальные операции балансировки гарантируют,

ФПМИ БГУ

13

8

19

5

15

20

11

9

7

12

2

17

14

4

10

3

1

1

1

1

1

1

1

1

1

1

6

18

16

1

1

1

1

1

1

1

1

1

1

1

1

каждая вершина являетcя либо красной, либо чёрной;
каждый лист – чёрный;
у

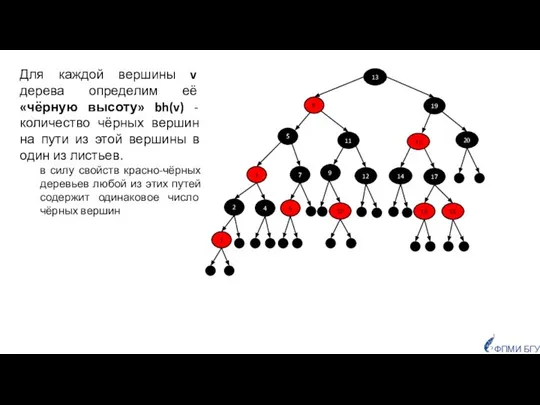
ФПМИ БГУ

Для каждой вершины v дерева определим её «чёрную высоту» bh(v)

ФПМИ БГУ

Используя метод математической индукции (от корня к листьям) можно доказать,

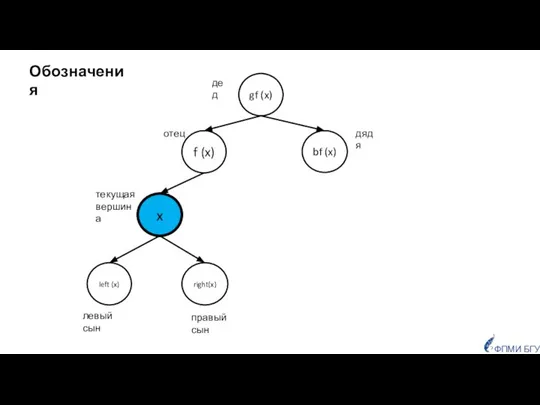
left (x)

right(x)

x

f (x)

gf (x)

bf (x)

отец

дядя

дед

левый сын

правый сын

ФПМИ БГУ

текущая
вершина

Обозначения

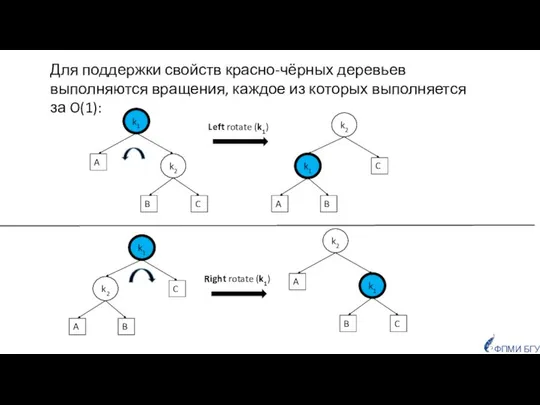
ФПМИ БГУ

Для поддержки свойств красно-чёрных деревьев выполняются вращения, каждое из которых

Добавление вершины в дерево

Осуществляем поиск места для добавляемой вершины x по

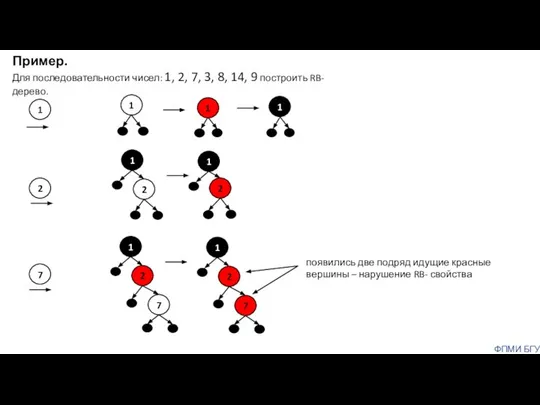
ФПМИ БГУ

1

2

7

Пример.
Для последовательности чисел: 1, 2, 7, 3, 8, 14,

ФПМИ БГУ

Процедуры, восстанавливающие RB-свойства:
(1) перекраски
(2) вращения

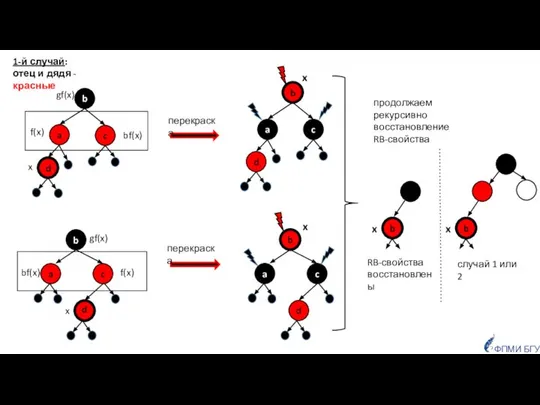
ФПМИ БГУ

RB-свойства
восстановлены

случай 1 или 2

1-й случай:
отец и дядя - красные

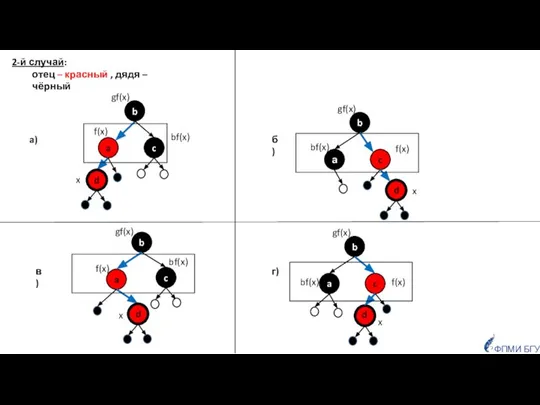
ФПМИ БГУ

bf(x)

a)

в)

2-й случай:
отец – красный , дядя – чёрный

gf(x)

б)

г)

x

x

b

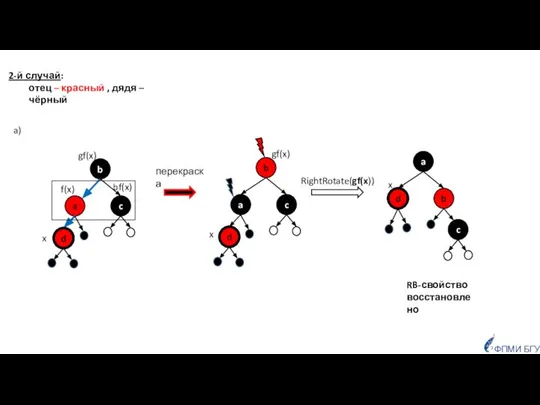
ФПМИ БГУ

bf(x)

a)

RB-свойство
восстановлено

2-й случай:
отец – красный , дядя – чёрный

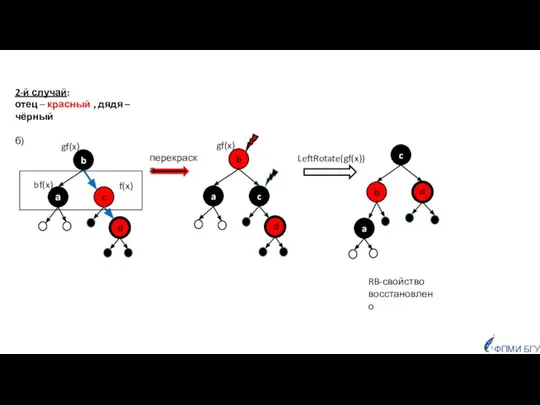
ФПМИ БГУ

RB-свойство
восстановлено

2-й случай:
отец – красный , дядя – чёрный
б)

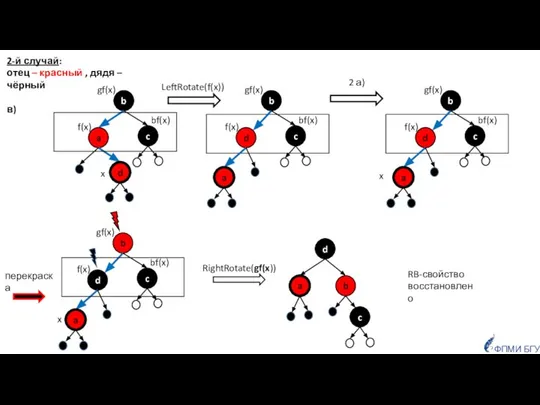
ФПМИ БГУ

2-й случай:
отец – красный , дядя – чёрный
в)

x

x

RB-свойство
восстановлено

2

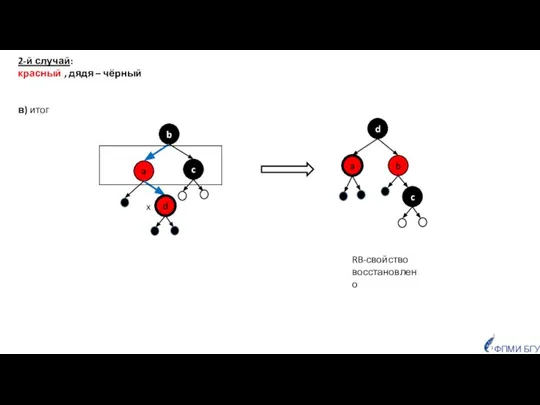
ФПМИ БГУ

RB-свойство
восстановлено

2-й случай:
красный , дядя – чёрный
в) итог

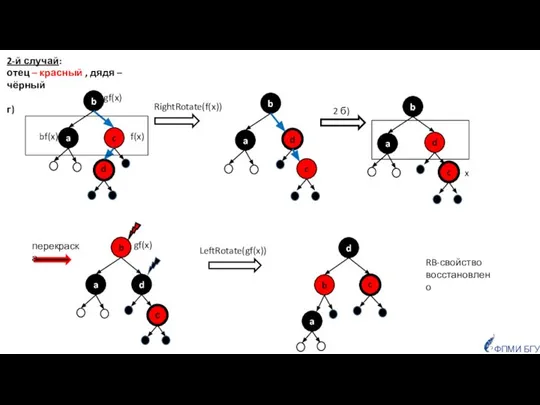
ФПМИ БГУ

gf(x)

2-й случай:
отец – красный , дядя – чёрный
г)

RB-свойство
восстановлено

2

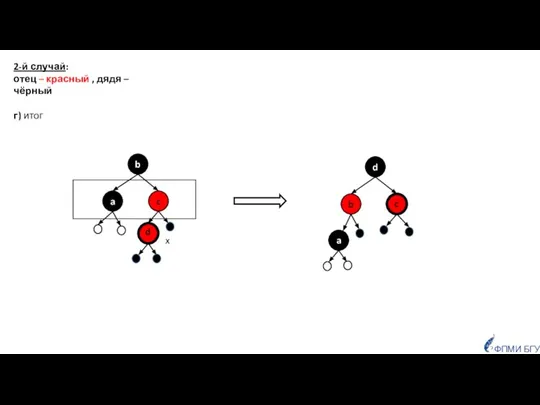
ФПМИ БГУ

2-й случай:
отец – красный , дядя – чёрный
г)

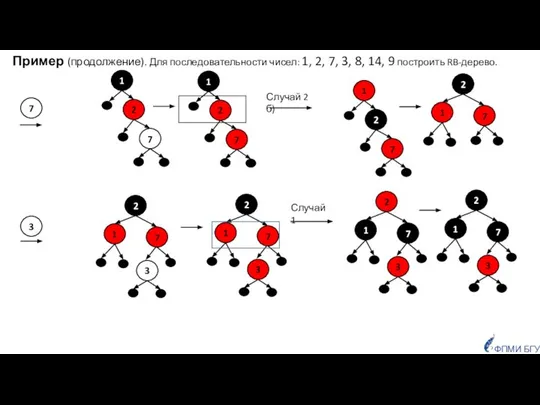
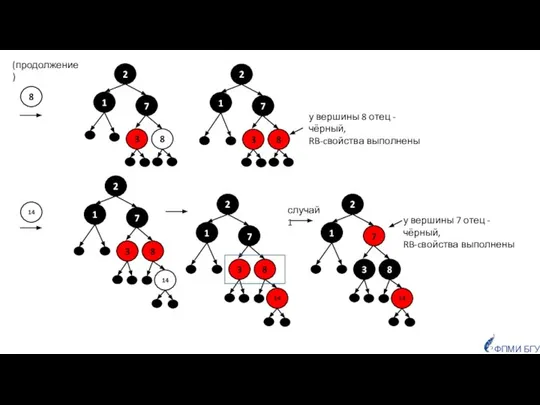
ФПМИ БГУ

7

Пример (продолжение). Для последовательности чисел: 1, 2, 7, 3, 8,

ФПМИ БГУ

(продолжение)

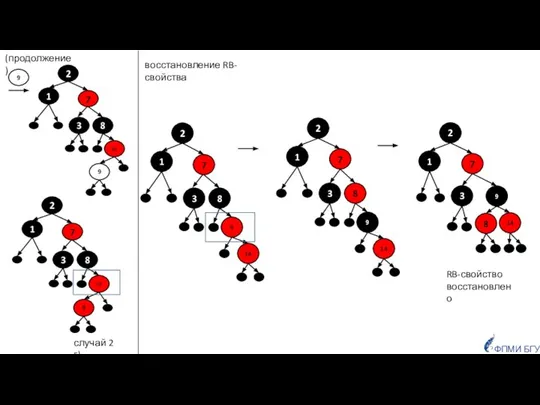
ФПМИ БГУ

случай 2 г)

RB-свойство
восстановлено

(продолжение)

восстановление RB-свойства

Добавление элемента. Оценки.

ФПМИ БГУ

поиск отца – O(log n)
добавление – O(1)
перекрашивания –

Удаление

Удаляем вершину из дерева по аналогии с тем, как это делали

ФПМИ БГУ

y – фактически удалённая вершина
x – единственный ребёнок вершины y

Если фактически удалённая вершина y имела черный цвет, то любой путь,

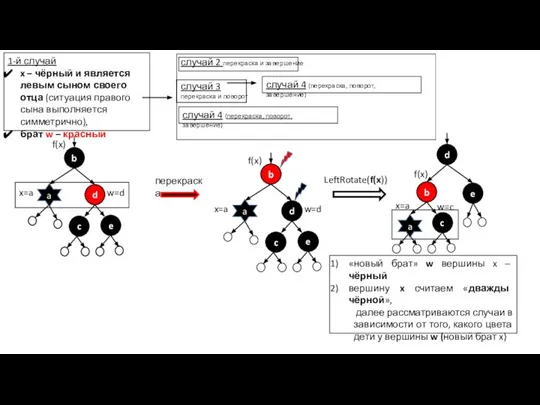
1-й случай
x – чёрный и является левым сыном своего отца

x – «дважды чёрный» и является левым сыном своего отца,
w,

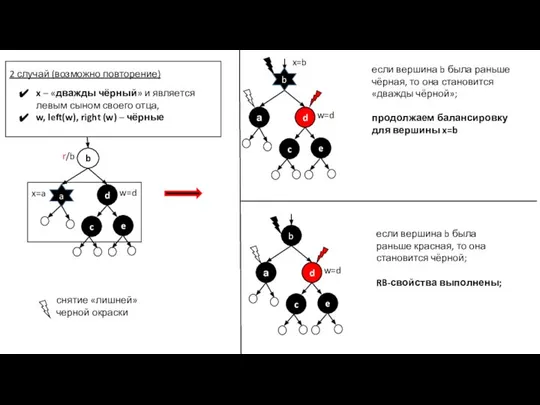
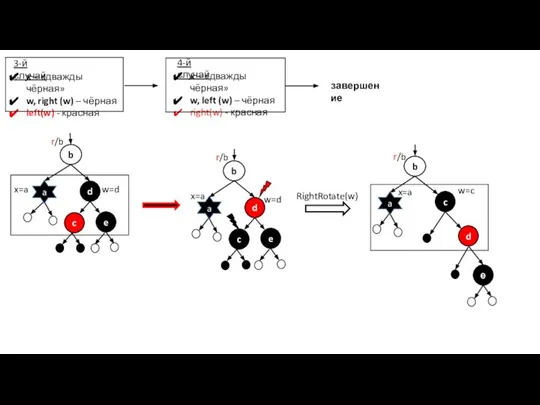
x – «дважды чёрная»
w, right (w) – чёрная
left(w) - красная

3-й

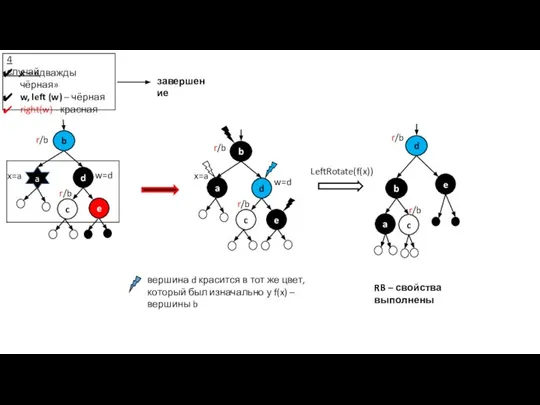
LeftRotate(f(x))

r/b

a

r/b

завершение

a

b

c

r/b

RB – свойства выполнены

вершина d красится в тот же цвет,
который был

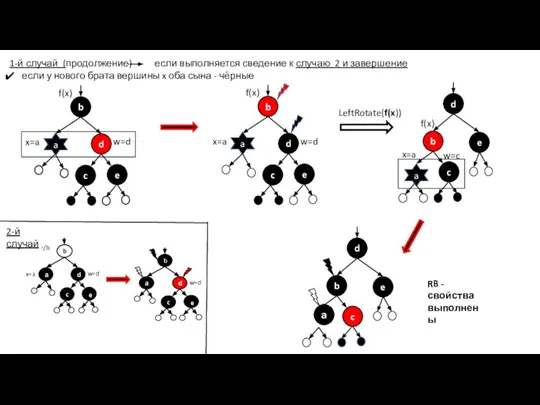
RB -свойства выполнены

1-й случай (продолжение) если выполняется сведение к случаю 2

Случаи 1, 3 и 4. Выполняются за время O(1) (выполняется самое

Удаление

ФПМИ БГУ

поиск удаляемой вершины – O(log n)
непосредственное удаление вершины – O(log

Сравнение

2. Добавление элемента

АВЛ
поиск отца для добавляемой вершины – O(h)
непосредственное добавление вершины

http://nathanbelue.blogspot.com/2012/05/red-black-versus-avl.html

Тесты показывают, что АВЛ-деревья быстрее красно-чёрных во всех операциях

https://radius-server.livejournal.com/598.html

Структуры данных и алгоритмы: теория и практика: учеб. пособие / В.М.