ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Если функция f(x)
непрерывна на отрезке

то определенный интеграл
от этой

если подынтегральная функция
на отрезке задана

Метод прямоугольников

основан на непосредственном
определении интеграла:

где

- интегральная сумма, соответствующая

Вычисление определенного
интеграла

геометрически сводится
к вычислению площади
криволинейной трапеции,

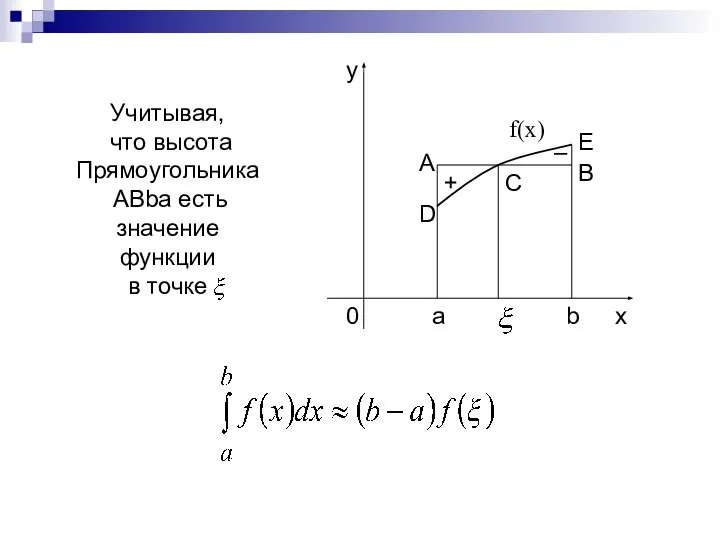
Учитывая,
что высота
Прямоугольника
ABba есть
значение
функции
в точке

f(x)

–

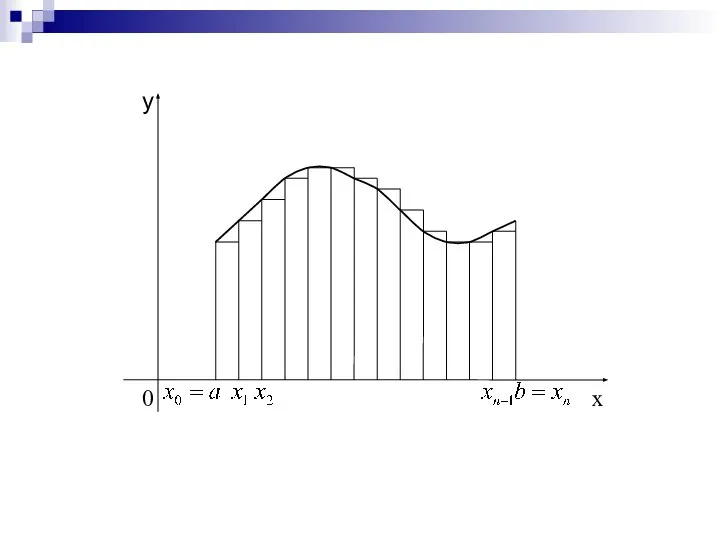
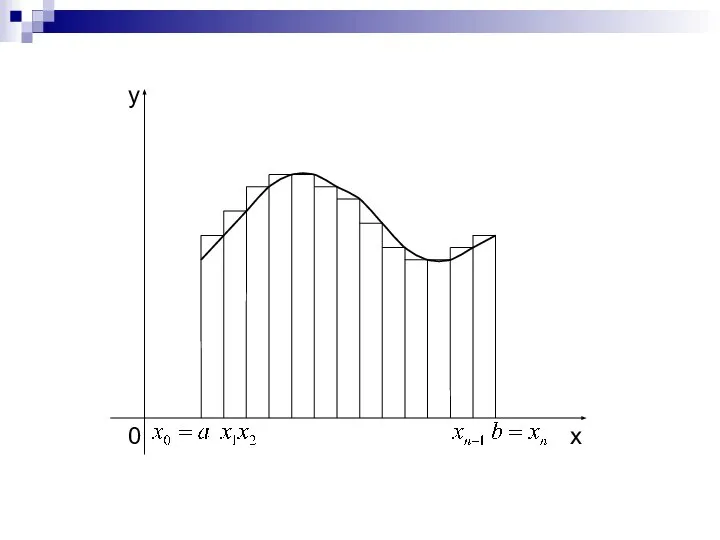
Для увеличения точности
численного интегрирования
можно отрезок

разбить на несколько

Практически удобно делить
отрезок

на равные части, а точки

 (i = 0, 1, …, n – 1)

Если точку

совместить с левым концом
отрезка

то приближенное значение

Если же в качестве точки

выбрать правый конец отрезка

то

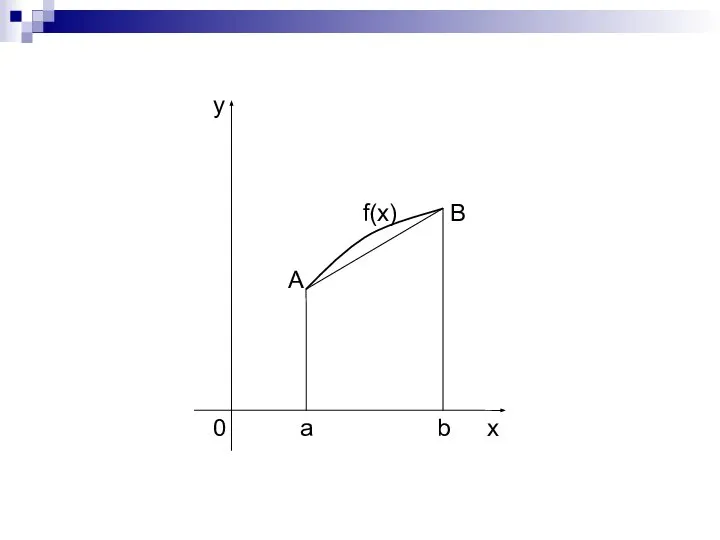
Метод трапеций

Заменим на отрезке

дугу AB графика
подынтегральной функции y = f(x)

Если отрезок

разделить на несколько
частей и применить
формулу трапеции

Для простоты вычислений
удобно разделить отрезок

на равные части,
в

А на всем отрезке

соответственно

Эта формула называется
общей формулой трапеции.

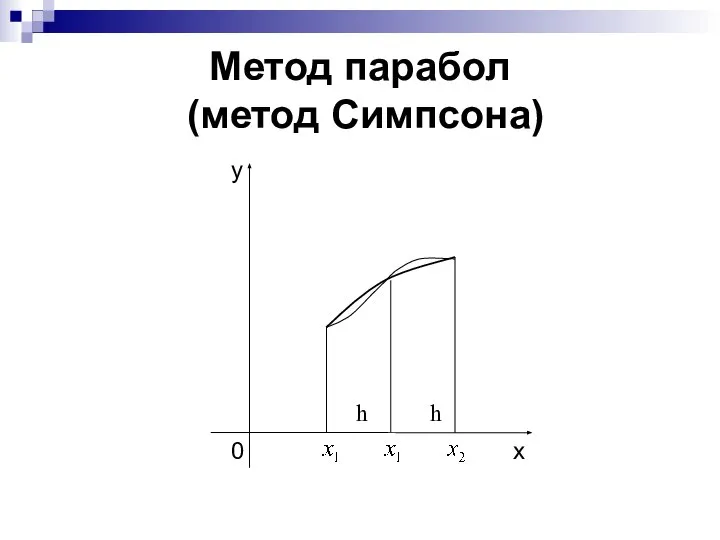
Метод парабол (метод Симпсона)

h

h

функцию y = f(x) на отрезке

заменяем квадратичной функцией,
принимающей в узлах

Тогда

Это соотношение
называется формулой Симпсона.

Для увеличения точности
вычислений отрезок

разбивают на n пар участков