1.Способ неопределенных коэффициентов для нахождения частного решения неопределенного линейного уравнения.

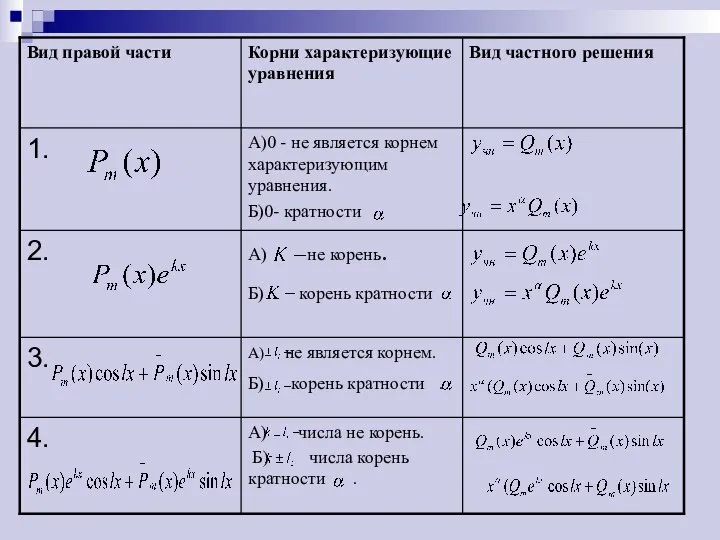
Этот способ применим для правой части специального вида, которая содержит показательные

Если правая часть имеет вид , то частное решение примет следующий вид

2.Метод вариации произвольной постоянной решения линейных неоднородных дифференциальных уравнений с постоянными

Окончательно, для нахождения неизвестных функций , мы получим систему уравнений с

4. Линейные уравнения с переменными коэффициентами.

Уравнения Бесселя. Функция Бесселя.

Задача: Вертикально стоящий и изгибающийся под действием своего

Определение

Функции, удовлетворяющие уравнению Бесселя, называются функциями Бесселя.

функцию, являющуюся решением дифференциального уравнения называют бесселевой функцией первого рода с

Чтобы получить окончательное выражение для , вводят специальную функцию- Гамма функцию

Для натурального получаем
; ,
и так далее,

Второе частное решение зависит от и, окончательно

Иногда вместо берут линейную комбинацию, содержащую , , т.е
, тогда

Функция Бесселя и тригонометрические функции связаны тесно: при определении они ведут

Уравнение Лагранжа с переменными коэффициентами
натуральные решения- многочлены, которые выражаются формулой

5. Уравнение Эйлера.

Определение1.

Уравнение вида
где , называется уравнением Эйлера.

Теорема1:

Уравнение Эйлера приводится к линейному уравнению с постоянными коэффициентами заменой

Определение2

Однородное уравнение Эйлера имеет вид

Глава3. Системы дифференциальных уравнений.

1.Нормальные системы дифференциальных уравнений.

Дано:
пусть

Таким образом, из уравнения ого порядка мы получили систему дифференциальных уравнений

Полученная система представляет собой частный случай системы

Определение1

Такая система называется нормальной системой дифференциальных уравнений.

Определение2.

Решением системы называется совокупность функций
, удовлетворяющих всем уравнением системы.

Определение3.

Частным решением системы называется решение, удовлетворяющее начальным условиям.

Замечание.

Для нормальной системы дифференциальных уравнений может быть доказана теорема существования

Теорема:

Нормальная система дифференциальных уравнений первого порядка эквивалентна одному дифференциальному уравнению

Методы решения:

1). Переходят к уравнению ого порядка
2). Метод интегрирования комбинаций,

2. Линейные системы с постоянными коэффициентами.

Определение

Нормальная система дифференциальных уравнений называется линейной, если функции
линейны