Содержание
- 2. Логика – это наука о формах и способах мышления Джордж Буль (1815-1864) основоположник математической логики
- 3. Формы мышления Основные формы мышления: Понятие Высказывание (суждение) Утверждение, рассуждение Умозаключение Логич выражение
- 4. 1. Понятие Понятие – это форма мышления, отражающая основные, наиболее существенные свойства объекта , отличающие его
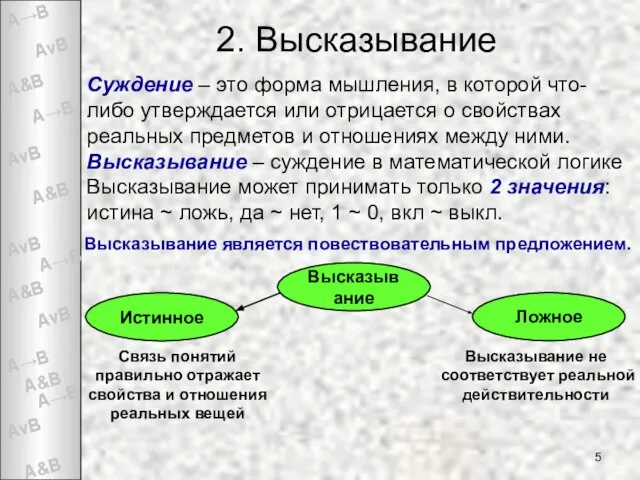
- 5. 2. Высказывание Суждение – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных
- 6. Какие из предложений являются высказыванием? Число 6 четное Посмотри на доску Все роботы машины Кто отсутствует
- 7. Простые и сложные высказывания Обоснование истинности или ложности простых высказываний решается вне алгебры логики, устанавливается законами
- 8. 3. Утверждение Утверждение – суждение, которое требуется доказать или опровергнуть Рассуждение – цепочка высказываний или утверждений,
- 9. 4. Умозаключение Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок)
- 10. 5. Логическое выражение утверждение, состоящее из постоянных и обязательно переменных величин (объектов). В зависимости от значений
- 11. Алгебра высказываний Алгебра высказываний служит для определения истинности или ложности составных высказываний (смысловое содержание простых высказываний
- 12. Высказывания могут быть простыми и сложными. Опр.: Высказывание является простым, если никакая его часть сама по
- 13. Опр.: сложные высказывания (выражения) состоят из простых (или сложных) высказываний, объединенных логическими операциями. Основные логические операции:
- 14. Логические операции 2.1. Логическое умножение (конъюнкция) 2.2. Логическое сложение (дизъюнкция) 2.3. Логическое отрицание (инверсия) 2.4. Логическое
- 15. 1. Логическое умножение (конъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «и». Составное
- 16. 2. Логическое сложение (дизъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «или». Составное
- 17. 3. Логическое отрицание (инверсия) Присоединение частицы «не» к высказыванию. Инверсия делает истинное высказывание ложным и, наоборот.
- 18. 4. Логическое следование (импликация) Соответствует обороту Если…, то… (из А следует В) Обозначение →, ⇨ В
- 19. 5. Логическое равенство (эквивалентность) Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «…
- 20. 6. Логическое сложение по модулю (исключающее ИЛИ) Исключающее ИЛИ образуется соединением двух высказываний в одно с
- 21. Логические выражения Логическое выражение – формула, в которую входят логические переменные и знаки логических операций. Пример:
- 22. Найдите значения логических выражений
- 23. Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных
- 24. Построение таблицы истинности Подсчитать кол-во переменных в выражении =n. Число строк в таблице = 2n +
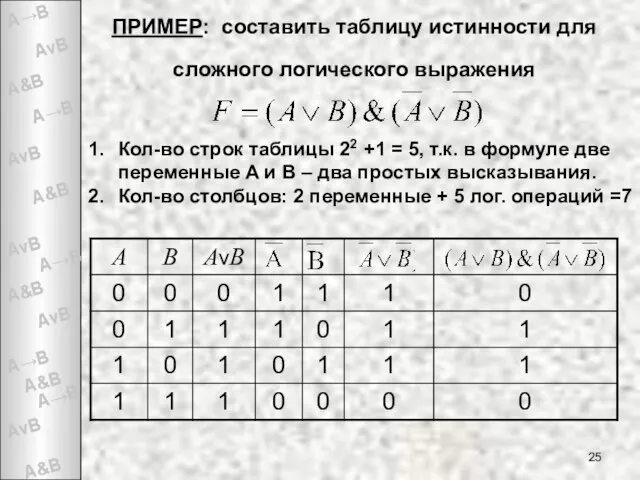
- 25. ПРИМЕР: составить таблицу истинности для сложного логического выражения Кол-во строк таблицы 22 +1 = 5, т.к.
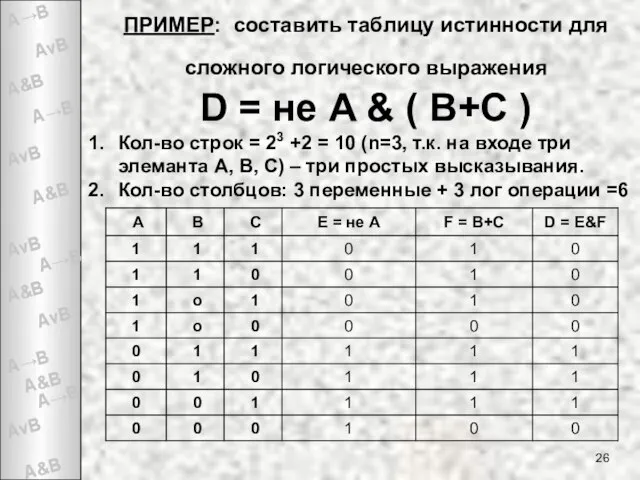
- 26. ПРИМЕР: составить таблицу истинности для сложного логического выражения D = не A & ( B+C )
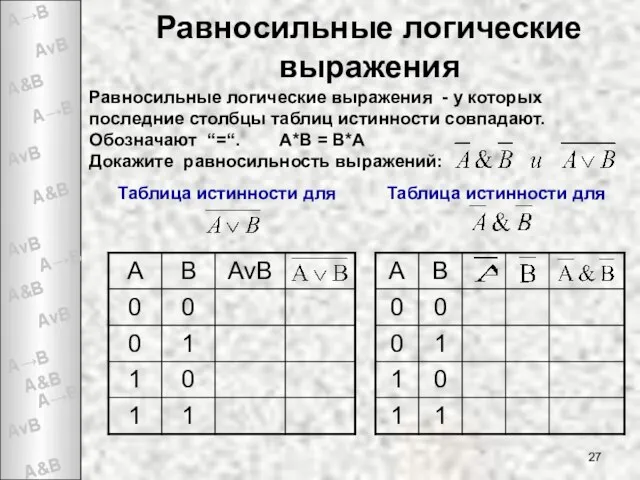
- 27. Равносильные логические выражения Равносильные логические выражения - у которых последние столбцы таблиц истинности совпадают. Обозначают “=“.
- 28. Докажите равносильность выражений: А+В+С=В+С+А АВС=ВСА А⬄В=¬А⬄¬В (А+В)С=АС+ВС АВ+С=(А+С)(В+С) ¬(А+В)=¬А¬В ¬(АВ)=¬А+¬В АВ+¬АВ=В (А+В)(¬А+В)=В ¬А(А+В)=¬АВ А+¬АВ=А+В
- 29. Выражение называется тождественно ложным (истинным), если оно принимает значение 0 (1) на всех наборах, входящих в
- 30. Основные понятия ЛОГИКИ ПРЕДИКАТОВ В алгебре логики высказывания рассматриваются как единый объект с точки зрения истинности
- 31. Определение. Одноместным предикатом P(x) называется произвольная функция переменной x, определенная на множестве М и принимающая значение
- 32. Используя функциональную форму записи для предикатов, можно сказать, что предикатом Р(х1, х2, …, хn) называется функция
- 33. Таким образом, n-местный предикат, − это двузначная функция от n аргументов, определенная на произвольном множестве М,
- 34. Возможность описывать с помощью предикатов не только функции, но и отношения, определяется следующим: а) если а1,
- 35. Таким образом, в общем случае предикат Р – двоичная переменная, то есть переменное высказывание, истинность которого
- 36. Примеры. 1.Рассмотрим утверждение «x – целое число». Введем предикат I, обозначающий отношение «быть целым числом», тогда
- 37. 3. Элементы хi множества М – города. Предикат Р(х) устанавливается таким образом: «х – это столица
- 38. Пример (для предикатов определенных в предыдущем примере). Пусть в обоих случаях предикаты определены на множестве R
- 39. Предикат называется тождественно истинным, если на любом наборе аргументов он принимает значение 1. Предикат называется тождественно
- 40. Квантор всеобщности (∀). Пусть P(x) это предикат, определенный на множестве М. Тогда под выражением − понимается
- 42. Скачать презентацию



































 Симметрия. Центральная и осевая симметрии
Симметрия. Центральная и осевая симметрии Составление практических заданий на применение формул сокращённого умножения
Составление практических заданий на применение формул сокращённого умножения Теория вероятностей
Теория вероятностей Решение задач в два действия
Решение задач в два действия Числа 1 – 5 закрепление
Числа 1 – 5 закрепление Системы двух линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя переменными Трапеция және оның қасиеттері
Трапеция және оның қасиеттері Параметр на ЕГЭ
Параметр на ЕГЭ Вычисление значений функции по формуле
Вычисление значений функции по формуле Практика по темам «Последовательность» и «Арифметическая прогрессия»
Практика по темам «Последовательность» и «Арифметическая прогрессия» Геометрические построения
Геометрические построения Лекция 12. Интегрирование рациональных дробей, иррациональных дробей, тригонометрических функций
Лекция 12. Интегрирование рациональных дробей, иррациональных дробей, тригонометрических функций Тіктөртбұрыш пен шаршының ауданы
Тіктөртбұрыш пен шаршының ауданы Урок обобщающего повторения: Степерь с рациональным показателем и ее свойства
Урок обобщающего повторения: Степерь с рациональным показателем и ее свойства Презентация по математике "ТАБЛИЦА УМНОЖЕНИЯ НА 2 И 3" - скачать бесплатно
Презентация по математике "ТАБЛИЦА УМНОЖЕНИЯ НА 2 И 3" - скачать бесплатно ДРОБИ. Дроби всякие нужны, Дроби всякие важны. Дробь учи, тогда сверкнёт удача. Если дроби будешь знать , Точно смысл и
ДРОБИ. Дроби всякие нужны, Дроби всякие важны. Дробь учи, тогда сверкнёт удача. Если дроби будешь знать , Точно смысл и Построение графика функций
Построение графика функций Тела вращения. Площади поверхности и объёмы
Тела вращения. Площади поверхности и объёмы Преобразование фигур в пространстве
Преобразование фигур в пространстве Сумма углов многоугольника
Сумма углов многоугольника «В здоровом теле- здоровый ум»
«В здоровом теле- здоровый ум»  Предельные теоремы теории вероятногстей
Предельные теоремы теории вероятногстей Степень с натуральным показателем
Степень с натуральным показателем Урок по теме «Координатная плоскость»(6 класс) МОБУ «Новочеркасская СОШ» Булдакова Л.П.
Урок по теме «Координатная плоскость»(6 класс) МОБУ «Новочеркасская СОШ» Булдакова Л.П.  Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Второй и третий признаки равенства треугольников
Второй и третий признаки равенства треугольников Равносильность неравенств
Равносильность неравенств Применение разноуровневого обучения на уроках математики Путинцева Любовь Алексеевна
Применение разноуровневого обучения на уроках математики Путинцева Любовь Алексеевна