Содержание
- 2. Интегрирование простейших рациональных дробей Класс рациональных функций можно представить в виде дроби где P(x) и Q(x)
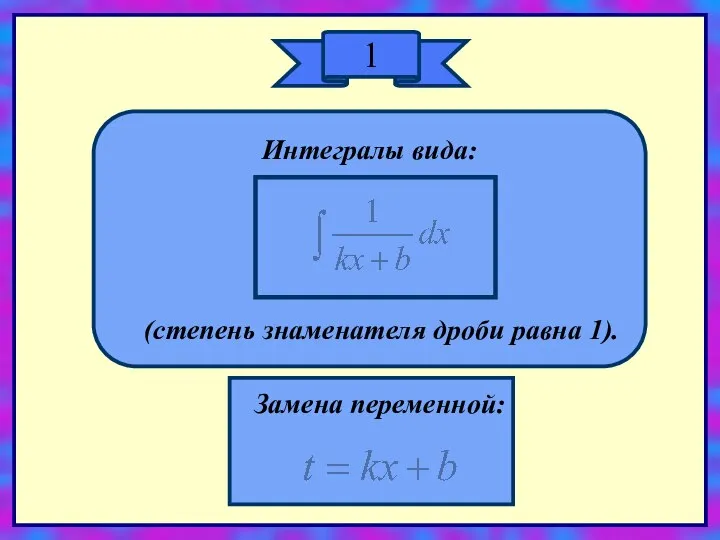
- 3. 1 Интегралы вида: (степень знаменателя дроби равна 1). Замена переменной:
- 4. Пример. Вычислить интеграл:
- 5. Решение:
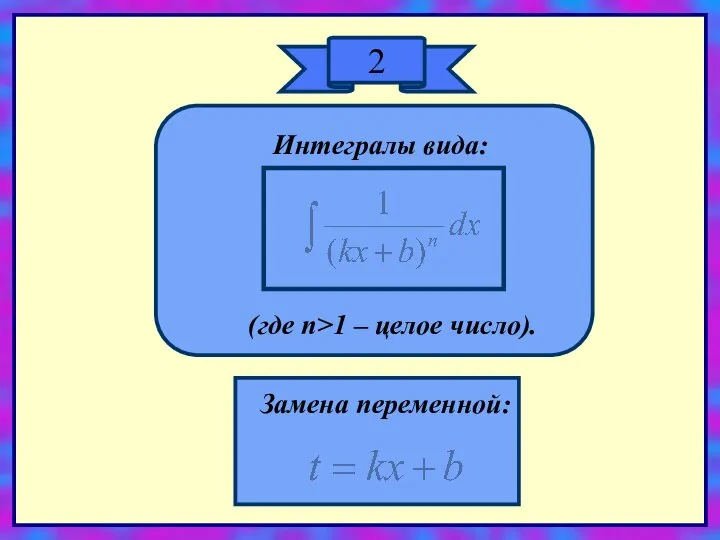
- 6. 2 Интегралы вида: (где n>1 – целое число). Замена переменной:
- 7. Пример. Вычислить интеграл:
- 8. Решение:
- 9. 3 Интегралы вида:
- 10. В знаменателе дроби выделяется полный квадрат и делается линейная замена переменной, так что интеграл сводится к
- 11. Второй интеграл при сводится к табличному: а при сводится к табличному:
- 12. Примеры. Вычислить интеграл: 1
- 13. Решение:
- 15. Вычислить интеграл: 2
- 16. Решение:
- 18. 4 Метод неопределенных коэффициентов Рассмотренный выше способ вычисления интегралов от рациональных дробей не обобщается на случай,
- 19. Этот метод связан с представлением подынтегральной дроби в виде суммы простых дробей. Для этого знаменатель дроби
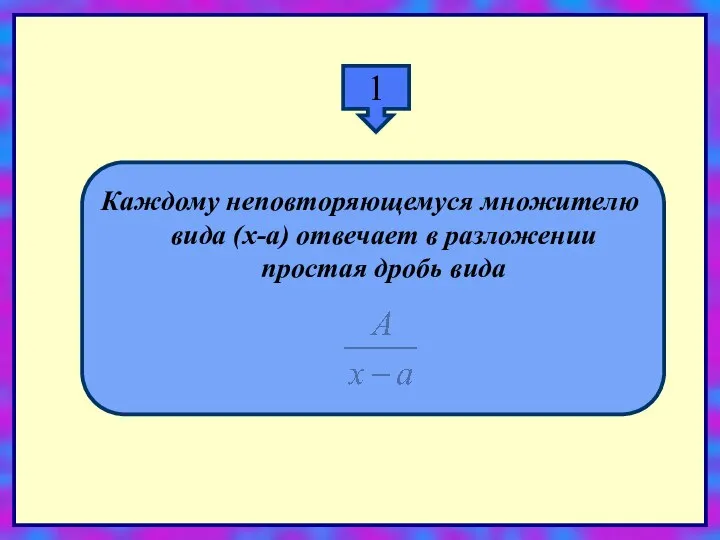
- 20. 1 Каждому неповторяющемуся множителю вида (x-a) отвечает в разложении простая дробь вида
- 21. 2 Каждому множителю вида (x-a)n отвечает в разложении сумма n простых дробей вида
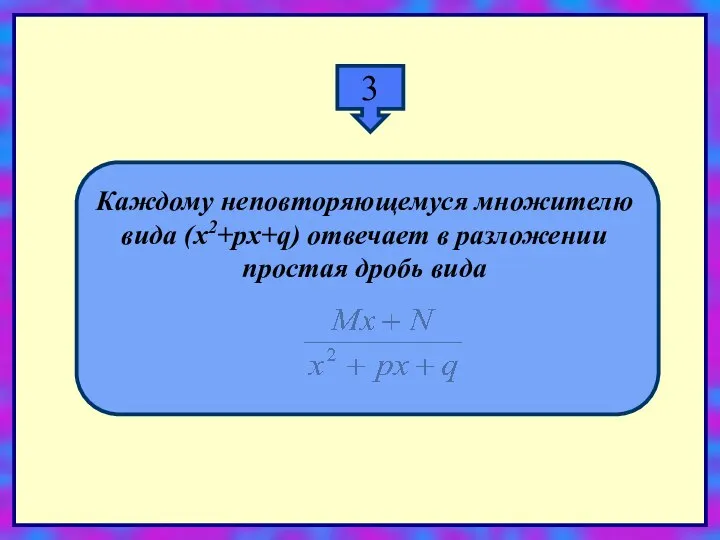
- 22. 3 Каждому неповторяющемуся множителю вида (x2+px+q) отвечает в разложении простая дробь вида
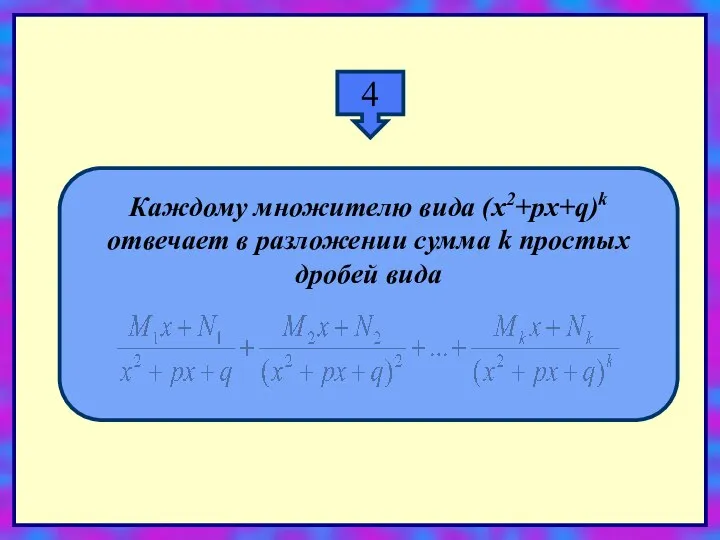
- 23. 4 Каждому множителю вида (x2+px+q)k отвечает в разложении сумма k простых дробей вида
- 24. Пример. Вычислить интеграл:
- 25. Решение:
- 26. При При При
- 28. Скачать презентацию













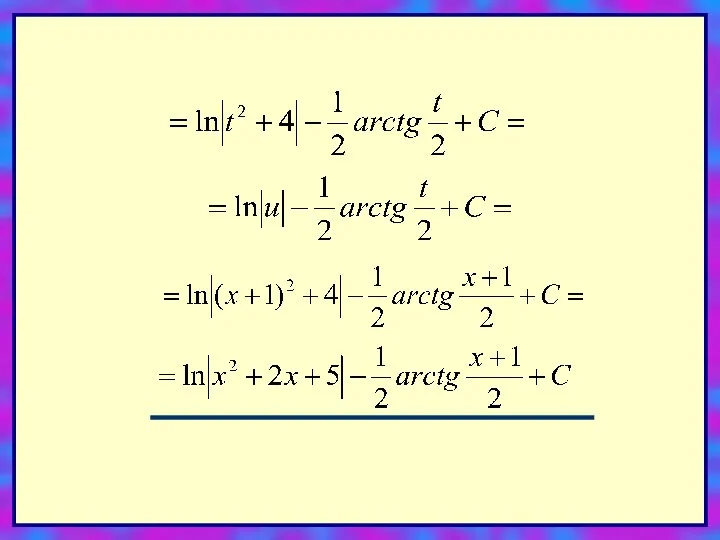






 Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей Алгоритм сложения трехзначных чисел с двумя переходами через разряд
Алгоритм сложения трехзначных чисел с двумя переходами через разряд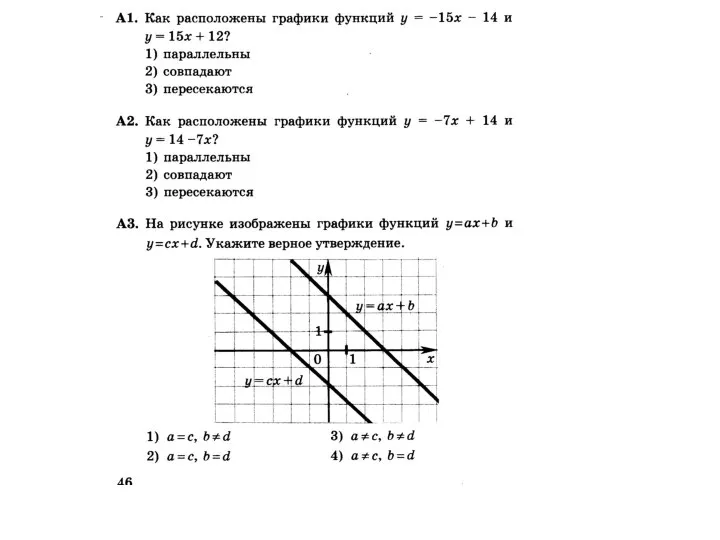 Линейная функция. График линейной функции
Линейная функция. График линейной функции Умножение рациональных чисел
Умножение рациональных чисел Что такое число π
Что такое число π Вектор ұғымы
Вектор ұғымы Презентация по математике "Вычисление площадей с помощью интегралов" - скачать
Презентация по математике "Вычисление площадей с помощью интегралов" - скачать  Преобразование графика функции
Преобразование графика функции Круги Эйлера
Круги Эйлера Точки на прямой. Вопросы, упражнения
Точки на прямой. Вопросы, упражнения Итоговый тест по математике. 5 класс
Итоговый тест по математике. 5 класс Масса тела и ее измерение
Масса тела и ее измерение Что лишнее?
Что лишнее? Случайные процессы (лекция 13). Закон распределения и основные характеристики случайных процессов
Случайные процессы (лекция 13). Закон распределения и основные характеристики случайных процессов Системы координат, применяемые в механике полета
Системы координат, применяемые в механике полета Деление одночлена на одночлен Тема урока
Деление одночлена на одночлен Тема урока Основы функционального анализа. Глава 2. Линейные нормированные пространства
Основы функционального анализа. Глава 2. Линейные нормированные пространства «Логарифмическая функция, ее свойства и график.» Подготовил учитель математики СШ №12 Пышкин К.А.
«Логарифмическая функция, ее свойства и график.» Подготовил учитель математики СШ №12 Пышкин К.А.  Абсолютная величина числа
Абсолютная величина числа Деление положительных десятичных дробей. Презентация Кружилиной Арины, ученицы 6 «Б» класса_
Деление положительных десятичных дробей. Презентация Кружилиной Арины, ученицы 6 «Б» класса_ Интернет ресурсы при подготовке к ГИА по математике
Интернет ресурсы при подготовке к ГИА по математике 17 формул, изменивших мир
17 формул, изменивших мир Значение переменной после выполнения алгоритма
Значение переменной после выполнения алгоритма Презентация на тему натуральные числа и шкалы 5 класс.
Презентация на тему натуральные числа и шкалы 5 класс.  Множества. Операции над множествами. Примеры множеств
Множества. Операции над множествами. Примеры множеств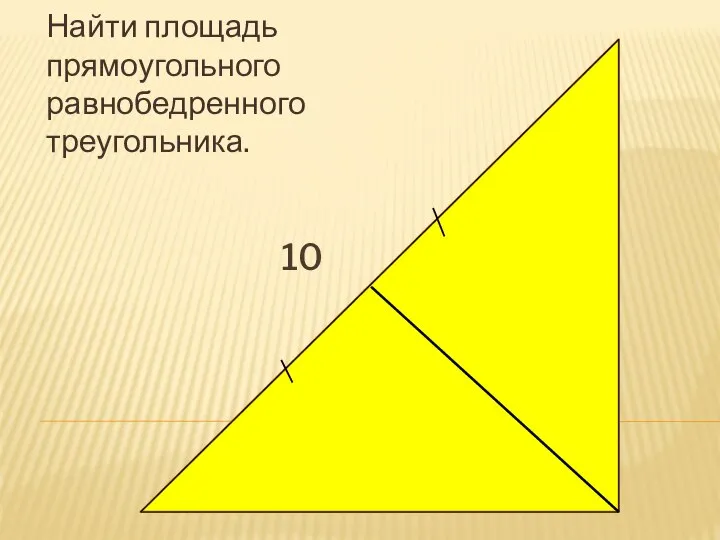 Решение задач. Площадь прямоугольного равнобедренного треугольника
Решение задач. Площадь прямоугольного равнобедренного треугольника Свойства элементарных функций
Свойства элементарных функций Преобразование графиков функций. Часть 1
Преобразование графиков функций. Часть 1