Содержание
- 2. Неравенство Чебышева. Неравенство Маркова (или лемма Чебышева) Если случайная величина Х принимает только неотрицательные значения и
- 3. Теорема Чебышева. Закон больших чисел (ЗБЧ). Введем понятие сходимости по вероятности:
- 4. Формулировка ЗБЧ в форме Чебышева П.Л. (теорема Чебышева): Если дисперсии n независимых случайных величин Х1 ,
- 5. Следствия из теоремы Чебышева: Первое следствие: Теорема Хинчина Если независимые случайные величины Х1 , Х2,…, Хn
- 6. Второе следствие: Теорема Бернулли Пусть проводится n независимых испытаний, в каждом из которых событие А может
- 7. Третье следствие: ЗБЧ может быть распространен и на зависимые случайные величины ( это обобщение принадлежит Маркову
- 8. Смысл и формулировка центральной предельной теоремы (ЦПТ). Интегральная теорема Муавра-Лапласа как следствие ЦПТ. Эта теорема утверждает,
- 9. Упрощенная математическая формулировка ЦПТ: Если X1 , X2 ,…, Xn – независимые случайные величины, для каждой
- 10. Многомерная случайная величина и закон ее распределения. Пусть имеется система случайных величин (СВ), причем эта система
- 11. Эта функция выражает вероятность совместного выполнения неравенств в правой части этого соотношения. С целью экономии времени
- 12. Для двумерной непрерывной случайной величины (X,Y) функция совместного распределения может быть представлена в виде: Для функции
- 13. Для независимых случайных величин Х и Y независимы события {X Для непрерывных СВ из данного соотношения,
- 14. Стохастическая зависимость двух случайных величин. Ковариация и коэффициент корреляции. Если случайные величины зависимы, влияют на поведение
- 15. Рассмотрены свойства ковариации. Вывод: ковариация не улавливает сложные виды связей между X и Y. Ковариация отслеживает
- 16. Определение. Случайные величины называются некоррелированными, если их коэффициент корреляции равен нулю. Случайные величины называются коррелированными, если
- 17. Для вычисления коэффициента корреляции между двумя количественными признаками на практике используется линейный коэффициент корреляции Пирсона:
- 18. Введем коэффициент корреляции для изучения тесноты связи между порядковыми случайными величинами. Если n объектов совокупности пронумеровать
- 19. В случае совпадения рангов при вычислении коэффициента ранговой корреляции следует брать среднее арифметическое рангов, приходящихся на
- 21. Скачать презентацию


















 Построение графиков функций, содержащих переменную под знаком модуля
Построение графиков функций, содержащих переменную под знаком модуля Теория кривых. Репер Френе
Теория кривых. Репер Френе График функции
График функции Математический диктант по теме: «Дроби». 6 класс
Математический диктант по теме: «Дроби». 6 класс Определение степени с целым отрицательным показателем
Определение степени с целым отрицательным показателем Графические методы исследования
Графические методы исследования Оригами и геометрия. Аксиомы оригаметрии
Оригами и геометрия. Аксиомы оригаметрии Тест по теме: "Объем наклонной призмы, пирамиды и конуса". Вариант 2
Тест по теме: "Объем наклонной призмы, пирамиды и конуса". Вариант 2 Путешествие в страну дробных чисел. 6 класс
Путешествие в страну дробных чисел. 6 класс Принципы системного подхода к формированию систем статистических показателей
Принципы системного подхода к формированию систем статистических показателей Мир десятичных дробей
Мир десятичных дробей Построение графика квадратичной функции сдвигом
Построение графика квадратичной функции сдвигом Построение сечения плоскостью
Построение сечения плоскостью Элементы теории игр
Элементы теории игр Внеклассное занятие. Математический брейн-ринг
Внеклассное занятие. Математический брейн-ринг Пифагор Самосский
Пифагор Самосский Распределительный закон умножения
Распределительный закон умножения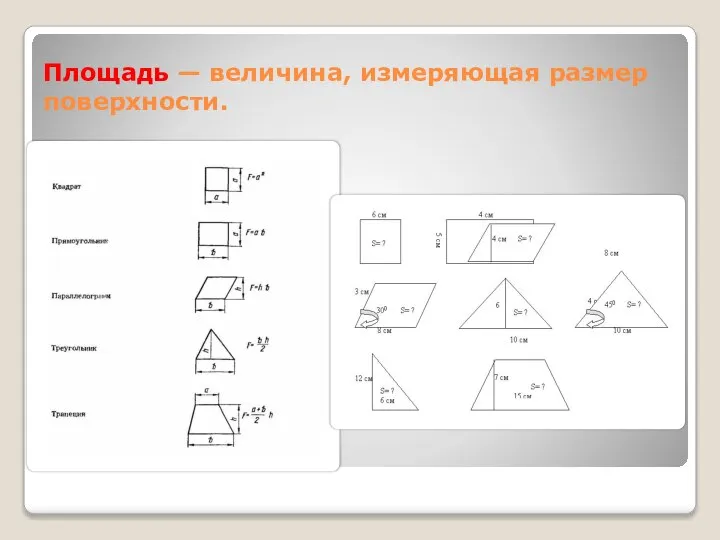 Площадь — величина, измеряющая размер поверхности.
Площадь — величина, измеряющая размер поверхности. Ф.И. Класс Тема урока
Ф.И. Класс Тема урока Исследование алфавита знаков для кодирования информации
Исследование алфавита знаков для кодирования информации Медицинская статистика. Значение, методы
Медицинская статистика. Значение, методы Комбинаторика. Формулы сложения и произведения. Примеры
Комбинаторика. Формулы сложения и произведения. Примеры Задачи В4 (на умение использовать приобретенные знания, умения и навыки в практической деятельности и повседневной жизни)
Задачи В4 (на умение использовать приобретенные знания, умения и навыки в практической деятельности и повседневной жизни) Задачи на деление
Задачи на деление Теорема синусов
Теорема синусов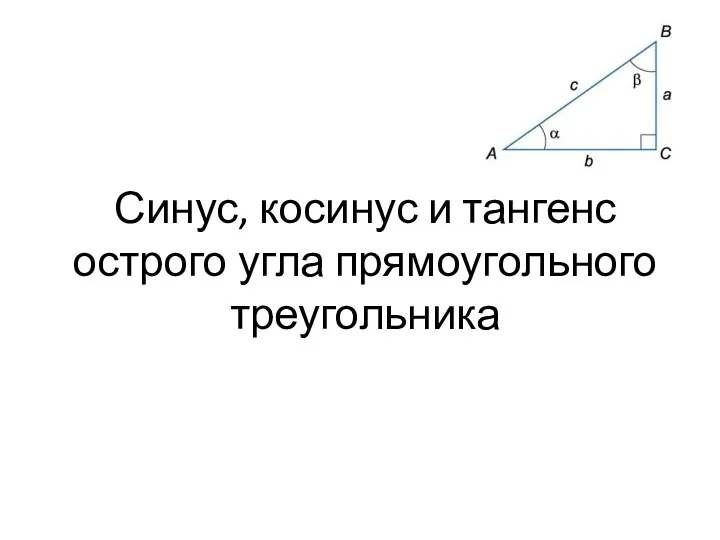 Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Технология личностно-ориентированного обучения на уроках математики путем индивидуализации и дифференциации обучения
Технология личностно-ориентированного обучения на уроках математики путем индивидуализации и дифференциации обучения Незнайка. Урок математики
Незнайка. Урок математики