Алгебра: Матрицы. Действия с матрицами. Определитель. Его вычисление и основные свойства

Матрицы.

Определение: Матрица размерности mxn – это таблица чисел расположенных в m

Матрицы.

3

Нулевая матрица

Побочная диагональ

Главная диагональ

Единичная матрица

Матрица столбец

Матрица строка

Действия над матрицами.

Сложение матриц:

4

Вычитание матриц:

Умножение матрицы на число:

Действия над матрицами

Умножение матриц:

5

Пример умножения матриц.

6

Действия над матрицами.

Операции сложения и умножения матриц обладают следующими свойствами:
Сложения:
А+В=В+А (переместительный

Определитель матрицы.
Каждой квадратной матрице ставится в соответствие число, называемое определителем матрицы.
Обозначается:

Вычисление определителя.

Для матрицы размера 2х2, определитель вычисляется по следующей формуле:

9

Для вычисления

Вычисление определителя.

Будем называть минором (Mkl) определитель матрицы полученной из исходной после

Вычисление определителя.

Алгебраическим дополнением элемента матрицы с индексами k, l называется число

Вычисление определителя.

Определитель матрицы размера более чем 3х3, вычисляется путем разложения этой

Вычисление определителя.

Для вычисления определителя матрицы 3х3 можно использовать следующую формулу:

13

Пример вычисление определителя.

14

Пример вычисление определителя.

15

Пример вычисление определителя.

16

Свойства определителей.

17

Свойство 1. При перестановке двух строк (или столбцов) определитель меняет

Свойства определителей.

18

Свойство 5. Если все элементы некоторой строки (столбца) нули, то

Система линейных алгебраических уравнений (СЛАУ)

Система вида:
где матрица системы,
- вектор неизвестных,

Система линейных алгебраических уравнений (СЛАУ)

Если обозначим:

20

То нашу систему можно записать в

Система линейных алгебраических уравнений (СЛАУ)

21

Обратная матрица – это такая матрица при

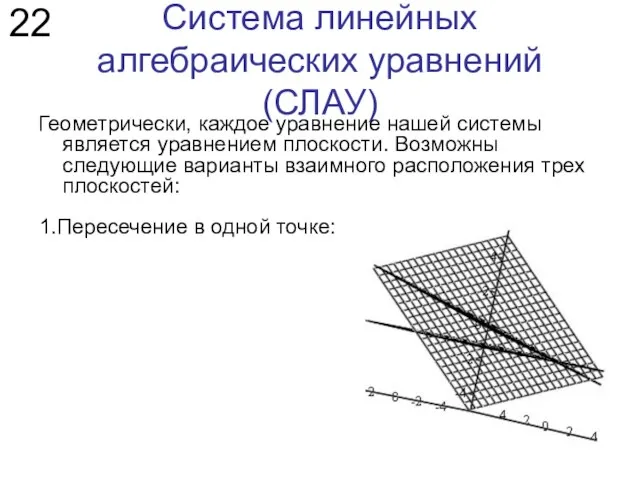
Система линейных алгебраических уравнений (СЛАУ)

Геометрически, каждое уравнение нашей системы является уравнением

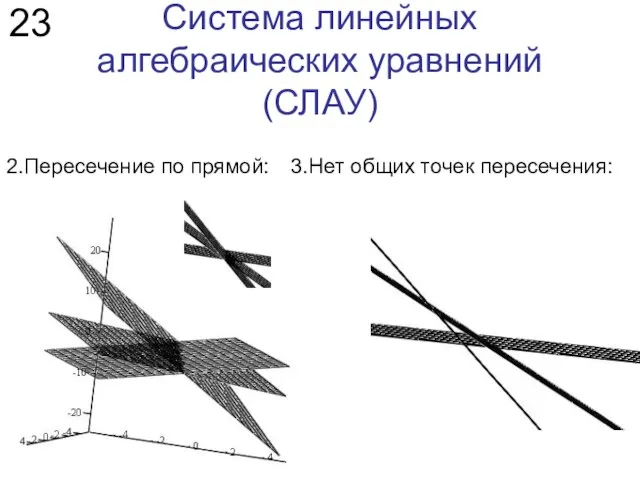
Система линейных алгебраических уравнений (СЛАУ)

23

2.Пересечение по прямой:

3.Нет общих точек пересечения:

Система линейных алгебраических уравнений (СЛАУ)

В первом случае определитель нашей системы НЕ

Метод Крамера.

Данный метод сводиться к нахождению четырех определителей:

25

Метод Крамера.

В результате получим решение СЛАУ:

26

Метод Крамера. Пример.

Решить систему уравнений:

27

Метод Крамера. Пример.

Вычислим определитель системы:

28

Метод Крамера. Пример.

29

Метод Крамера. Пример.

30

Метод Крамера. Пример.

31

Метод Крамера. Пример.

В результате мы получили: D=5, D1=0, D2=0, D3=10.

32

Метод Крамера. Пример.

33

Решение СЛАУ методом обратной матрицы.

34

Решение СЛАУ методом обратной матрицы.

35

Решение СЛАУ методом обратной матрицы.

36

Решение СЛАУ методом обратной матрицы.

37

Метод Гаусса

Расширенной матрицей системы

38

будем называть матрицу вида

Метод Гаусса

Ранг матрицы – это размер наибольшего ненулевого минора этой матрицы.
Ранг

Метод Гаусса

Для того, чтобы СЛАУ была совместна ранг матрицы системы должен

Метод Гаусса

Сам метод Гаусса состоит в том, чтобы преобразованием строк получить

Метод Гаусса

42

Метод Гаусса

43

Вычитаем из 3 строки первую строку
Добавим к 3 строке вторую

Метод Гаусса

44

Теперь из расширенной матрицы запишем получившуюся систему:

Метод Гаусса

Осталось только решить нашу систему. Из последнего уравнения получаем z=2,

Метод Гаусса

Исследовать СЛАУ на совместность:

46

Запишем расширенную матрицу системы:

Метод Гаусса

47

Вычитаем из 2 строки первую
Вычитаем из 3 строки первую умноженную

Метод Гаусса

Заметим, что наибольший ненулевой минор имеет размерность 2, а количество

Метод Гаусса

Исследовать СЛАУ на совместность:

49

Запишем расширенную матрицу системы:

Метод Гаусса

50

Вычитаем из 2 строки первую
Вычитаем из 3 строки первую умноженную