Содержание
- 2. Содержание: Полиномиальный коэффициент Формула полинома Биномиальные коэффициенты Бином Ньютона Выводы Тема: Бином Ньютона. Полиномиальная формула Цель
- 3. Литература Глускин Л.М., Шор Л.А., Шварц В.Я. Задачи и алгоритмы комбинаторики, и теории графов. Донецк, ДПИ,
- 4. Базовые понятия: Множество Число Целое число Натуральное число Рациональное число Иррациональное число Степень Факториал Термины Ключевые
- 5. Полиномиальный коэффициент Def: определенная для всех натуральных n и всех наборов неотрицательных целых чисел k1,k2,…,km, для
- 6. Формула полинома Def: для любых действительных чисел а1,а2, …, аm не равных нулю и любого натурального
- 7. Пример Написать разложение полинома третьей степени Задание: определить полиномиальные коэффициенты в данном разложении
- 8. Биномиальные коэффициенты Обозначение: или Чтение: – «С из n по k»; – «n над k» Def:
- 9. Треугольник Паскаля Значения биномиальных коэффициентов могут быть последовательно определены из треугольника Паскаля:
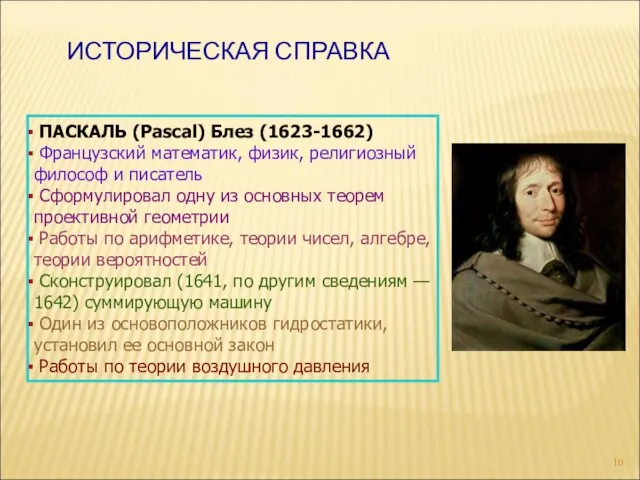
- 10. ИСТОРИЧЕСКАЯ СПРАВКА ПАСКАЛЬ (Pascal) Блез (1623-1662) Французский математик, физик, религиозный философ и писатель Сформулировал одну из
- 11. Свойства биномиальных коэффициентов Симметрия: , Каждый коэффициент образуется путем сложения двух стоящих над ним (справа и
- 12. Биномиальные коэффициенты для рациональных значений Область определения биномиальных коэффициентов можно расширить, а именно: Def: функция определенная
- 13. Примеры
- 14. Формула бинома Ньютона Биномиальные коэффициенты формулы бинома Ньютона составляют в треугольнике Паскаля строку с номером n.
- 15. Историческая справка Слово «бином» (от латинского bis − дважды и греческого nomos − член) означает «двучлен»
- 17. Скачать презентацию












 История Кремля в математике и литературе
История Кремля в математике и литературе Что такое математическая модель
Что такое математическая модель Презентация по математике "Задача Пуассона" - скачать
Презентация по математике "Задача Пуассона" - скачать  Графики и диаграммы
Графики и диаграммы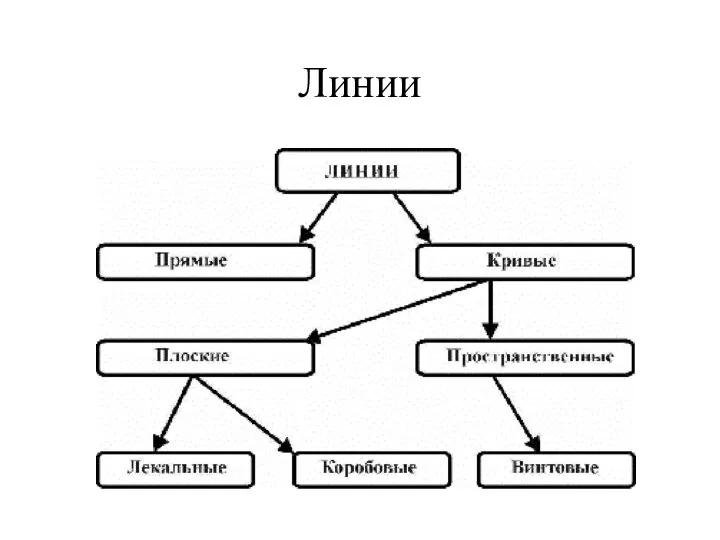 Линии. Плоские кривые. Лекальные кривые
Линии. Плоские кривые. Лекальные кривые Теорема Безу. Схема Горнера и её применения
Теорема Безу. Схема Горнера и её применения «РАВЕНСТВА И НЕРАВЕНСТВА» «РАВЕНСТВА И НЕРАВЕНСТВА» Воронцова Елена Вячеславовна ГБОУ СОШ № 156 Калининского района г. Санкт-Пе
«РАВЕНСТВА И НЕРАВЕНСТВА» «РАВЕНСТВА И НЕРАВЕНСТВА» Воронцова Елена Вячеславовна ГБОУ СОШ № 156 Калининского района г. Санкт-Пе Элементы векторной алгебры (лекция № 2)
Элементы векторной алгебры (лекция № 2) Раскрытие скобок и упрощение выражений
Раскрытие скобок и упрощение выражений Основы оптимизации перевозочного процесса. Маршрутизация перевозок массовых грузов
Основы оптимизации перевозочного процесса. Маршрутизация перевозок массовых грузов Интегрированный урок математика + история
Интегрированный урок математика + история Своя игра
Своя игра Кривые 2-го порядка: эллипс, гипербола, парабола
Кривые 2-го порядка: эллипс, гипербола, парабола Метрология. Калибровка средств измерений. (Лекция 4)
Метрология. Калибровка средств измерений. (Лекция 4) Вычитание из чисел 8 и 9. Состав 8 и 9
Вычитание из чисел 8 и 9. Состав 8 и 9 Определение производной
Определение производной Математические игры по-олимпийски
Математические игры по-олимпийски Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов) Составила учитель математики Давлятова Л.Н. П. Че
Аукцион «Продажа имения старой графини» ( математическая игра для 10-11 классов) Составила учитель математики Давлятова Л.Н. П. Че Веб – квест для учащихся 11 класса. Задачи по теме «Производная»
Веб – квест для учащихся 11 класса. Задачи по теме «Производная» Проверка статистических гипотез (лекция 9)
Проверка статистических гипотез (лекция 9)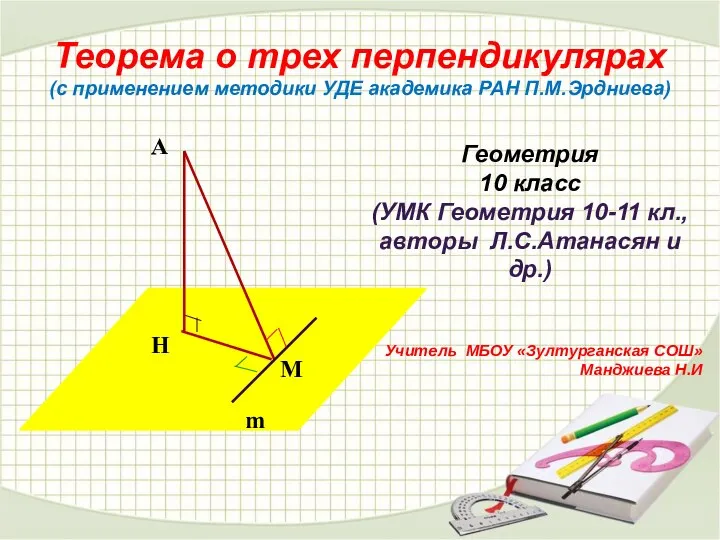 Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева)
Теорема о трех перпендикулярах (с применением методики УДЕ академика РАН П.М. Эрдниева) Правило вычисления значения алгебраической суммы двух чисел
Правило вычисления значения алгебраической суммы двух чисел Умножение многочлена на многочлен Курсовая работа Алевтины Алексеевны Рагимовой Лицей № 179 Калининского района
Умножение многочлена на многочлен Курсовая работа Алевтины Алексеевны Рагимовой Лицей № 179 Калининского района  Физминутка в картинках
Физминутка в картинках Презентация по математике "Вычитание суммы из числа и числа из суммы" - скачать бесплатно
Презентация по математике "Вычитание суммы из числа и числа из суммы" - скачать бесплатно Многоугольники
Многоугольники Презентация по математике "Построение графиков функций с использованием производной" - скачать
Презентация по математике "Построение графиков функций с использованием производной" - скачать  Решение заданий №1 по материалам открытого банка задач ЕГЭ по математике 2015 года
Решение заданий №1 по материалам открытого банка задач ЕГЭ по математике 2015 года