Содержание
- 2. При вычислении производной функции, будем иметь в виду, что один из способов найти производную - это
- 3. Таким образом, вычисляется производная в середине промежутка. По значениям f' можно таким же способом найти производную
- 4. Для производной третьего порядка можно использовать следующую формулу: Возникают естественные вопросы, откуда происходят эти формулы и
- 5. Односторонняя разность Производная функции определяется выражением: заменяем приращение на конечную величину (шаг дифференцирования): x0 f(x0) f(x0+Δx)
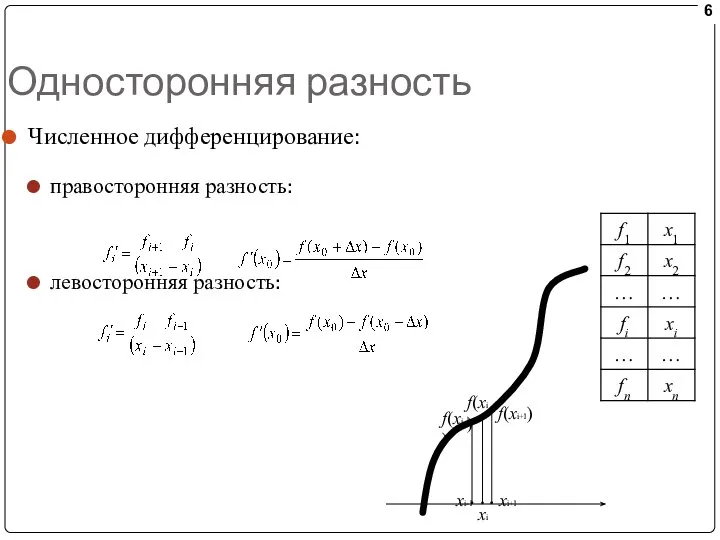
- 6. Односторонняя разность Численное дифференцирование: правосторонняя разность: левосторонняя разность: xi f(xi) f(xi+1) xi-1 xi+1 f(xi-1)
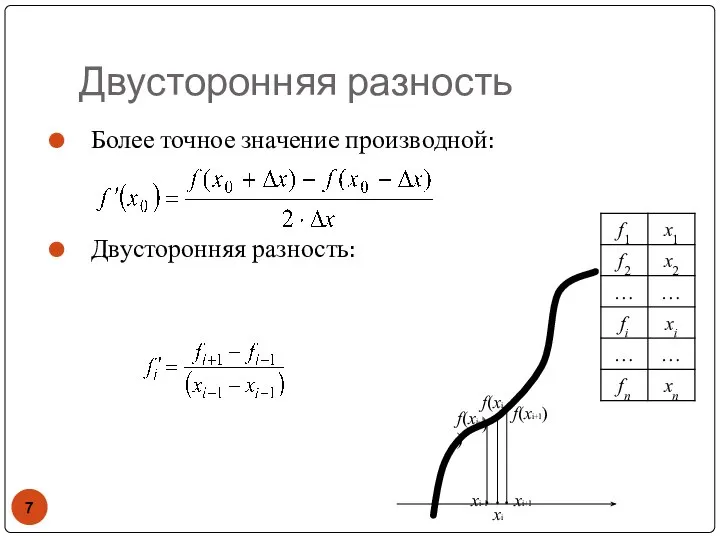
- 7. Двусторонняя разность Более точное значение производной: Двусторонняя разность: xi f(xi) f(xi+1) xi-1 xi+1 f(xi-1)
- 8. Формулы являются результатом дифференцирования интерполяционных многочленов Ньютона и других. Сущность которых состоит в том, что заданная
- 9. Оценка погрешности и точности вычисления не менее серьезный и сложный процесс, чем само приближенное вычисление. Так
- 10. На практике f (n+1)(c) оценивать непросто, поэтому при малых dx приближенно полагают: и тогда получается следующая
- 11. Мы будем пользоваться формулой (2), а впоследствии и формулой (3), в зависимости от конкретной задачи и
- 12. Частное дифференцирование функции от многих переменных Все аргументы функции становятся константами, кроме аргумента по которому проводится
- 13. Интерполяция полиномом Заданная таблица сглаживается какой-либо функцией P(x), являющейся интерполяционным полиномом, или полиномом, полученным с использованием
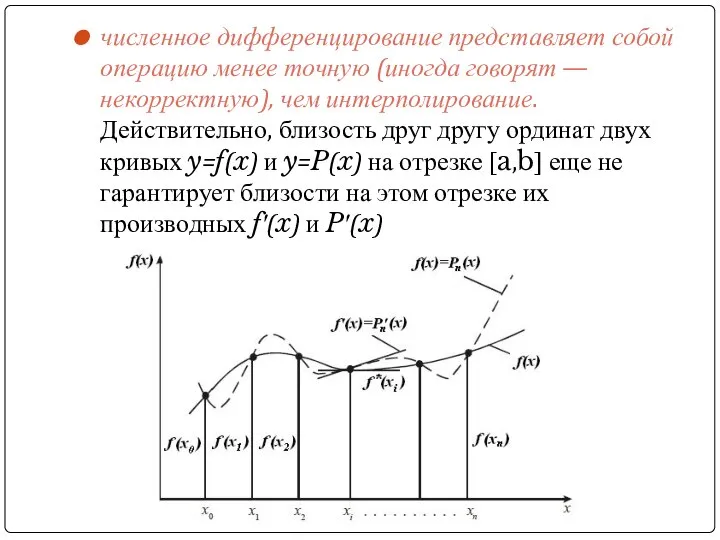
- 14. численное дифференцирование представляет собой операцию менее точную (иногда говорят — некорректную), чем интерполирование. Действительно, близость друг
- 15. Интерполяция конечными разностями В этом случае (x*= xi , i = 0,…, n) используется аппарат разложения
- 16. Выразим yi’, разделив предварительно на h и оставляя слагаемые с первой степенью шага h, получим
- 17. где — центральная разность первого порядка
- 18. Метод Рунге С целью оценки погрешности продифференцируем численно методом p-го порядка функцию f(xi) = yi ,
- 20. Скачать презентацию














 Сумма углов треугольника. 7 класс
Сумма углов треугольника. 7 класс Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса
Нестандартные задачи как средство формирования исследовательских умений обучающихся в курсе алгебры 8 класса Таблица умножения на шесть. (3 класс)
Таблица умножения на шесть. (3 класс) Решение квадратных неравенств
Решение квадратных неравенств Устойчивость узла нагрузки
Устойчивость узла нагрузки Приведение дробей к новому знаменателю
Приведение дробей к новому знаменателю Исследование функции. Геометрический смысл производной
Исследование функции. Геометрический смысл производной Итоговое повторение курса алгебры за 8 класс
Итоговое повторение курса алгебры за 8 класс Основы высшей математики и математической статистики
Основы высшей математики и математической статистики Примеры решения тригонометрических уравнений
Примеры решения тригонометрических уравнений Условная вероятность
Условная вероятность Дифференциальным уравнением
Дифференциальным уравнением Математические задачи в стихах
Математические задачи в стихах Аттестационная работа. Программа элективного курса по математике Наглядная геометрия. (5-6 класс)
Аттестационная работа. Программа элективного курса по математике Наглядная геометрия. (5-6 класс) Симметрия вокруг нас
Симметрия вокруг нас Уравнения. 6 класс
Уравнения. 6 класс Базовые компоненты эконометрики
Базовые компоненты эконометрики Сложение и вычитание чисел в пределах 10
Сложение и вычитание чисел в пределах 10 Теорема Фалеса
Теорема Фалеса Математическое путешествие
Математическое путешествие Математические фокусы
Математические фокусы Параллельные прямые
Параллельные прямые Тест по теме: "Цилиндр"
Тест по теме: "Цилиндр" Деление и умножение положительных и отрицательных чисел. 6 класс
Деление и умножение положительных и отрицательных чисел. 6 класс Законы распределения случайных величин
Законы распределения случайных величин Первый признак равенства треугольников. Математический диктант
Первый признак равенства треугольников. Математический диктант Решение линейных уравнений с параметром и модулем
Решение линейных уравнений с параметром и модулем Таблица умножения на 9
Таблица умножения на 9