Содержание
- 2. Дифференциальным уравнением (ДУ) называется уравнение, содержащее производные от искомой функции или её дифференциалы. или
- 3. Примеры ДУ:
- 4. Наивысший порядок производной, входящей в уравнение, называется порядком ДУ. Решением ДУ называется такая функция, подстановка которой
- 5. Пример 1. Показать, что данная функция является решением ДУ
- 6. Решение: Т.о. функции вида являются решениями данного ДУ при любом выборе постоянных С1 и С2: Подставим:
- 7. Дифференциальные уравнения I порядка
- 8. Общим решением ДУ I порядка называется функция , которая зависит от одного произвольного постоянного С. или
- 9. Частным решением ДУ I порядка называется любая функция полученная из общего решения при конкретном значении постоянной
- 10. Пример 2. ДУ: -общее решение частные решения
- 11. Геометрически: Общее решение ДУ есть семейство интегральных кривых на плоскости Оху; Частное решение ДУ -одна кривая
- 12. Задача отыскания конкретного частного решения данного ДУ по начальным данным называется задачей Коши (Cauchy). или Условие,
- 13. Пример 3. Решить задачу Коши: -общее решение Решение: Подставим в общее решение начальные условия: -частное решение
- 14. Теорема существования и единственности решения задачи Коши. Если в уравнении функция f(x,y) и её частная производная
- 15. 1. ДУ I порядка с разделёнными переменными. Если каждая часть ДУ представляет собой произведение некоторого выражения,
- 16. Пример 4. Решить ДУ: Решение: С общее решение: или Геометрически: получили семейство концентрических окружностей с центром
- 17. Пример 5. Решить ДУ: Решение: С общее решение: или х у 0 С=1 С=1 С=3 С=3
- 18. 2. ДУ I порядка с разделяющимися переменными. Уравнения, в которых переменные разделяются, называются ДУ с разделяющимися
- 19. интегрируем:
- 20. Замечание: При проведении почленного деления ДУ на могут быть потеряны некоторые решения. Поэтому следует отдельно решить
- 21. Пример 6. Найти общее и частное решение ДУ: Решение: ⇒ 1) Найдём общее решение ДУ:
- 22. Итак, общее решение ДУ: 2) Найдём частное решение ДУ, если Подставим эти начальные условия в общее
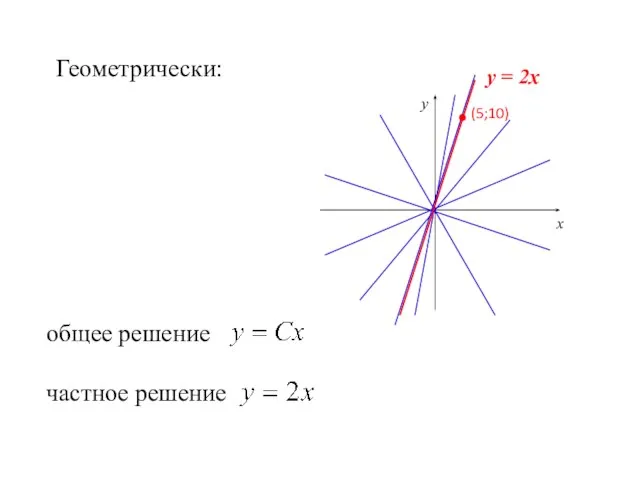
- 23. Геометрически: х у общее решение частное решение у = 2х (5;10)
- 24. Пример 7. Найти общее решение ДУ: Решение:
- 25. или ⇒ Ответ. Общее решение:
- 26. Нахождение особого решения: Здесь уравнение имеет вид ху=0 Его решения х=0, у=0 являются решениями данного ДУ,
- 27. Пример 8. Найти общее решение ДУ: Решение:
- 28. или ⇒
- 29. Геометрически: общее решение С=5 С=3 С=1 С=-2 С=-5 х у
- 30. Пример 9. Решить задачу Коши: Решение: 1) Найдём общее решение ДУ:
- 31. или Итак, общее решение ДУ: С
- 32. 2) Найдём частное решение ДУ, если Подставим эти начальные условия в общее решение и найдем С:
- 33. Геометрически: общее решение частное решение (0;1) С=5 С=-3 С=-6 С=0 х у
- 34. Пример 10. Решить задачу Коши: Решение: 1) Найдём общее решение ДУ:
- 35. Итак, общее решение ДУ: ⇒
- 36. 2) Найдём частное решение ДУ, если Подставим эти начальные условия в общее решение и найдем С:
- 38. Скачать презентацию

















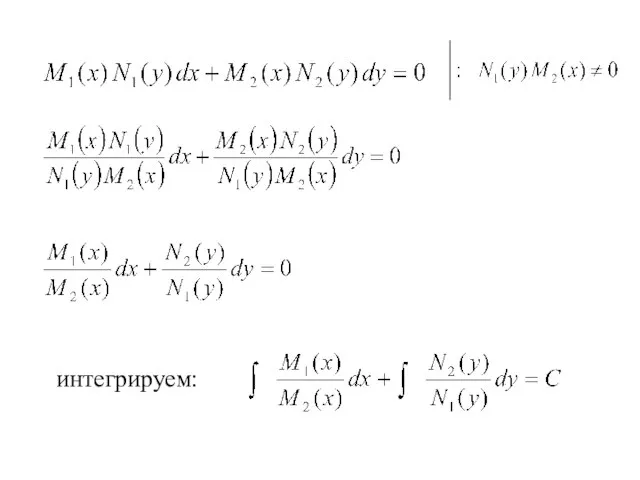
















 Оптимальные назначения, использующие вектор неоднородных критериев
Оптимальные назначения, использующие вектор неоднородных критериев Дрейфовое приближение. Виды дрейфового движения. Общие свойства
Дрейфовое приближение. Виды дрейфового движения. Общие свойства Задачи на увеличение числа на несколько единиц (с двумя множествами предметов). Автор: учитель начальных классов МОУ СОШ №24 Столбо
Задачи на увеличение числа на несколько единиц (с двумя множествами предметов). Автор: учитель начальных классов МОУ СОШ №24 Столбо Формулы сокращенного умножения
Формулы сокращенного умножения Презентация по математике "Многогранники в архитектуре" - скачать
Презентация по математике "Многогранники в архитектуре" - скачать  Площадь многоугольников. Теорема Пифагора. Решение задач
Площадь многоугольников. Теорема Пифагора. Решение задач Фракталы в аэрографии
Фракталы в аэрографии Теория преобразования графиков функций
Теория преобразования графиков функций Решение систем неравенств с одной переменной
Решение систем неравенств с одной переменной Открытый урок по алгебре в 11 классе по теме Показательные уравнения
Открытый урок по алгебре в 11 классе по теме Показательные уравнения Конкретизация вида коэффициента эффективной квадратичной нелинейной восприимчивости
Конкретизация вида коэффициента эффективной квадратичной нелинейной восприимчивости Графическое решение задач на равномерное движение
Графическое решение задач на равномерное движение Дробные рациональные уравнения
Дробные рациональные уравнения Окружность (геометрия 7 класс)
Окружность (геометрия 7 класс) Вектори на площині
Вектори на площині Неевклидова геометрия
Неевклидова геометрия Делимость произведения. Урок 99
Делимость произведения. Урок 99 РЕШЕНИЕ ЗАДАЧ Прямая и обратная пропорциональность
РЕШЕНИЕ ЗАДАЧ Прямая и обратная пропорциональность Устная разминка на уроке математики
Устная разминка на уроке математики Все действия с десятичными дробями
Все действия с десятичными дробями Рациональные уравнения. Подготовка к ОГЭ
Рациональные уравнения. Подготовка к ОГЭ Аттестационная работа. Задачи на смеси и сплавы. Метод Пирсона
Аттестационная работа. Задачи на смеси и сплавы. Метод Пирсона Общая начальная математическая подготовка в 1 – 5 классах ТМОМ Общепедагогические основы обучения математике
Общая начальная математическая подготовка в 1 – 5 классах ТМОМ Общепедагогические основы обучения математике Полезные факты и теоремы
Полезные факты и теоремы Фракталы
Фракталы Периметр треугольника
Периметр треугольника Объемы и поверхности многогранников
Объемы и поверхности многогранников Three-point difference derivative
Three-point difference derivative