Содержание
- 2. Если функция f(x) непрерывна на отрезке то определенный интеграл от этой функции в пределах от a
- 3. Найти определенный интеграл на отрезке если подынтегральная функция на отрезке задана таблично. Формулы приближенного интегрирования называются
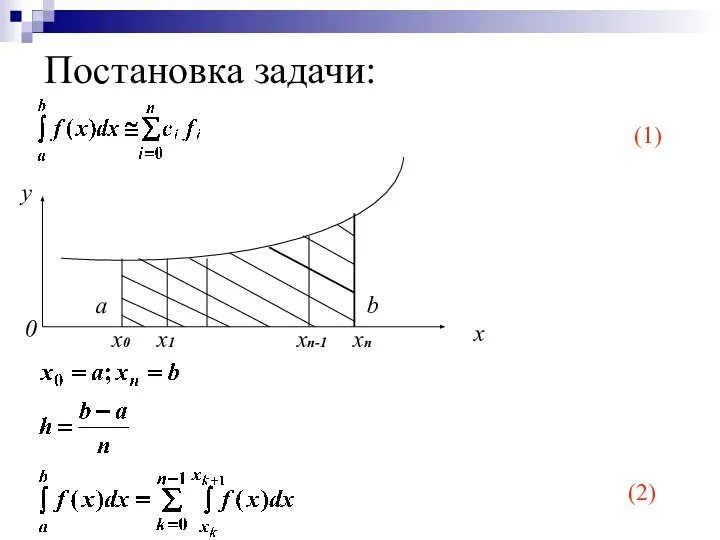
- 4. Постановка задачи: (1) (2) 0 x y a b x0 x1 xn-1 xn
- 5. Погрешность численного интегрирования - погрешность вычисления интеграла - погрешность в целом - погрешность в малом -
- 6. Связь Пусть и
- 7. Метод прямоугольников основан на непосредственном определении интеграла: где - интегральная сумма, соответствующая некоторому разбиению отрезка и
- 8. Вычисление определенного интеграла геометрически сводится к вычислению площади криволинейной трапеции, ограниченной функцией f(x), осью абсцисс и
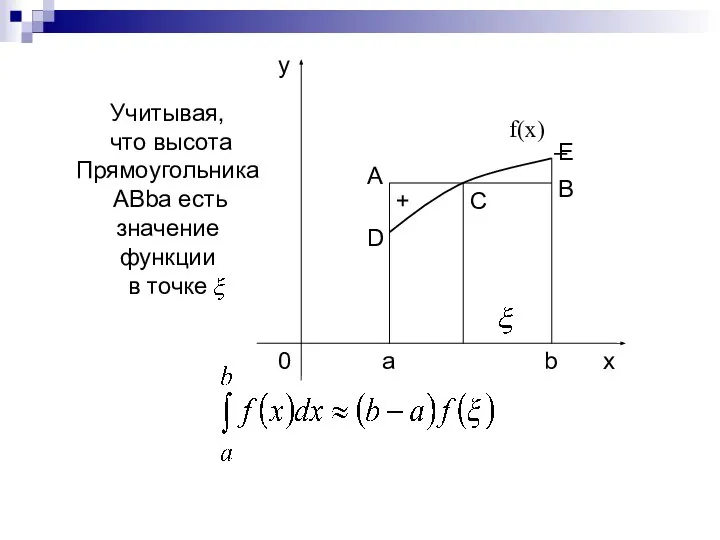
- 9. Учитывая, что высота Прямоугольника ABba есть значение функции в точке f(x) –
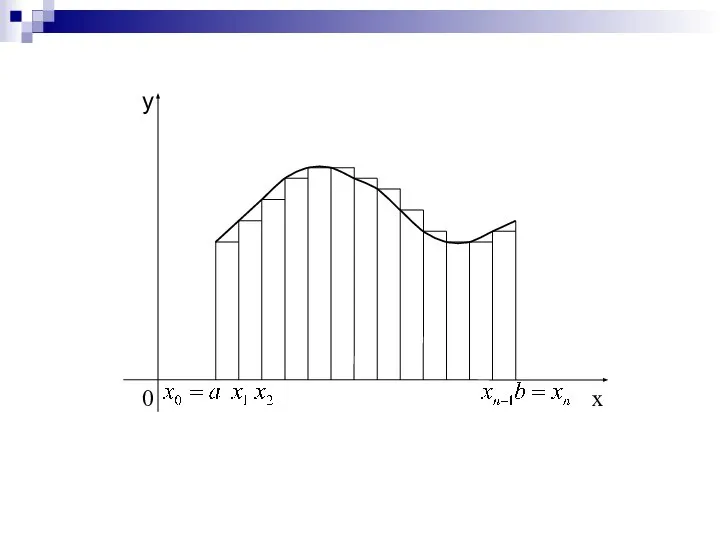
- 10. Для увеличения точности численного интегрирования можно отрезок разбить на несколько частей и для каждой из них
- 11. Практически удобно делить отрезок на равные части, а точки (i = 0, 1, …, n –
- 12. Если точку совместить с левым концом отрезка то приближенное значение интеграла может быть представлено формулой левых
- 14. Если же в качестве точки выбрать правый конец отрезка то приближенное значение интеграла вычисляется по формуле
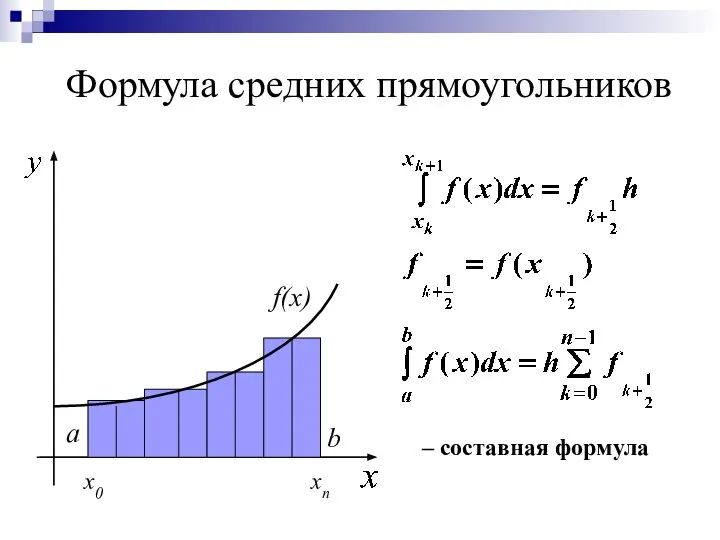
- 16. Формула средних прямоугольников a b f(x) x0 xn – составная формула
- 17. Погрешность формул средних прямоугольников
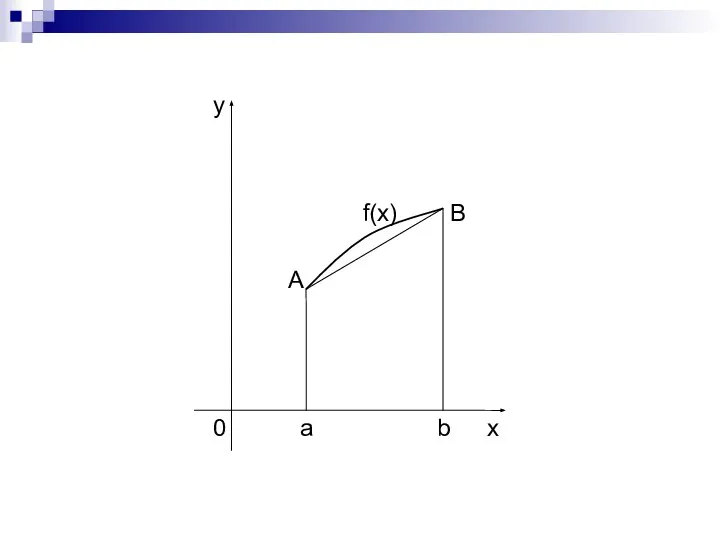
- 18. Метод трапеций Заменим на отрезке дугу AB графика подынтегральной функции y = f(x) стягивающей ее хордой
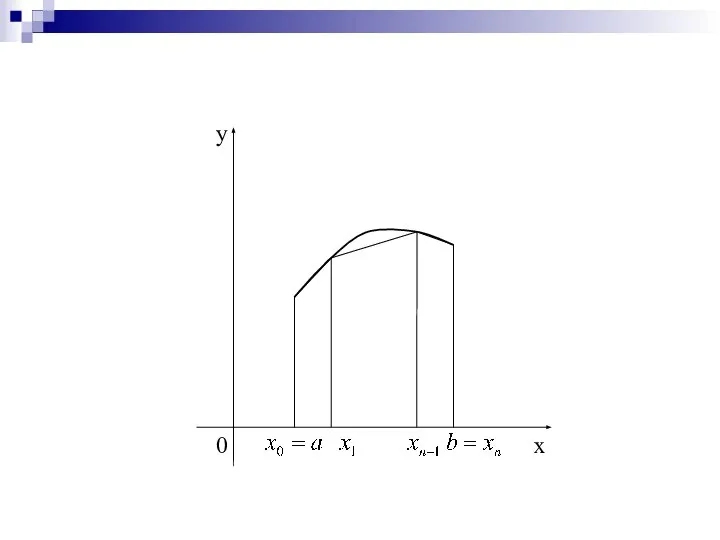
- 20. Если отрезок разделить на несколько частей и применить формулу трапеции к каждому отрезку Тогда
- 22. Для простоты вычислений удобно разделить отрезок на равные части, в этом случае длина каждого из отрезков
- 23. А на всем отрезке соответственно Эта формула называется общей формулой трапеции. Ее можно переписать в виде
- 24. Погрешность формулы трапеций
- 25. Составная формула трапеции
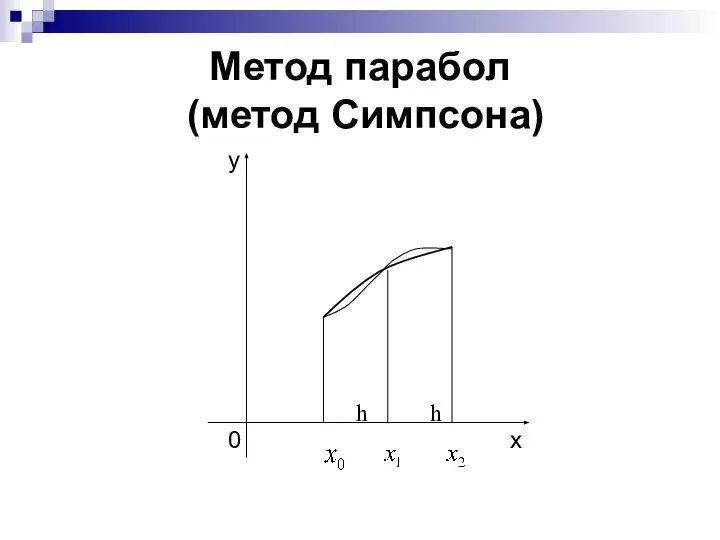
- 26. Метод парабол (метод Симпсона) h h
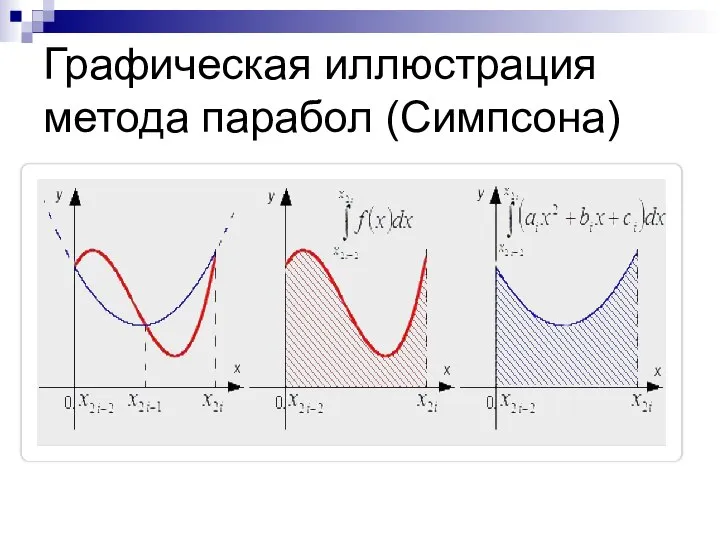
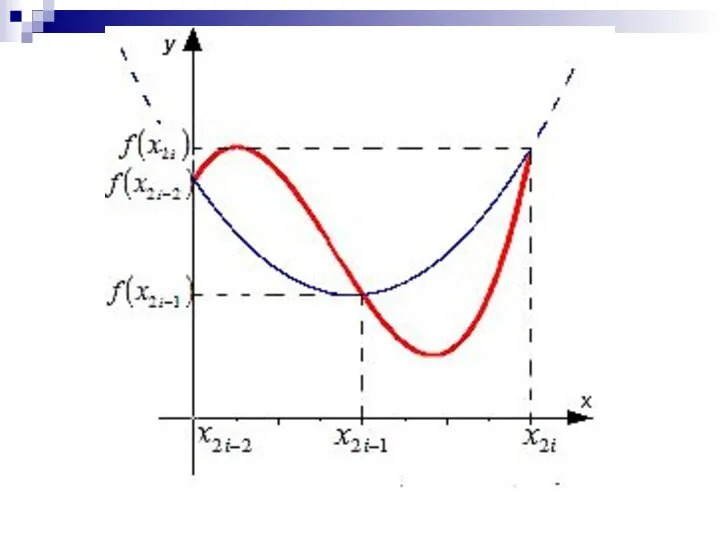
- 27. Графическая иллюстрация метода парабол (Симпсона)
- 28. Формула Симпсона
- 30. Определитель матрицы отличен от 0 => система уравнений имеет единственное решение
- 31. Через данные точки проходит единственная квадратичная парабола
- 32. Вычислим значение функции в точках
- 33. Найдём интеграл
- 34. Для увеличения точности вычислений отрезок разбивают на n пар участков и заменяя подынтегральную функцию интерполяционным многочленом
- 35. ……………………………………
- 36. Тогда численное значение определенного интеграла на отрезке будет равно сумме интегралов Это соотношение называется общей формулой
- 37. Составная формула Симпсона
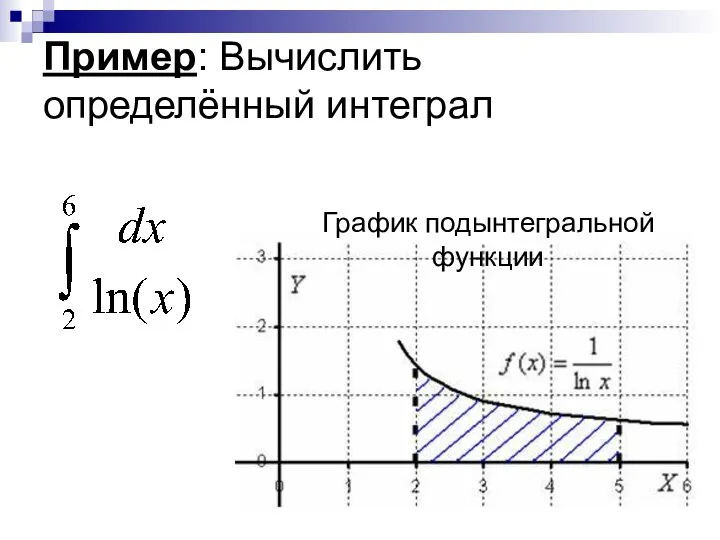
- 38. Пример: Вычислить определённый интеграл График подынтегральной функции
- 39. Ответ:
- 40. Метод Монте-Карло Методы Монте-Карло – это общее название группы методов для решения различных задач с помощью
- 41. Сущность метода Монте-Карло состоит в следующем: Требуется найти значение а некоторой изучаемой величины. Для этого выбирают
- 42. Пример использования метода Монте-Карло Предположим, что нам нужно определить площадь плоской фигуры, расположенной внутри квадрата, сторона
- 44. Скачать презентацию



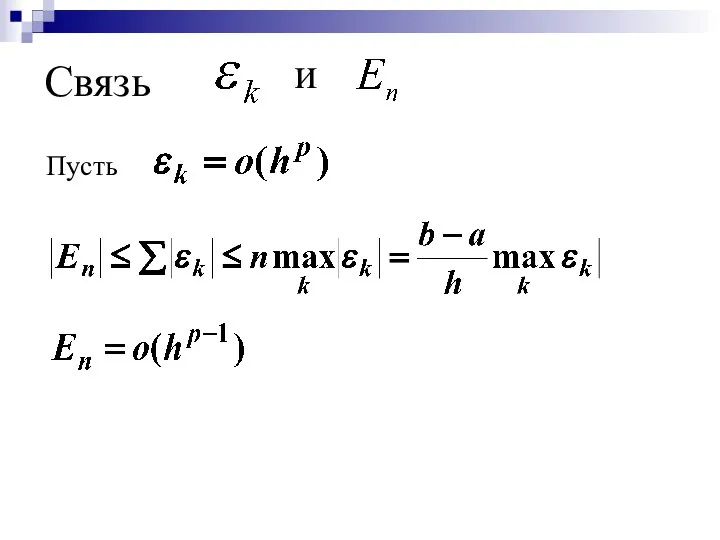



























 Методы и модели корреляционно-регрессионного анализа. Лекция 2
Методы и модели корреляционно-регрессионного анализа. Лекция 2 Умножение натуральных чисел и его свойства
Умножение натуральных чисел и его свойства Временные ряды и их предварительный анализ
Временные ряды и их предварительный анализ Буквенные выражения
Буквенные выражения Геометрия. Треугольники
Геометрия. Треугольники Итерактивная мозаика
Итерактивная мозаика Пирамиды. Решение задач
Пирамиды. Решение задач Линейные дифференциальные уравнения n-го порядка
Линейные дифференциальные уравнения n-го порядка Интеллектуальная игра Математика
Интеллектуальная игра Математика Умножение и деление степеней. Основное свойство степени
Умножение и деление степеней. Основное свойство степени Графы. Эйлеровы графы. Гамильтоновы графы. Изоморфизмы графов
Графы. Эйлеровы графы. Гамильтоновы графы. Изоморфизмы графов Показательные неравенства
Показательные неравенства Модуль числа. Урок математики в 6 классе
Модуль числа. Урок математики в 6 классе Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану
Физикалық дамуды бағалау үшін регрессия және корреляцияны қолдану Площадь многоугольника. Свойства площадей. Готовимся к ОГЭ
Площадь многоугольника. Свойства площадей. Готовимся к ОГЭ Письменные приемы сложения и вычитания. Закрепление
Письменные приемы сложения и вычитания. Закрепление Математикалық патшалығы
Математикалық патшалығы Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений Тригонометрические неравенства
Тригонометрические неравенства Презентация по математике "Угол поворота. Радианная мера угла" - скачать бесплатно
Презентация по математике "Угол поворота. Радианная мера угла" - скачать бесплатно Презентация на тему Сложение и вычитание трехзначных чисел
Презентация на тему Сложение и вычитание трехзначных чисел  Основное тригонометрическое тождество. Формулы приведения
Основное тригонометрическое тождество. Формулы приведения Задачи на переливание жидкости
Задачи на переливание жидкости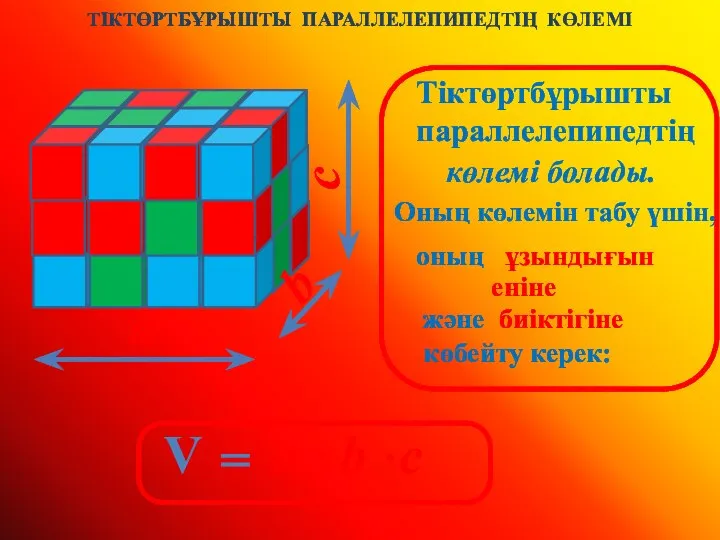 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Учебный элемент Наименование:
Учебный элемент Наименование: Взаимно простые числа. Признак делимости
Взаимно простые числа. Признак делимости Мастер-класс «Использование презентаций PowerPoint на уроках математики при построении графиков функции»
Мастер-класс «Использование презентаций PowerPoint на уроках математики при построении графиков функции» Арифметическая прогрессия
Арифметическая прогрессия