Содержание
- 2. Численное дифференцирование и интегрирование функций 5.1. Постановка вопроса Найти производные указанных порядков от функции f(x), заданной
- 3. 5.2. Приближенное дифференцирование на основе первой интерполяционной формулы Ньютона Пусть функция y(x) задана в равноотстоящих точках
- 4. Перемножая биномы получим Учтем Далее, поскольку В результате: получим Аналогично можно получить формулы и для производных
- 5. 5.3. Приближенное дифференцирование для равноотстоящих точек (узлов), выраженных через значения функций в этих точках на основе
- 6. Полагая получим Тогда, для полинома Лагранжа имеем Учитывая то, что Получаем
- 7. Погрешность вычисления первой производной: Для Rn получим Тогда, Если число узлов нечетно и производная берется в
- 8. 5.4. Приближенное интегрирование функций. Общие замечания Если функция f(x) непрерывна на отрезке [a,b] и известна ее
- 9. Пусть функция y = f(x) задана на отрезке [a,b]. С помощью точек x0, x1…, xn разобьем
- 10. 5.7. Метод трапеций В этом методе используется линейная интерполяция функции y=f(x) в промежутках между узлами. (i=1,
- 11. 5.8. Уточненные значения интегралов Погрешность численного метода в общем случае равна Главный член погрешности интеграла (I1),
- 12. 5.9. Метод парабол (метод Симпсона) Разобьем отрезок интегрирования [a,b] на четное число n равных частей с
- 13. Просуммировав все отрезки, получим: Значение S принимается в качестве определенного интеграла. Окончательное выражение для формулы Симпсона
- 14. 5.10. Формула Ньютона-Кортеса Пусть для данной функции y=f(x) необходимо вычислить определенный интеграл. где Ai – некоторые
- 15. где постоянные коэффициента Hi называются коэффициентами Кортеса : Окончательный вид квадратурной формулы Ньютона-Кортеса: где Коэффициенты Кортеса
- 16. Остаточный член формулы Ньютона-Котеса: где E(n/2) – целая часть дроби n/2. Таким образом, нечетное число ординат
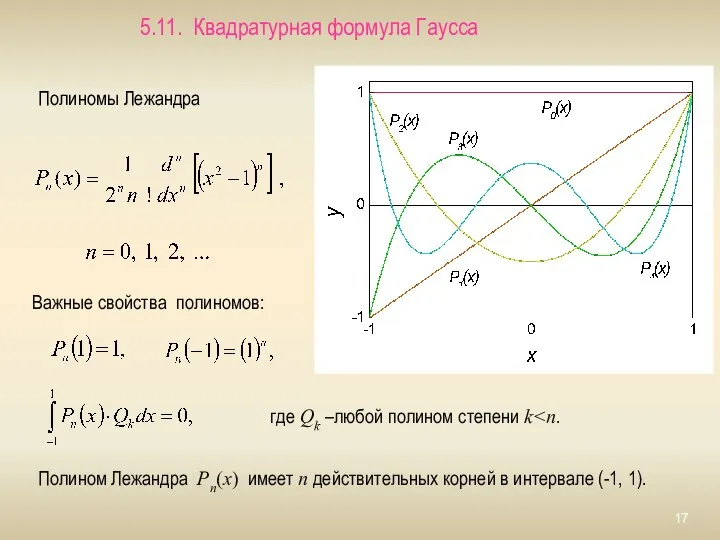
- 17. 5.11. Квадратурная формула Гаусса Полиномы Лежандра Важные свойства полиномов: где Qk –любой полином степени k Полином
- 18. Рассмотрим функцию f(t), заданную на отрезке [-1, 1]. при k четном, Учитывая соотношение при k нечетном
- 19. Так как степени этих полиномов не превышают 2n-1, то на основании системы (2) для них должна
- 20. Подстановка в эту формулу f(t) дает : В силу ортогональности полиномов Лежандра или Это равенство будет
- 21. 5.12. Дифференцирование и интегрирование в пакете MathCad
- 22. 6. Численное решение дифференциальных уравнений 6.1. Основные понятия Дифференциальные уравнения делятся на: обыкновенные (содержащие одну переменную),
- 23. Линейными дифференциальными уравнениями называются уравнения, линейные относительно искомой функции и её производных. Решением дифференциального уравнения всякая
- 24. Для выделения некоторого частного решения линейного дифференциального уравнения первого порядка достаточно задать координаты некоторой точки (x0,y0)
- 25. 6.2.1. Метод Эйлера Решить дифференциальное уравнение dy/dx=f(x,y) численным методом , значит для заданной последовательности аргументов x0,
- 26. 6.2.1. Метод Рунге-Кутта Этот метод является методом повышенной точности. Как и в методе Эйлера yi= yi-1+Δyi-1,
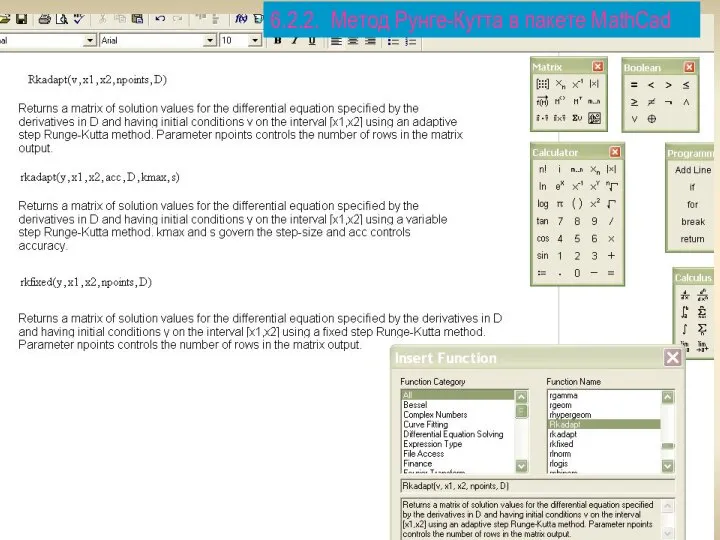
- 27. 6.2.2. Метод Рунге-Кутта в пакете MathCad
- 28. 6.3. Приближенные методы решения краевой задачи для линейного обыкновенного дифференциального уравнения Рассмотрим уравнение вида Краевая задача
- 29. 6.4.1. Метод коллокаций В этом методе выбираются n точек xi, принадлежащих отрезку [a,b], называемых точками коллокации
- 30. 6.4.4. Метод стрельбы Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной. Сущность метода
- 32. Скачать презентацию







![Пусть функция y = f(x) задана на отрезке [a,b]. С помощью](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457031/slide-8.jpg)


![5.9. Метод парабол (метод Симпсона) Разобьем отрезок интегрирования [a,b] на четное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457031/slide-11.jpg)




![Рассмотрим функцию f(t), заданную на отрезке [-1, 1]. при k четном,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1457031/slide-17.jpg)










 Сложение 20. Пчелки
Сложение 20. Пчелки Средства измерений
Средства измерений Лесная школа. Табличное умножение
Лесная школа. Табличное умножение Решение задач
Решение задач Переміщення та його властивості
Переміщення та його властивості Тест по теме: Тригонометрия (теория)
Тест по теме: Тригонометрия (теория) Уравнения - следствия
Уравнения - следствия Квадратный трехчлен и его корни
Квадратный трехчлен и его корни Объемы фигур. Подготовка к ЕГЭ
Объемы фигур. Подготовка к ЕГЭ Четырёхугольники. Сказка - вопрос
Четырёхугольники. Сказка - вопрос Описанная окружность
Описанная окружность Презентация по математике "УРАВНЕНИЯ В ЕГЭ ПО МАТЕМАТИКЕ ПРИМЕРЫ И РЕШЕНИЯ" - скачать
Презентация по математике "УРАВНЕНИЯ В ЕГЭ ПО МАТЕМАТИКЕ ПРИМЕРЫ И РЕШЕНИЯ" - скачать  Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Формулы суммы и разности синуса и косинуса
Формулы суммы и разности синуса и косинуса Складне висловлювання
Складне висловлювання Умножение однозначных чисел на многозначные
Умножение однозначных чисел на многозначные Таблица сложения и вычитания с числом 2
Таблица сложения и вычитания с числом 2 Вычисление площадей плоских фигур
Вычисление площадей плоских фигур Пирамида
Пирамида Свойство биссектрисы угла
Свойство биссектрисы угла Перетворення та переміщення подібності. (9 клас)
Перетворення та переміщення подібності. (9 клас) Сложение и вычитание смешанных дробей
Сложение и вычитание смешанных дробей Умножение десятичных дробей на натуральное число
Умножение десятичных дробей на натуральное число Урок- практикум «Исследование функции с помощью производной» 10 класс
Урок- практикум «Исследование функции с помощью производной» 10 класс Линейное уравнение с двумя неизвестными. 7 класс
Линейное уравнение с двумя неизвестными. 7 класс Урок математики 2 класс
Урок математики 2 класс  Сравнение дробей. 5 класс
Сравнение дробей. 5 класс Статистический анализ результатов моделирования
Статистический анализ результатов моделирования