Содержание
- 2. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
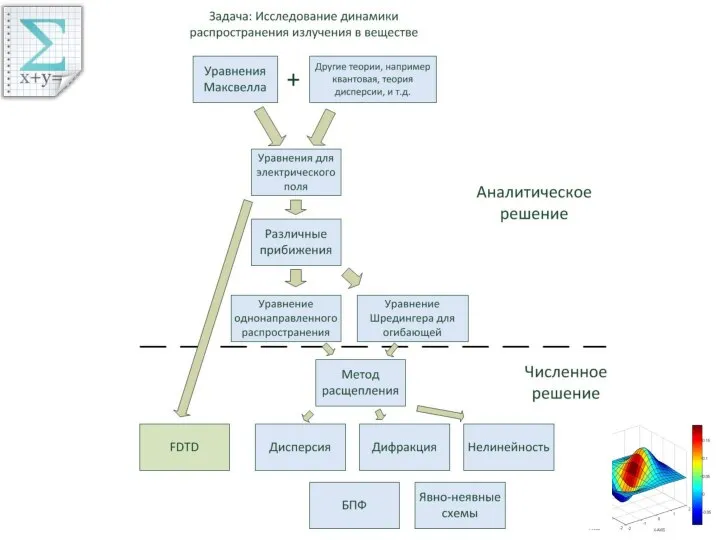
- 3. Цель решения уравнений Современные оптические системы представляют собой сложные комплексы из различных оптических элементов, в каждом
- 4. Электромагнитная природа света В рамках электромагнитной теории все излучение подчиняется законам Максвелла D - электрическая индукция,
- 5. Уравнения Максвелла При решении оптических задач очень часто отсутствуют свободные заряды и токи: А также вместо
- 6. Уравнения Максвелла Получается система Применяя оператор ротора к третьему уравнению системы и подставляя четвертое, получаем волновое
- 7. Волновое уравнение Максвелла Для решения необходимо знать связь между P и E – материальные уравнения, они
- 8. Материальные уравнения В самом общем виде линейная поляризация зависит от прошлых значений поля в данной точке
- 9. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
- 10. Линейный режим Так как зависимость между PL и E представляет собой свертку ее удобно записывать в
- 11. Линейный режим ε(ω) − Зависимость в общем случае комплексная, она описывает как дисперсию, так и поглощение,
- 12. Вид скалярных уравнений Уравнение Шредингера для огибающей Очень часто α считают равным 0, а также пренебрегают
- 13. Вид скалярных уравнений Уравнение для поля импульса с использованием приближения однонаправленного распространения (без учета дифракции, т.е.
- 14. Вид скалярных уравнений Уравнение для поля импульса с использованием приближения однонаправленного распространения (с учетом дифракции) Здесь
- 15. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
- 16. Нормировка уравнения или
- 17. Отступление про вычислительную точность Дробные числа в памяти компьютера могут иметь одинарную, либо двойную точность Одинарная
- 18. Отступление про вычислительную точность При этом надо помнить, что для компьютера после вычисления a = 1
- 20. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
- 21. Решение методом расщепления по физическим факторам Метод расщепления состоит в последовательном решении
- 22. В случае уравнения с дифракцией для поля
- 23. Дисперсионное уравнение Данное уравнение может быть переписано в спектральной области (применяя преобразование Фурье к каждой из
- 24. Дисперсионное уравнение Либо в более общем виде Можно заменить производную по z конечной разностью (апроксимация первого
- 25. Решение дисперсионного уравнения Однако такое уравнение имеет точное решение
- 26. Решение дисперсионного уравнения Таким образом для решения дисперсионного уравнения необходимо посчитать спектр поля умножить спектр на
- 27. Про преобразование Фурье В случае когда сигнал у нас задан на сетке в виде отсчетов sk
- 28. Отступление про сложность алгоритмов Определение f(n)=O(g(n)) В нашем случае f(n) – количество операций необходимых для расчета
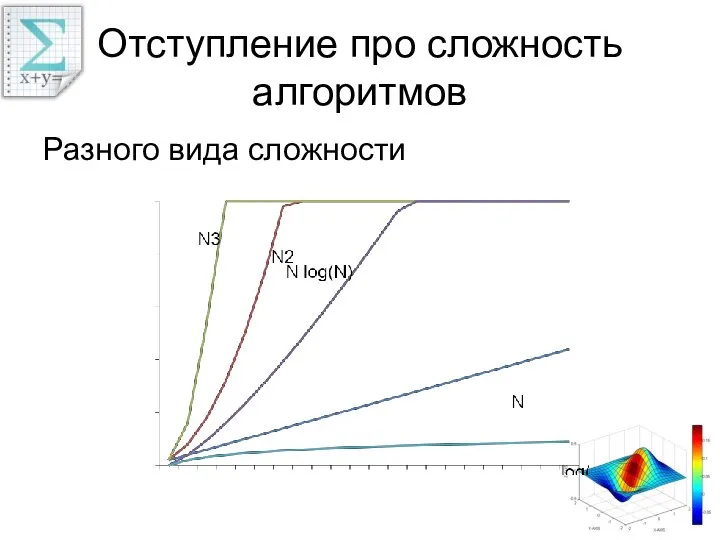
- 29. Сложность алгоритмов вычисления преобразования Фурье Для ДПФ необходимо O(n2) операций, где n – размер массива входных
- 30. Отступление про сложность алгоритмов Разного вида сложности
- 31. БПФ Ограничения накладываемые на данные из-за использования БПФ 1) Равномерная сетка, т.е. ti+1-ti = Δt 2)
- 32. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
- 33. Решение дифракционного уравнения Переходим в спектральную область
- 34. Память и время работы Предположим G у нас зависит от 3 координат и времени, тогда если
- 35. Скорость работы компьютера Одна из характеристик процессоров – тактовая частота, например 3 ГГц, т.е. 3 000
- 36. Скорость работы компьютера Факты влияющие на скорость Тактовая частота Реализация алгоритма Количество тактов на операцию Наличие
- 37. Время работы Таким образом получается значение в районе 300 секунд на шаг алгоритма
- 38. Решение дифракционного уравнения Предположим, что импульс имеет осевую симметрию, т.е. E(t, r, z), G(ω, r, z),
- 39. Решение дифракционного уравнения Сетка по r не обязана быть равномерной!
- 40. Решение дифракционного уравнения схема Кранка-Николсона .
- 41. Схема Кранка-Николсона
- 42. Содержание Описание световых волн. Уравнения для электромагнитных волн. Линейный режим взаимодействия света с веществом. Нормировка динамических
- 43. Материальные уравнения В самом общем виде линейная поляризация зависит от прошлых значений поля в данной точке
- 44. Решение нелинейного уравнения Для вычисления производной можно использовать БПФ, а можно центральную разность Для шага по
- 46. Скачать презентацию









































 Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс По Щучьему велению на новый лад
По Щучьему велению на новый лад Сумма
Сумма Презентация на тему Логарифмы и их свойства
Презентация на тему Логарифмы и их свойства  Сфера и шар
Сфера и шар Подготовка к ОГЭ. Задания по геометрии. Занятие 7
Подготовка к ОГЭ. Задания по геометрии. Занятие 7 Особливості роботи з типами
Особливості роботи з типами Парадоксы теории множеств. (Лекция 9)
Парадоксы теории множеств. (Лекция 9) Формирование навыков письменного сложения и вычитания
Формирование навыков письменного сложения и вычитания Равенство треугольников. Второй признак равенства треугольников
Равенство треугольников. Второй признак равенства треугольников Признаки подобия треугольников
Признаки подобия треугольников Таблица умножения и деления на 6
Таблица умножения и деления на 6 Построение сечений тетраэдра и параллелепипеда
Построение сечений тетраэдра и параллелепипеда Введення поняття кілограм
Введення поняття кілограм Экспериментальные данные. Характеристики выборки и генеральной совокупности. (Лекция 1)
Экспериментальные данные. Характеристики выборки и генеральной совокупности. (Лекция 1) Презентация по математике "Состав чисел от 1 до 10" - скачать бесплатно
Презентация по математике "Состав чисел от 1 до 10" - скачать бесплатно Угол между прямыми в пространстве
Угол между прямыми в пространстве Задачи. (2 класс)
Задачи. (2 класс) Обобщающий урок по теме «Уравнения»
Обобщающий урок по теме «Уравнения» Треугольник. 8 классе
Треугольник. 8 классе Применение нескольких способов разложения многочленов на множители
Применение нескольких способов разложения многочленов на множители Производные и интегралы функций общего вида
Производные и интегралы функций общего вида Метод поиска в глубину. (Лекция 5)
Метод поиска в глубину. (Лекция 5) Обратная пропорциональность
Обратная пропорциональность Конструирование системы заданий для организации продуктивной деятельности учащихся на уроке математики
Конструирование системы заданий для организации продуктивной деятельности учащихся на уроке математики Задачи на доказательство № 25 из ОГЭ (геометрия)
Задачи на доказательство № 25 из ОГЭ (геометрия) Introduction to Statistics
Introduction to Statistics Решение уравнений tgx=a. Понятие арктангенса числа
Решение уравнений tgx=a. Понятие арктангенса числа