Содержание
- 2. СОДЕРЖАНИЕ Текущий контроль Методы наискорейшего спуска (спуск по градиенту) Элементы теории Куна-Таккера
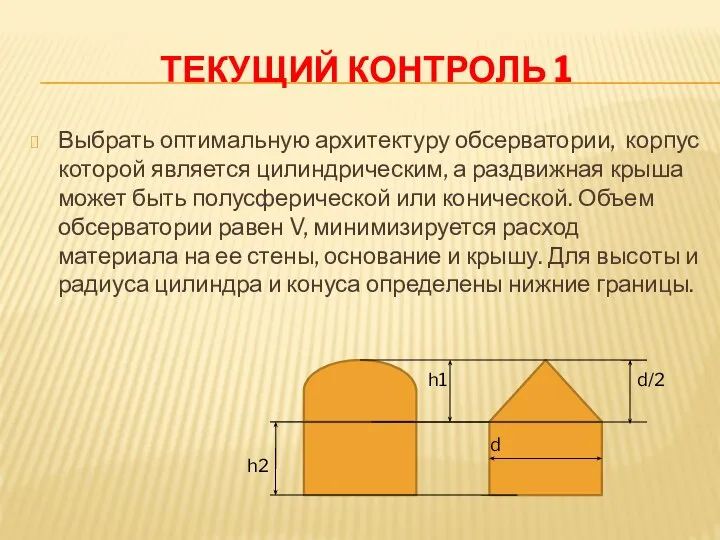
- 3. ТЕКУЩИЙ КОНТРОЛЬ 1 Выбрать оптимальную архитектуру обсерватории, корпус которой является цилиндрическим, а раздвижная крыша может быть
- 4. ТЕКУЩИЙ КОНТРОЛЬ 2 РЕШИТЬ МЕТОДОМ МНОЖИТЕЛЕЙ ЛАГРАНЖА i-порядковый номер студента.
- 5. ПОСТАНОВКА ЗАДАЧИ Задана нелинейная однокритериальная оптимизационная модель вида: Все функции системы (1) являются гладкими и дифференцируемыми,
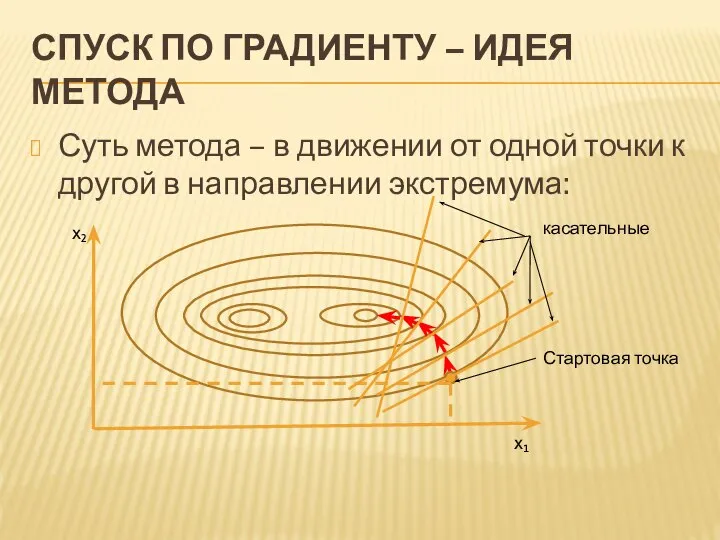
- 6. СПУСК ПО ГРАДИЕНТУ – ИДЕЯ МЕТОДА Суть метода – в движении от одной точки к другой
- 7. АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – ПЕРВЫЕ ДВА ШАГА (ВСЕГО 10 ШАГОВ) Шаг 1. Вычисляется значение функции
- 8. АЛГОРИТМ СПУСКА ПО ГРАДИЕНТУ – СЛЕДУЮЩИЕ ЧЕТЫРЕ ШАГА Шаг 3. Вычисляется новое значение целевой функции f₁.
- 9. ПОСЛЕДНИЕ ЧЕТЫРЕ ШАГА АЛГОРИТМА Шаг 7. Старые значения переменных заменяются на новые, полученные на шаге 2
- 10. ПРИМЕР 1 Пользуясь спуском по градиенту решить задачу: Точка старта: х=у=3; f=0,66, начальная величина шага β=1,
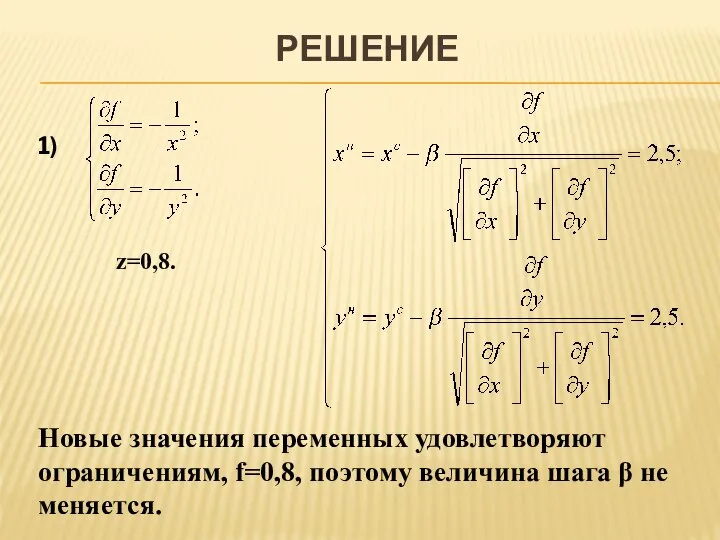
- 11. РЕШЕНИЕ 1) z=0,8. Новые значения переменных удовлетворяют ограничениям, f=0,8, поэтому величина шага β не меняется.
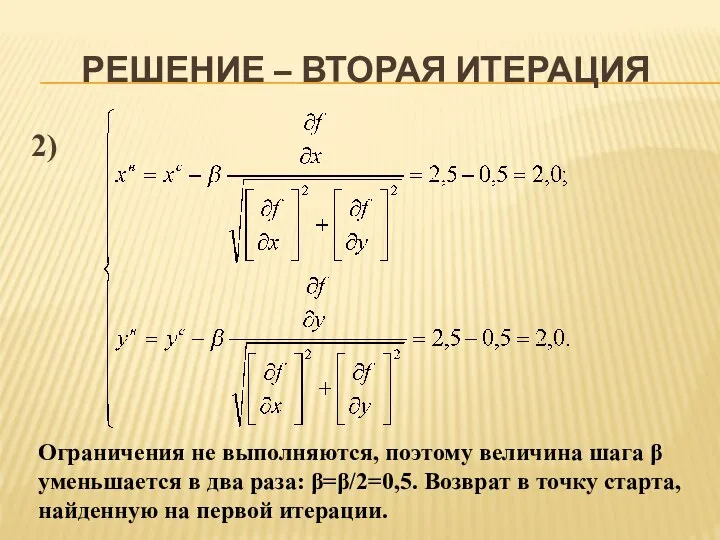
- 12. РЕШЕНИЕ – ВТОРАЯ ИТЕРАЦИЯ 2) Ограничения не выполняются, поэтому величина шага β уменьшается в два раза:
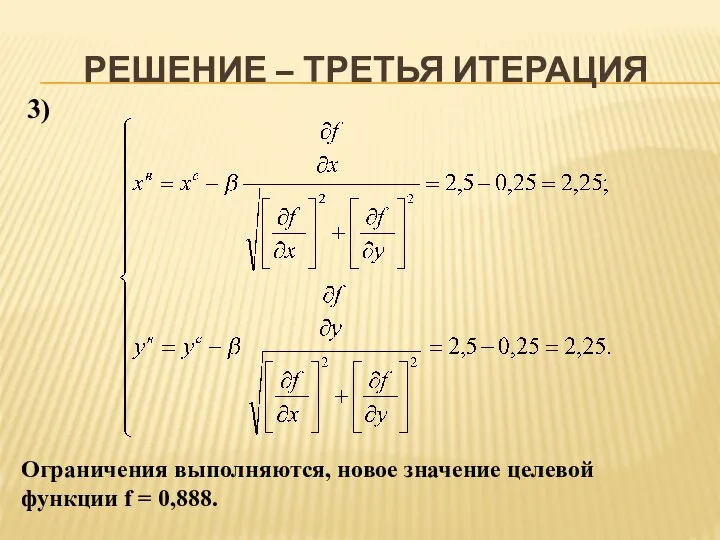
- 13. РЕШЕНИЕ – ТРЕТЬЯ ИТЕРАЦИЯ 3) Ограничения выполняются, новое значение целевой функции f = 0,888.
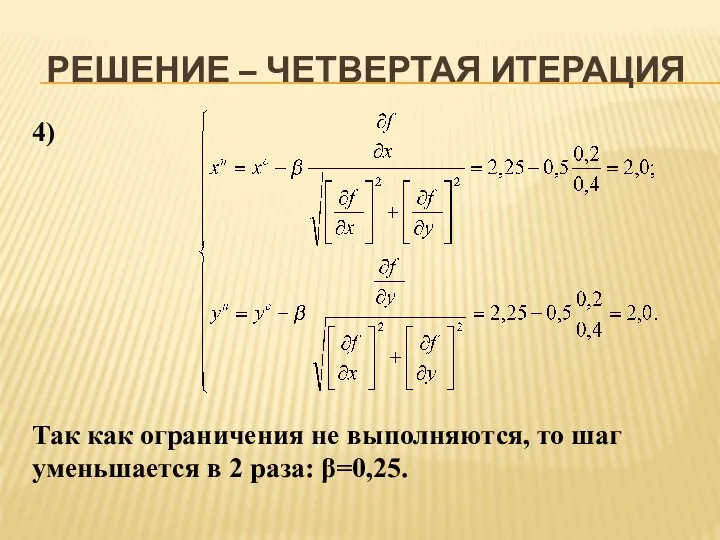
- 14. РЕШЕНИЕ – ЧЕТВЕРТАЯ ИТЕРАЦИЯ 4) Так как ограничения не выполняются, то шаг уменьшается в 2 раза:
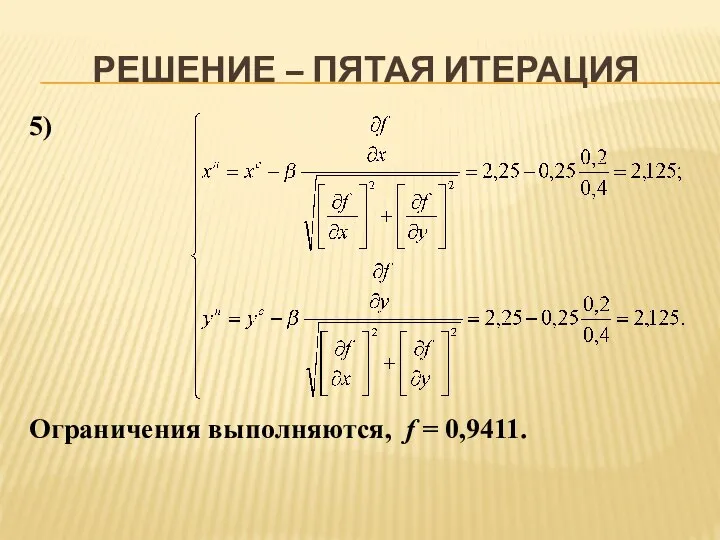
- 15. РЕШЕНИЕ – ПЯТАЯ ИТЕРАЦИЯ 5) Ограничения выполняются, f = 0,9411.
- 16. РЕШЕНИЕ – ШЕСТАЯ ИТЕРАЦИЯ 6) Значения переменных не удовлетворяют ограничению, шаг β уменьшается в два раза,
- 17. САМОСТОЯТЕЛЬНО Пользуясь приведенным выше алгоритмом решить задачу (2): Решить задачи (1) и (2), пользуясь методом множителей
- 18. ОПРЕДЕЛЕНИЕ ВЫПУКЛЫХ ФУНКЦИЙ Функция f называют выпуклой на интервале [a,b] если для любой точки отрезка, соединяющего
- 19. ОПРЕДЕЛЕНИЕ ВОГНУТЫХ ФУНКЦИЙ Функция f называют вогнутой на интервале [a,b] если для любой точки отрезка, соединяющего
- 20. ОПРЕДЕЛЕНИЯ ГЛОБАЛЬНОГО И ЛОКАЛЬНОГО ОПТИМУМА Функция называется локально оптимальной в точке «х» , если все значения
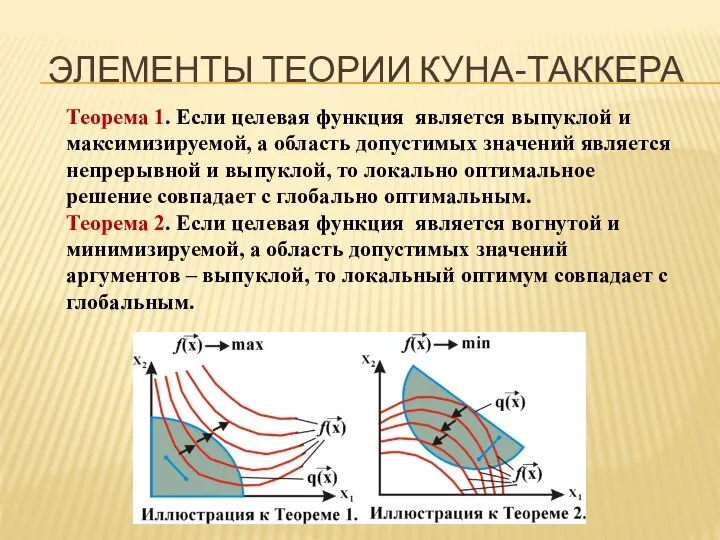
- 21. ЭЛЕМЕНТЫ ТЕОРИИ КУНА-ТАККЕРА Теорема 1. Если целевая функция является выпуклой и максимизируемой, а область допустимых значений
- 22. САМОСТОЯТЕЛЬНО Определить являлись ли решения задач (1) и (2), полученные выше спуском по градиенту, глобально оптимальными.
- 23. ПОИСК ПО ГРАДИЕНТУ С ИЗМЕНЯЕМОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ. 1. Определена задача: 2. Осуществляется спуск в лучшем направлении
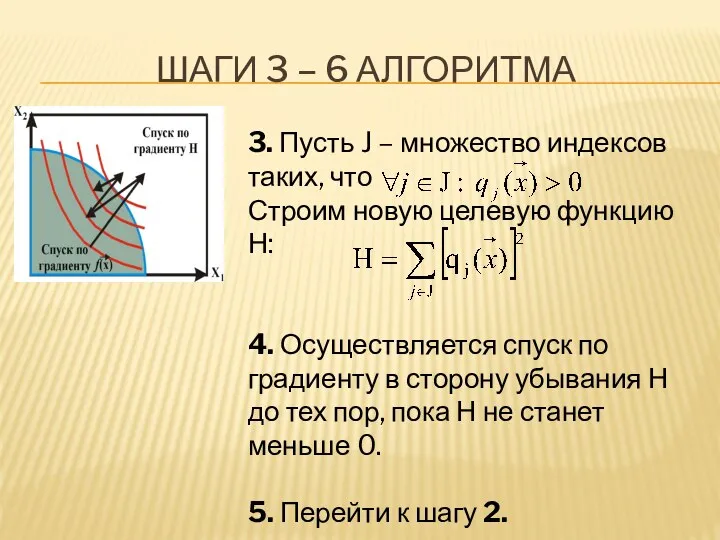
- 24. ШАГИ 3 – 6 АЛГОРИТМА 3. Пусть J – множество индексов таких, что Строим новую целевую
- 26. Скачать презентацию









![ОПРЕДЕЛЕНИЕ ВЫПУКЛЫХ ФУНКЦИЙ Функция f называют выпуклой на интервале [a,b] если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1467084/slide-17.jpg)
![ОПРЕДЕЛЕНИЕ ВОГНУТЫХ ФУНКЦИЙ Функция f называют вогнутой на интервале [a,b] если](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1467084/slide-18.jpg)



 Сложение чисел с помощью координатной прямой
Сложение чисел с помощью координатной прямой Вычисление производных
Вычисление производных Повторение. Алгебра 9 класс (урок 4)
Повторение. Алгебра 9 класс (урок 4) Распределительный закон. История возникновения
Распределительный закон. История возникновения Обратная матрица
Обратная матрица Задачи по математике
Задачи по математике Аттестационная работа. Образовательная программа общеинтеллектуального направления В мире математики
Аттестационная работа. Образовательная программа общеинтеллектуального направления В мире математики Применение математических методов для решения содержательных задач из различных областей науки и практики
Применение математических методов для решения содержательных задач из различных областей науки и практики Поговорим о нуле
Поговорим о нуле Численное моделирование сечений скалярных полей на конечно-элементных сетках
Численное моделирование сечений скалярных полей на конечно-элементных сетках Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов
Понятие алгоритма. Свойства алгоритмов. Формы записей алгоритмов. Общие принципы построения алгоритмов Бесконечно убывающая геометрическая последовательность и ее сумма
Бесконечно убывающая геометрическая последовательность и ее сумма Прямоугольник
Прямоугольник Факторный анализ
Факторный анализ Таблица умножения на пальцах
Таблица умножения на пальцах Проектная деятельность в школе как показатель сформированности познавательных УУД
Проектная деятельность в школе как показатель сформированности познавательных УУД Углы
Углы Формулы производной тангенса и котангенса
Формулы производной тангенса и котангенса Прямоугольник. Ось симметрии фигуры
Прямоугольник. Ось симметрии фигуры Округление дробей
Округление дробей Фигуры: плоские и объёмные
Фигуры: плоские и объёмные Событие, вероятность события. Сложение и умножение вероятностей. Понятие о независимости событий
Событие, вероятность события. Сложение и умножение вероятностей. Понятие о независимости событий Элементы теории ошибок измерений. Лекция №6
Элементы теории ошибок измерений. Лекция №6 Величины и их измерение
Величины и их измерение Использование производной для исследования функций и построения графиков. 11 класс
Использование производной для исследования функций и построения графиков. 11 класс Площадь круга
Площадь круга Из истории геометрии
Из истории геометрии Раскрытие скобок и заключение в скобки
Раскрытие скобок и заключение в скобки