Содержание
- 2. Обратная матрица. Матрица В называется обратной к матрице А если AB =BA = E; при этом
- 3. Алгоритм нахождения обратной матрицы А-1 1. Вычислить определитель . Если , то матрица А имеет обратную.
- 4. Пример. Найти А-1, если Решение. det A = 4 - 6 = -2 Следовательно А-1, существует
- 5. Замечание. Можно показать, что, для невырожденной матрицы второго порядка обратная матрица имеет вид: © материалы подготовлены
- 6. Пример. Дана матрица найти А-1, если Решение. 1. Следовательно А-1, существует 2. Найдем алгебраические дополнения: ©
- 7. 3. Заменим все элементы матрицы А на их алгебраические дополнения и транспонируем полученную матрицу, получим 4.
- 8. Выполним проверку © материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
- 9. Другой подход к нахождению обратной матрицы: Пусть дана невырожденная матрица n порядка: Составим из матрицы А
- 10. Пример. Найти матрицу, обратную матрице Решение Припишем справа к матрице А единичную Далее приведем матрицу к
- 11. © материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко Итак, матрица приведена к ступенчатому виду. Добьемся того, чтобы
- 12. Таким образом, матрица А-1= © материалы подготовлены к.ф.-м.н., доц. Н.А. Фоменко
- 13. Cвойства обратных матриц. 1) (A-1)-1 = A; 2) (AB)-1 = B-1A-1 3) (AT)-1 = (A-1)T. Матричные
- 14. Матричный метод решения систем линейных уравнений. Матричный метод применим к решению систем уравнений, где число уравнений
- 15. Пример . Решить систему матричным способом Решение. Обратная матрица существует, так как © материалы подготовлены к.ф.-м.н.,
- 17. Скачать презентацию














 Сети и потоки
Сети и потоки Математическое моделирование автоматических систем регулирования
Математическое моделирование автоматических систем регулирования Метод координат и метод векторов при решении задач
Метод координат и метод векторов при решении задач Проценты. Обыкновенные и десятичные дроби
Проценты. Обыкновенные и десятичные дроби Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Школа Квентин – подготовка к ЕГЭ
Школа Квентин – подготовка к ЕГЭ Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Треугольник. Геометрия 7 класс. Урок решения задач
Треугольник. Геометрия 7 класс. Урок решения задач Неравенства с одной переменной
Неравенства с одной переменной Ешение систем линейных уравнений методом крамера
Ешение систем линейных уравнений методом крамера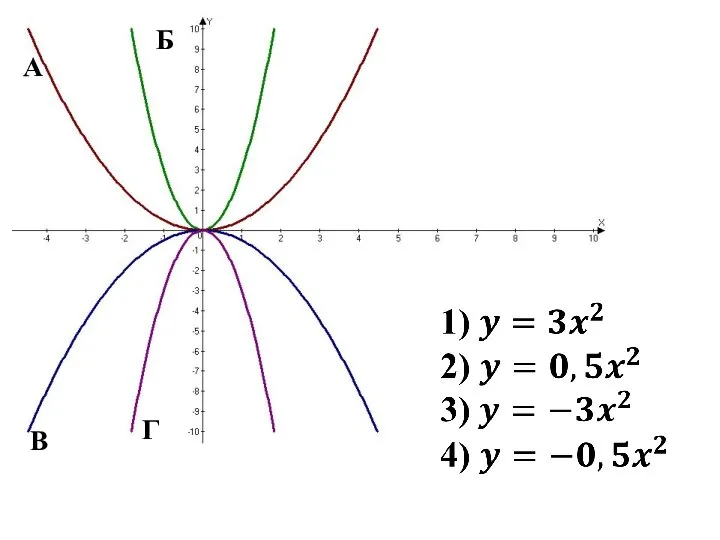 Парабола, гипербола
Парабола, гипербола Великий ученый древнего мира – Архимед и его закон
Великий ученый древнего мира – Архимед и его закон Взаимное расположение Прямых и Плоскостей в пространстве
Взаимное расположение Прямых и Плоскостей в пространстве Математика. Повторение. 1 класс
Математика. Повторение. 1 класс Основы логики. Таблица истинности. Равносильные логические выражения
Основы логики. Таблица истинности. Равносильные логические выражения Понятие, задачи корреляционно-регрессионного анализа и моделирования
Понятие, задачи корреляционно-регрессионного анализа и моделирования Виды треугольников
Виды треугольников Предикати та їх різновиди
Предикати та їх різновиди Из опыта работы учителя математики ГБОУ СОШ с.Курумоч Хохловой Г.В.
Из опыта работы учителя математики ГБОУ СОШ с.Курумоч Хохловой Г.В.  Единицы измерения площадей.
Единицы измерения площадей. МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ
МАТЕМАТИКА, 2 КЛАСС программа «Школа России» УМК «Школа России» «ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО СЛОЖЕНИЯ» Автор: Рябова И.В. МОУСОШ Задачи на построение
Задачи на построение Методы простых средних и скользящих средних
Методы простых средних и скользящих средних Смежные и вертикальные углы
Смежные и вертикальные углы Национальный стандарт по библиотечной статистике: преемственность и новые подходы
Национальный стандарт по библиотечной статистике: преемственность и новые подходы Таблица умножения и деления на 2
Таблица умножения и деления на 2 Статистика. Основные этапы статистического анализа
Статистика. Основные этапы статистического анализа Перпендикулярные прямые
Перпендикулярные прямые