Содержание
- 2. Содержание Конечные случайные величины Совместное распределение Математическое ожидание Дисперсия и среднеквадратичное отклонение Ковариация и коэффициент корреляции
- 3. Конечная случайная величина Ω: A = → X(ω) = ⇒ закон распределения конечной случайной величины
- 4. Примеры* 1. (М) X: {количество «орлов»} = 0 и 1, p = ½ 2. Постоянная случайная
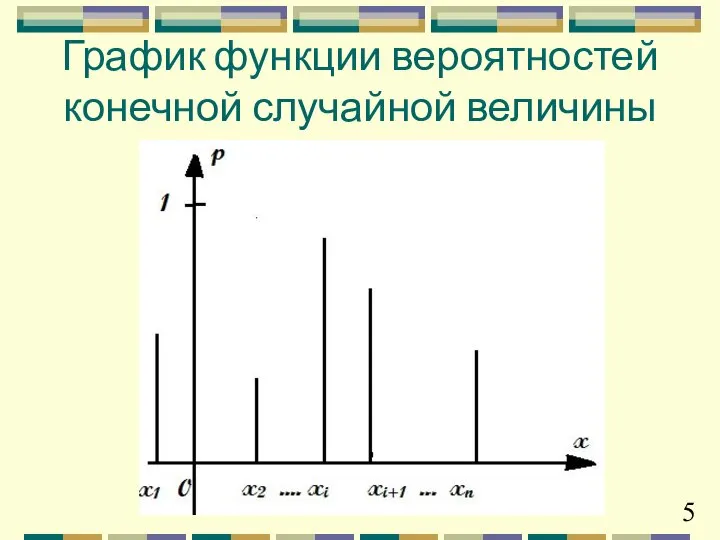
- 5. MIq_307 График функции вероятностей конечной случайной величины
- 6. Совместное распределение X Совместные вероятности Совместное распределение ({хi, уj}; pij)
- 7. Таблица совместного распределения
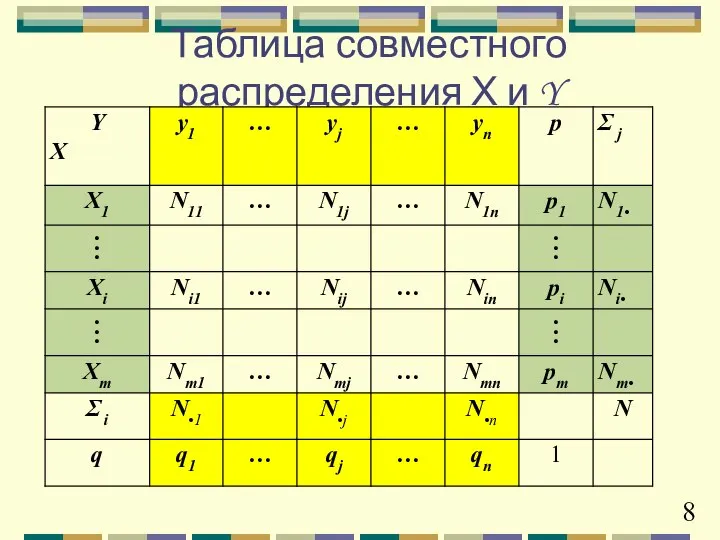
- 8. Таблица совместного распределения Х и Y
- 9. Совместное распределение ∑pij (j = 1…n) = pi , ∑pij (i = 1…n) = qj 3ная
- 10. Независимые X X, Y – независимы ≡{X= хi}, {Y=уj}независимы, i=1,2, ..., т; j=1, 2, ..., п;
- 11. Пусть независимые X1 , X2 , …….., Xn бернуллиевы случайные величины: ⇒ Bn,p = X1 +
- 12. Свойства: 1. Мс = с ⇒ Мс = с • 1 = с 2. X≥ 0
- 13. Bn,p = X1 + X2 + … + Xn Бернуллиевы величины ⇒ MBn,p= MX1 + MX2
- 14. U: {W=4, B=6} наугад вынимают шар и возвращают обратно. Опыт повторяют 10 раз = W шар.
- 15. M(X – MX) = MX – M(MX) = MX - MX = 0 Центрированная Y =
- 16. Дисперсия Случайная величина распределена по закону
- 17. Среднеквадратичное отклонение σ2(x) ∨ σx2 ∨ стандартное отклонение X Свойства: DX ≥ 0 D(cX) = c2DX
- 18. Пример с U… U: B=3, W=2. Из U наугад вынимают 2 шара. X — число W
- 19. Dbn,p = DX1 + DX2 + …+ DXn ∧ X2 = X и MX = MX2
- 20. не меняет дисперсии Случайная величина называется стандартизованной (по отношению к X ) или просто стандартизацией X
- 21. Ковариация X и Y Свойства: Cov(X, Y) = M(X · Y) - MX · MY Cov(X,
- 22. Коэффициент корреляции между случайными величинами:
- 24. Скачать презентацию



















 Презентация Доли. Обыкновенные дроби
Презентация Доли. Обыкновенные дроби Особенности обучения математике в малокомплектной школе
Особенности обучения математике в малокомплектной школе Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка»
Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка» Арифметикалық амалдар
Арифметикалық амалдар МАТЕМАТИКА-ЦАРИЦА НАУК? ВЫПОЛНИЛ ученик 9-го класса Муравский Владимир. Учитель: Матусова М.Н.
МАТЕМАТИКА-ЦАРИЦА НАУК? ВЫПОЛНИЛ ученик 9-го класса Муравский Владимир. Учитель: Матусова М.Н. Скалярное произведение векторов
Скалярное произведение векторов Закрепление изученного. Решение задач. 2 класс
Закрепление изученного. Решение задач. 2 класс Time quiz
Time quiz Моделирование систем. Детерминированные нелинейные модели с непрерывными переменными
Моделирование систем. Детерминированные нелинейные модели с непрерывными переменными Путешествие в страну Десятичных дробей.
Путешествие в страну Десятичных дробей. Геометрические фигуры вокруг нас
Геометрические фигуры вокруг нас Правильные многогранники
Правильные многогранники Үй тапсырмасын тексеру
Үй тапсырмасын тексеру Непрерывные функции и их свойства. Асимптоты
Непрерывные функции и их свойства. Асимптоты Лекция 04. О термине Геометрия
Лекция 04. О термине Геометрия Таблица умножения и деления на 2
Таблица умножения и деления на 2 Состав числа
Состав числа Рациональные уравнения
Рациональные уравнения Муниципальное бюджетное общеобразовательное учреждение «Гатчинская вечерняя (сменная) общеобразовательная школа» Ленинградско
Муниципальное бюджетное общеобразовательное учреждение «Гатчинская вечерняя (сменная) общеобразовательная школа» Ленинградско Нахождение дроби от числа
Нахождение дроби от числа Числовые промежутки
Числовые промежутки Математическое моделирование
Математическое моделирование Аттестационная работа. Планирование работы образовательного учреждения при обучении дисциплин естественно-математического цикл
Аттестационная работа. Планирование работы образовательного учреждения при обучении дисциплин естественно-математического цикл Цікаві задачі з математики
Цікаві задачі з математики Начальные геометрические сведения
Начальные геометрические сведения Математическая логика
Математическая логика Отношение чисел и величин. Чтение, свойства, задачи
Отношение чисел и величин. Чтение, свойства, задачи Элементы математического анализа. Введение
Элементы математического анализа. Введение