Содержание
- 2. Рассмотрим функцию Найдем Дифференциал функции
- 3. Приращение функции можно рассматривать как сумму двух слагаемых: - линейное относительно - нелинейное относительно
- 4. При оба слагаемых стремятся к нулю, но второе слагаемое быстрее стремится к нулю. Поэтому при малых
- 5. Теорема. Если функция имеет в точке дифференциал, то она имеет в этой точке производную и наоборот,
- 6. Примеры. Найти дифференциалы функций 1) 2)
- 7. Теорема. Если функция дифференцируема в точке то она в этой точке непрерывна. Связь между дифференцируемостью и
- 8. Пример. В точке функция непрерывна, так как
- 9. Справа от нуля поэтому Слева от нуля поэтому
- 10. Таким образом, отношение при справа и слева имеет различные пределы, а это значит, что при это
- 11. Схема исследования функции 1) Найти область определения функции 2) Исследовать функцию на четность и нечетность 3)
- 12. 4) Найти асимптоты кривой 5) Исследовать функцию по знаку первой производной , т.е. найти интервалы возрастания,
- 13. 6) Исследовать функцию по знаку второй производной , т.е. найти интервалы выпуклости, вогнутости, точки перегиба 7)
- 14. Пример. Исследовать функцию и построить график: 1) Область определения:
- 15. 2) Чётность, нечётность. четная, если нечетная, если функция нечетная, следовательно график функции симметричен относительно начала координат.
- 16. 3) Точки пересечения с осями координат 4) Асимптоты – это прямые, к которым стремится график функции
- 17. Асимптоты бывают: a) вертикальные. Они параллельны оси Уравнение вертикальной асимптоты b) наклонные. Уравнение где
- 18. c) если то и наклонная асимптота становится горизонтальной, т.е. параллельной оси Найдем асимптоты кривой Т.к. то
- 19. Аналогично, - вертикальная асимптота. Заметим, что кривая может иметь сколько угодно вертикальных асимптот. Пример. Вертикальные асимптоты
- 20. Найдем наклонную асимптоту
- 22. - наклонная асимптота.
- 23. Найдем
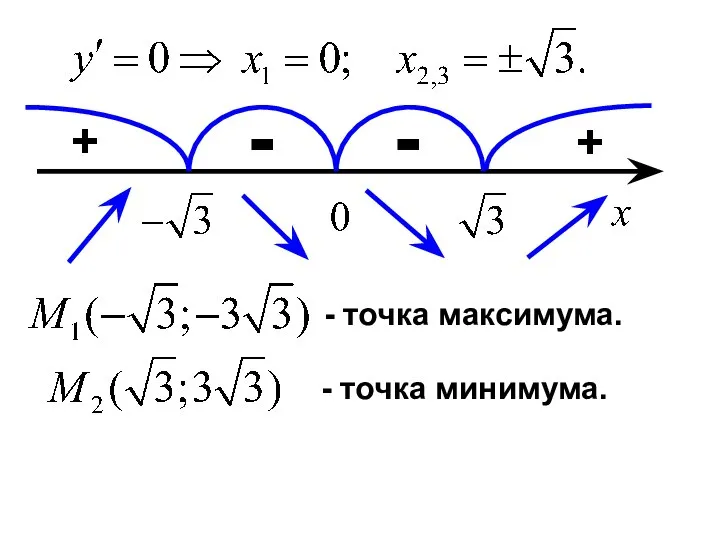
- 24. - точка максимума. - точка минимума. + - + -
- 25. Можно было не рассматривать т.е. функция нечетная и достаточно построить график только для а затем отобразить
- 26. Найдем
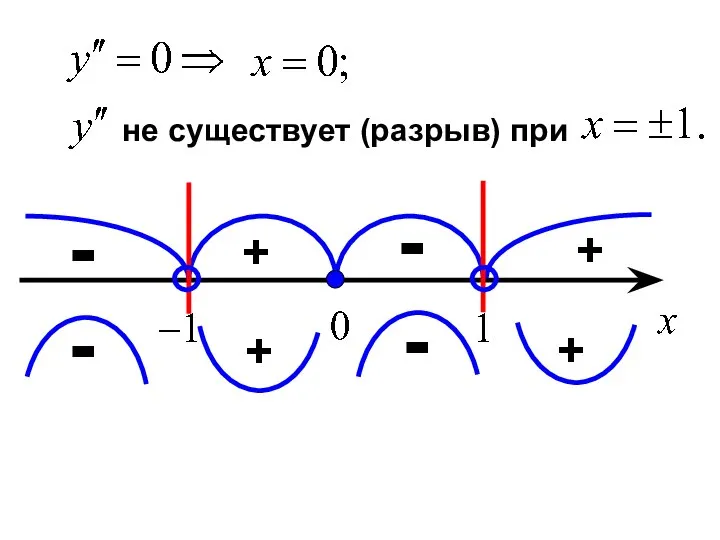
- 28. не существует (разрыв) при + - + -
- 29. Если то функция вогнута. Если то функция выпукла. + + -
- 30. Точки, в которых выпуклость меняется на вогнутость или наоборот, называются точками перегиба. 7) Для построения графика
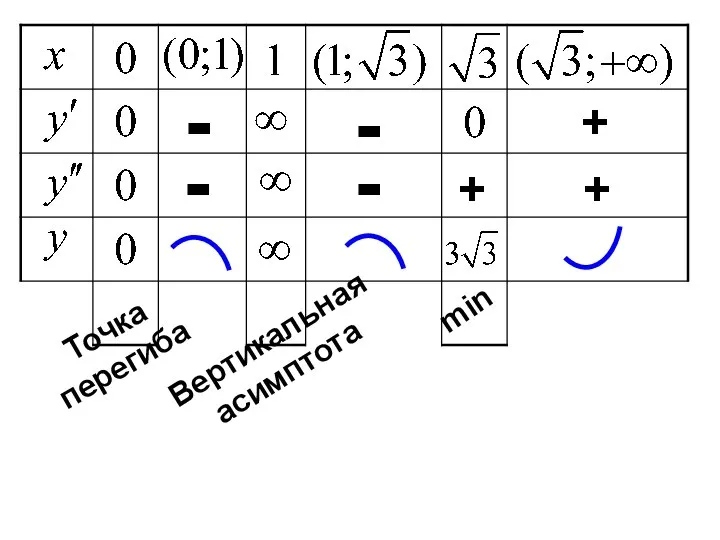
- 31. + - - - - + + Точка перегиба Вертикальная асимптота min
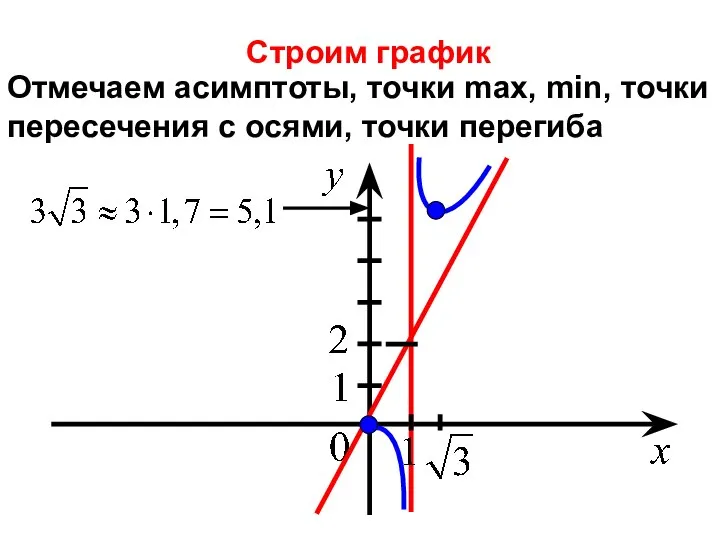
- 32. Строим график Отмечаем асимптоты, точки max, min, точки пересечения с осями, точки перегиба
- 33. Для строим график, используя нечетность функции.
- 35. Скачать презентацию







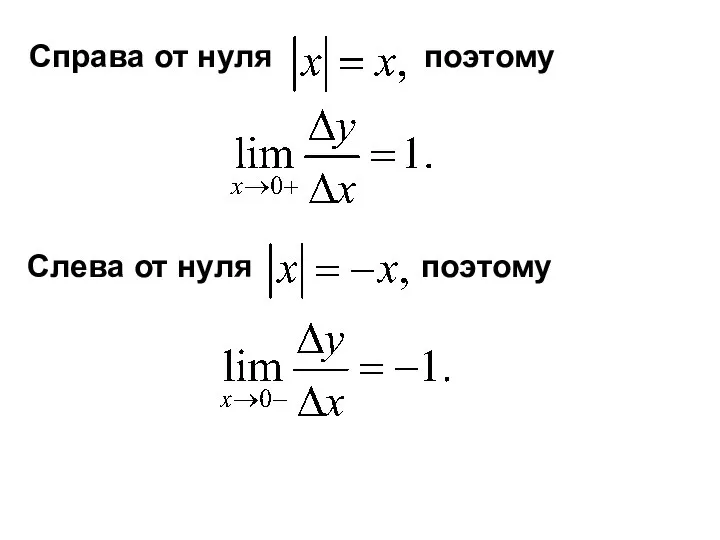











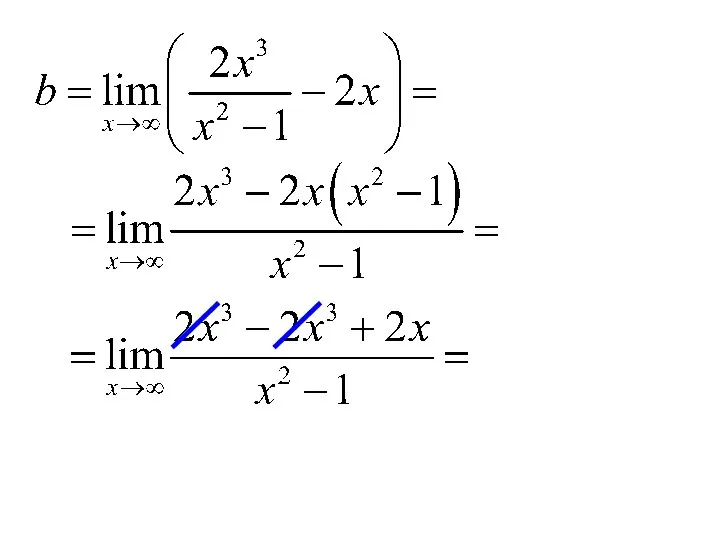

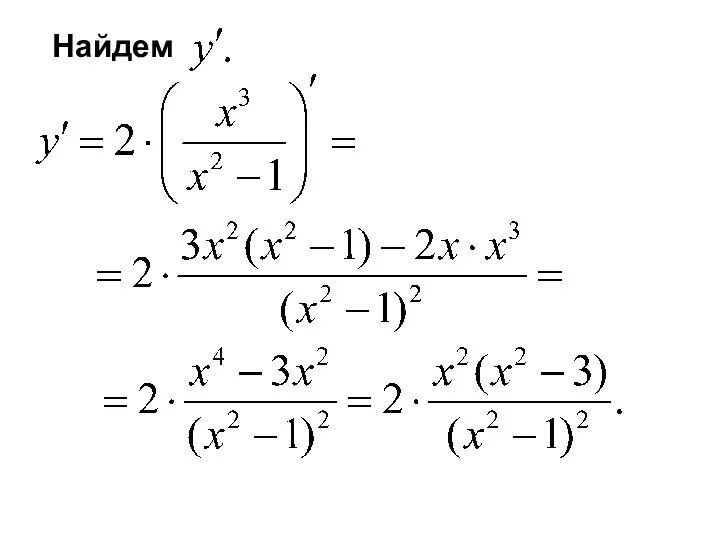

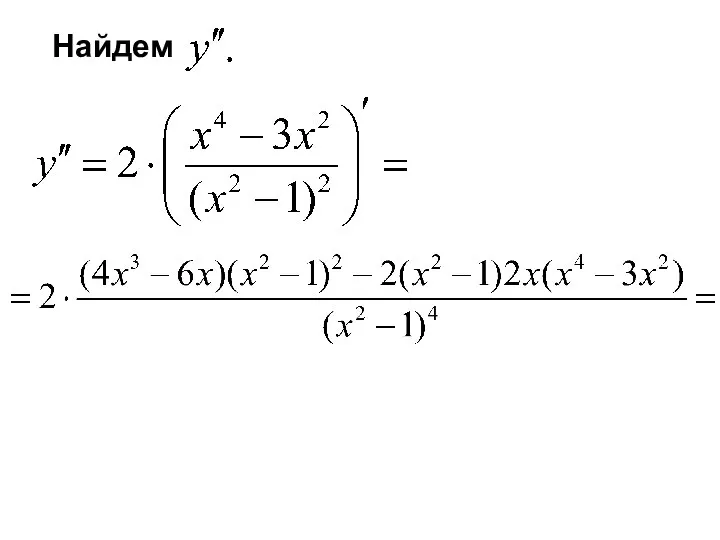
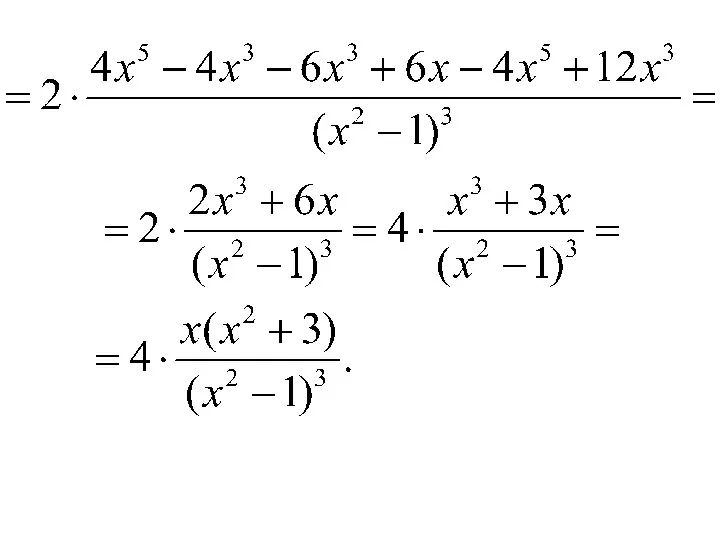



 Признаки подобия треугольников
Признаки подобия треугольников Системы линейных уравнений
Системы линейных уравнений Треугольники. Третий признак равенства
Треугольники. Третий признак равенства  Урок математики в 7 классе
Урок математики в 7 классе Дифференциальное исчисление функции нескольких действительных переменных. Тема 3.3
Дифференциальное исчисление функции нескольких действительных переменных. Тема 3.3 Пространство и время. Всеобщие формы существования материи
Пространство и время. Всеобщие формы существования материи Счет 1, 2, 3
Счет 1, 2, 3 Презентация по математике "ПОВОРОТ" - скачать бесплатно
Презентация по математике "ПОВОРОТ" - скачать бесплатно Степень с натуральным показателем
Степень с натуральным показателем Свойства логарифма и логарифмической функции. Урок обобщения и систематизации знаний
Свойства логарифма и логарифмической функции. Урок обобщения и систематизации знаний Решение задач по механике с использованием тригонометрии Для профильного физико-математического 10 класса
Решение задач по механике с использованием тригонометрии Для профильного физико-математического 10 класса Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Предел и непрерывность функции
Предел и непрерывность функции Теорема Пифагора
Теорема Пифагора Дисперсионный анализ. Основные задачи дисперсионного анализа
Дисперсионный анализ. Основные задачи дисперсионного анализа Построение графика функции у=mf(x)
Построение графика функции у=mf(x) История математики Автор: Стребкова Мария 7-а класс.
История математики Автор: Стребкова Мария 7-а класс. Древняя Греция. Числа правят миром
Древняя Греция. Числа правят миром Упрощение выражений
Упрощение выражений Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Диаграммы рассеивания
Диаграммы рассеивания Аттестационная работа. Математика вокруг нас. Числа в загадках, пословицах и поговорках. (1 класс)
Аттестационная работа. Математика вокруг нас. Числа в загадках, пословицах и поговорках. (1 класс) Обыкновенные дроби. 5 класс
Обыкновенные дроби. 5 класс Элементы теории вероятностей
Элементы теории вероятностей Уравнения и неравенства с двумя переменными
Уравнения и неравенства с двумя переменными Решение неравенств, содержащих переменную под знаком модуля
Решение неравенств, содержащих переменную под знаком модуля Геометрические иллюзии, или всегда ли мы видим то, что видим
Геометрические иллюзии, или всегда ли мы видим то, что видим Тригонометрия. Таблица значений тригонометрических функций
Тригонометрия. Таблица значений тригонометрических функций