Дифференциальное исчисление функций нескольких переменных

Функция n переменных

Переменная u называется функцией n переменных (аргументов) x,y,z,…,t, если

Функция двух переменных

Функцией двух переменных называется закон, по которому каждой паре

Частные производные первого порядка

Частной производной от функции z =f(x,y) по независимой

Полный дифференциал

Полный дифференциал функции z =f(x,y) вычисляется по формуле
Полный дифференциал

Частные производные высших порядков

Частными производными второго порядка от функции z =f(x,y)

Дифференциалы высших порядков

Дифференциалом второго порядка от функции z=f(x,y) называется дифференциал от

Дифференцирование сложных функций

Пусть z=f(x,y), где х=φ(t), у=ψ(t) и функции f(x,y), φ(t),

Дифференцирование неявных функций

Производные неявной функции двух переменных z=f(x,y), заданной с помощью

Экстремум функции

Функции z=f(x,y) имеет максимум (минимум) в точке M0(x0;y0) если

Пусть M0(x0;y0) - стационарная точка функции z=f(x,y). Обозначим
И составим дискриминант Δ=AC-B2.

Неопределённый интеграл

Первообразная функция

Функция F(x) называется первообразной для функции f(x) на интервале X=(a,b),

Неопределённый интеграл

Множество всех первообразных функции F(x)+С для f(x) называется неопределённым интегралом

Свойства неопределённого интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а

3. Постоянный множитель можно вынести за знак интеграла:
4. Неопределенный интеграл от

Таблица неопределённых интегралов

Основные методы интегрирования

Метод интегрирования, при котором данный интеграл путем тождественных преобразований

При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала

Замена переменной в неопределённом интеграле (интегрирование подстановкой)

Метод интегрирования подстановкой заключается во

Интегрирование по частям

Формула интегрирования по частям
Формула дает возможность свести вычисление интеграла

Интегрирование рациональных дробей

Рациональной дробью называется дробь вида P(x)/Q(x), где P(x) и

Найдем интегралы от простейших дробей

Первый интеграл простейшей дроби IV типа в правой части равенства легко

Интегрирование рациональных дробей с помощью разложения на простейшие дроби

Перед интегрированием рациональной

3) Правильную рациональную дробь разложить на простейшие дроби:
4) Вычислить неопределенные коэффициенты

Интегрирование простейших иррациональных функций

Интегралы вида
где R – рациональная функция; m1,n1,m2,n2,…- целые

3. Интеграл вида
Для нахождения этого интеграла выделим в числителе производную

4.Интегралы вида
С помощью подстановки х-α=1/t этот интеграл приводится к рассмотренному п.2
5.

6. Интегралы от дифференциальных биномов
где m, n, p – рациональные

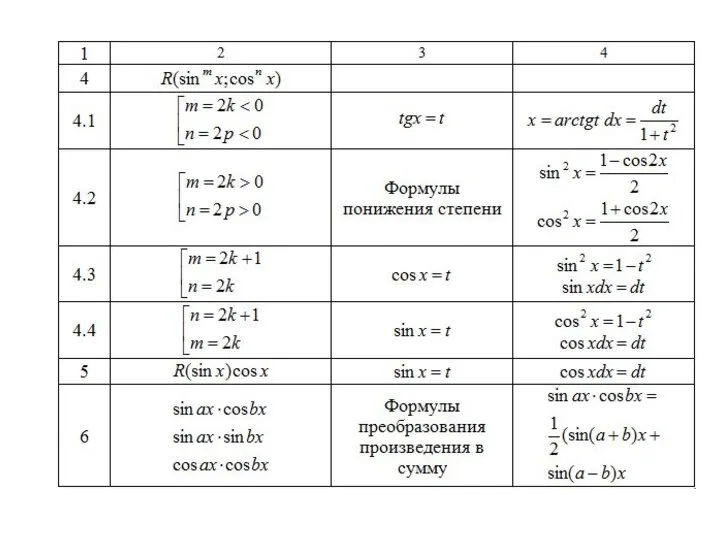
Интегрирование тригонометрических функций

Интегралы вида
где R – рациональная функция.
Под знаком интеграла находится

Определенный интеграл

Определенным интегралом от функции f(x) на отрезке [a;b] называется предел интегральных

Если f(x)>0 на отрезке [a;b], то определенный интеграл геометрически представляет собой

Свойства определенного интеграла

Правила вычисления определенных интегралов

Формула Ньютона-Лейбница:
где F(x) – первообразная для f(x), т.е.

3. Замена переменной
где х=φ(t) – функция, непрерывная вместе со своей производной

Несобственные интегралы

Несобственными интегралами называются:
1) интегралы с бесконечными пределами;
2) интегралы от

При исследовании сходимости несобственных интегралов пользуются одним из признаков сравнения.
1. Если

Вычисление площади плоской фигуры

Площадь криволинейной трапеции, ограниченной кривой у=f(x) [f(x)≥0], прямыми

Вычисление длины дуги плоской кривой

Если кривая у=f(x) на отрезке [a;b] –

Вычисление объема тела

1. Вычисление объема тела по известным площадям поперечных сечений.

Вычисление площади поверхности вращения

Если дуга гладкой кривая у=f(x) (a≤х≤b) вращается вокруг

Обыкновенные дифференциальные уравнения

Основные понятия

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и

Уравнение первого порядка

Функциональное уравнение F(x,y,y′) = 0 или y′= f(x,y), связывающее

Общее решение дифференциального уравнения 1-го порядка

Общим решением дифференциального уравнения первого порядка

Уравнение, разрешенное относительно производной

Если уравнение 1-го порядка разрешить относительно производной, то

Постановка задачи Коши

Задача отыскания решения дифференциального уравнения , удовлетворяющего начальному условию

Уравнение с разделяющимися переменными

Дифференциальное уравнение
называется уравнением с разделенными переменными.

Однородные уравнения

Дифференциальное уравнение первого
порядка называется однородным, если его

Линейные уравнения 1-го порядка

Дифференциальное уравнение первого порядка называется линейным, если

Уравнение Бернулли

Уравнением Бернулли называется уравнение 1-го порядка, имеющее вид
,

Дифференциальные уравнения 2-го порядка

Уравнение 2-го порядка имеет вид
Или
Общим решением

Задача Коши для уравнения 2-го порядка

Если уравнение 2-го порядка разрешить

Теорема существования и единственности решения уравнения 2-го порядка

Если в уравнении

Уравнения 2-го порядка, допускающие понижение порядка

Простейшее уравнение 2-го порядка

Линейные однородные уравнения

Линейным однородным дифференциальным уравнением второго порядка называется уравнение

Свойства решений линейного однородного уравнения

Теорема 1. Если у(х) является

Свойства решений линейного однородного уравнения

Теорема 2. Если и -решения уравнения,

Линейно зависимые и линейно независимые функции

Две функции и называются линейно

Если таких чисел подобрать нельзя, то функции и называются линейно

Теорема о структуре общего решения линейного однородного уравнения 2-го порядка

Если