Содержание
- 2. Пусть y = f(x) определена и непрерывна в точке Если полное приращение функции в этой точке
- 3. Необходимое и достаточное условие дифференцируемости функции Для того, чтобы функция была дифференцируемой необходимо и достаточно, чтобы
- 4. Достаточность. По условию существует производная Тогда и Приращение функции записано в таком виде, следовательно, функция дифференцируема.
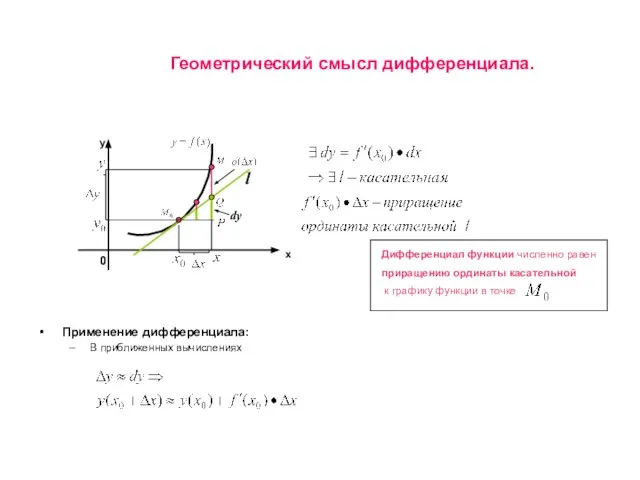
- 5. Геометрический смысл дифференциала. Применение дифференциала: В приближенных вычислениях 0 х y l dy Дифференциал функции численно
- 6. Свойства дифференциала. Пусть функции дифференцируемые. Тогда: 1. 2. 3. 4. Инвариантность формы дифференциала. Пусть функция дифференцируемая;
- 7. Таблица дифференциалов основных элементарных функций. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.
- 8. Функции двух переменных Функцией двух переменных называется закон, по которому каждой паре значений независимых переменных (аргументов)
- 9. Данную функцию обозначают следующим образом: Z = f(x; y) Поскольку упорядоченная пара значений «икс» и «игрек»
- 10. Область определения Областью определения функции двух переменных называется множество всех пар (x;y), для которых существует значение
- 11. Пример Найти область определения функции Решение: подкоренное выражение должно быть неотрицательным: и знаменатель не может равняться
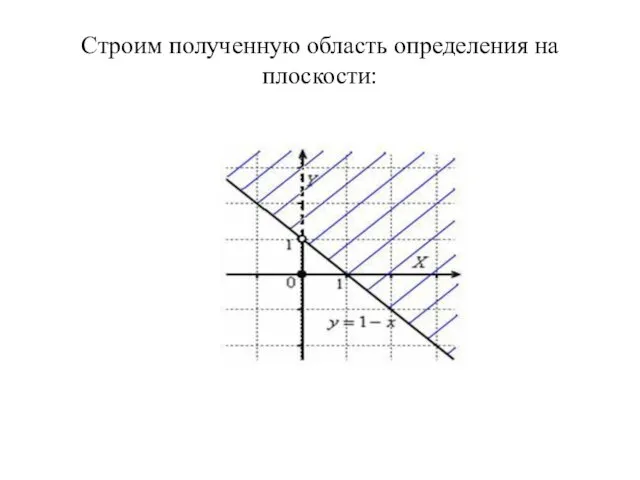
- 12. Построение области определения Строим прямую x + y - 1 = 0 и определяем полуплоскость, которая
- 13. Строим полученную область определения на плоскости:
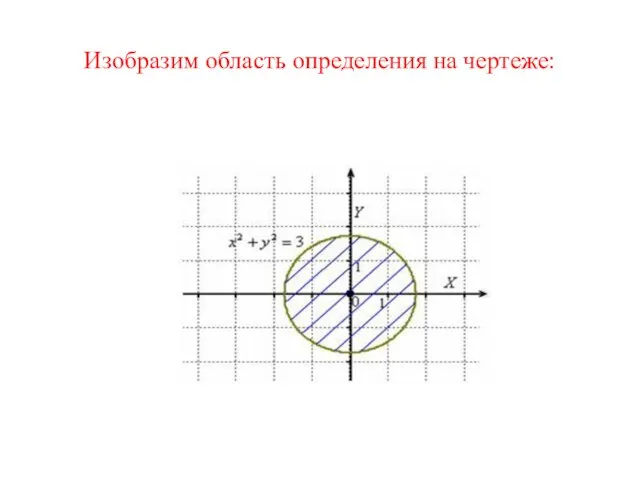
- 14. Пример Найти область определения функции Решение: Подкоренное выражение должно быть неотрицательным: или Это круг радиуса с
- 15. Изобразим область определения на чертеже:
- 17. Имеем дело с областями , ограниченными линиями. Линия, ограничивающая данную область, называется границей области. Точки области,
- 18. Если же к области относятся и точки границы, то область называется замкнутой. Связной называется область, любые
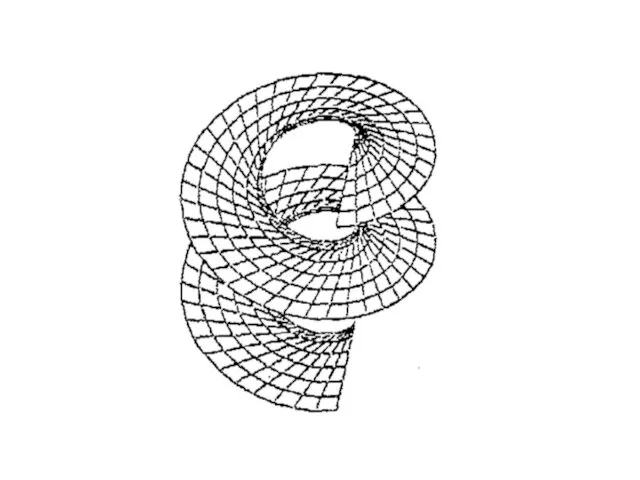
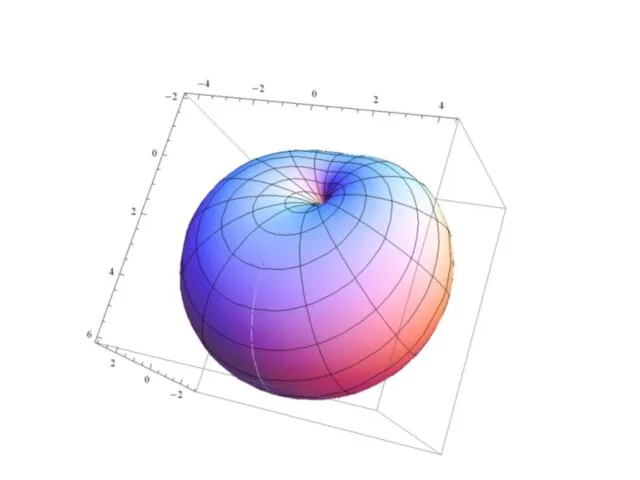
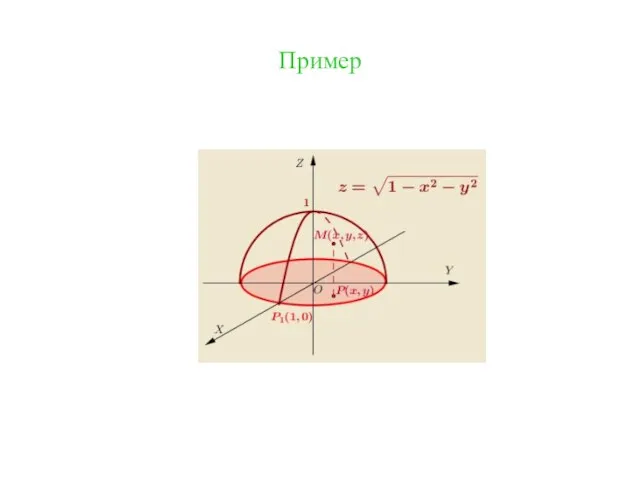
- 19. Геометрическое изображение функции двух переменных. Графиком функции z = f(x; y) является поверхность с уравнением z
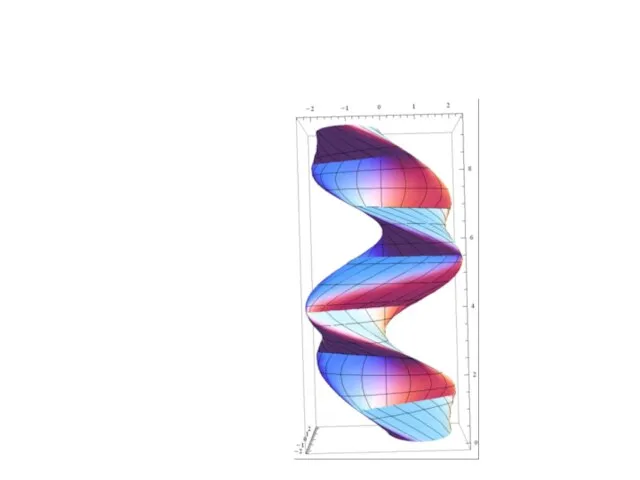
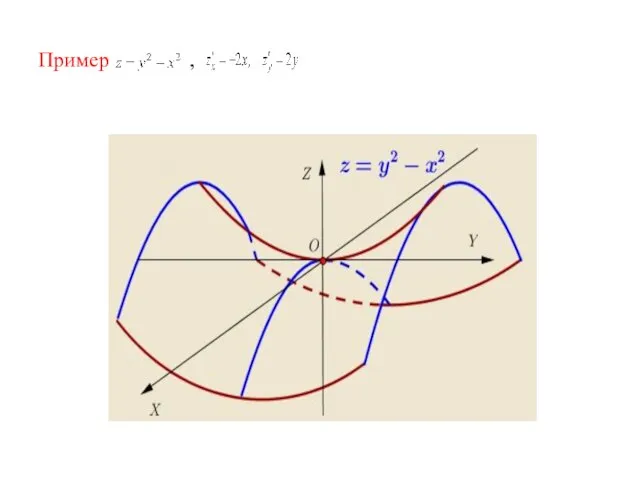
- 30. Пример
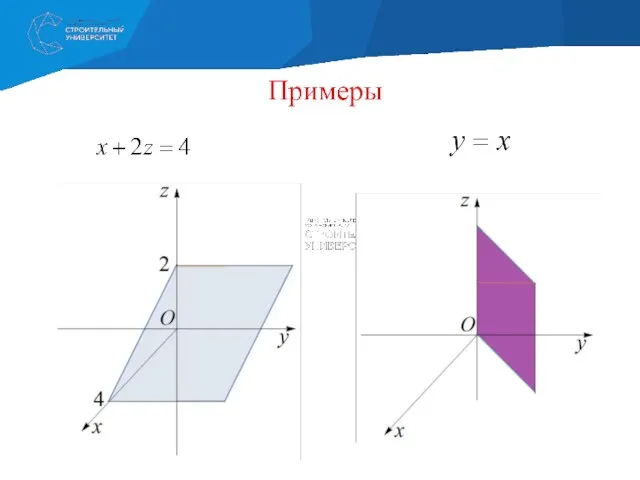
- 32. Построить самостоятельно: Плоскость: z = 1 – x Полусфера:
- 33. Ограниченность функции двух переменных Функция z = f(x;y) называется ограниченной в области D, если существуют такие
- 36. Частные приращения функции двух переменных Частным приращением по x функции z = f(x; y) в точке
- 37. Частным приращением по y функции z = f(x; y) в точке называется разность , то есть
- 38. Полное приращение функции z = f(x;y) Полным приращением функции z = f(x;y) в точке называется разность
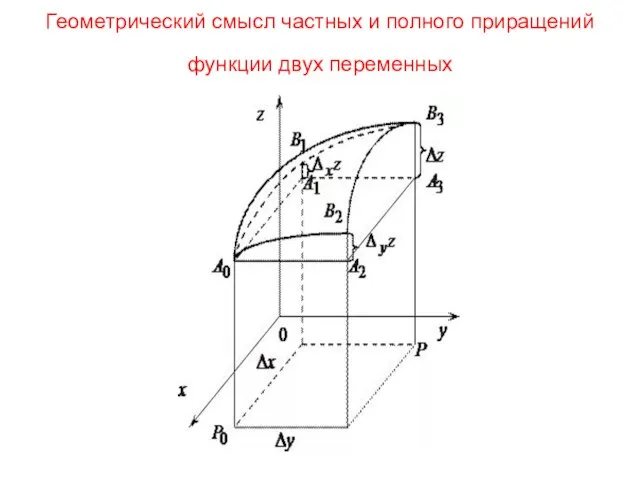
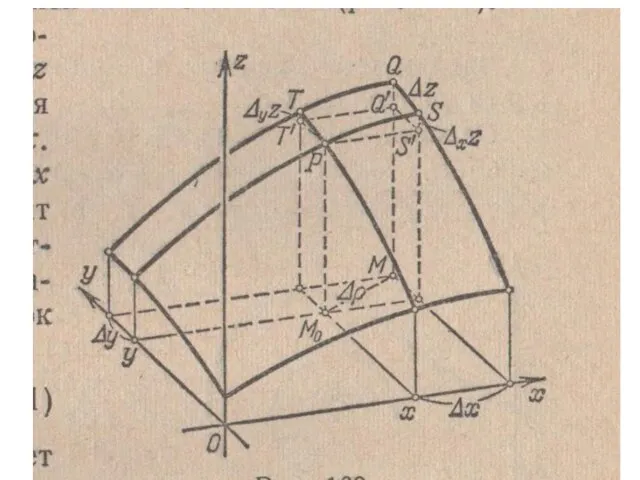
- 39. Геометрический смысл частных и полного приращений функции двух переменных
- 41. Непрерывность функции в точке. Функция называется непрерывной в точке , если 1). функция определена в точке
- 42. Второе определение непрерывности функции z =f(x; y) в точке Пусть функция z = f(x; y) непрерывна
- 44. Частные производные функции двух переменных z = f (x; y) Частной производной функции z = f(x;
- 45. Пример Найти частные производные: (y = const) (x = const)
- 46. Пример Найти частные производные: (y = const) (x = const)
- 47. Геометрический смысл частных производных Пусть . Это плоскость, параллельная координатной плоскости Oxz. В пересечении с поверхностью
- 48. Аналогично, Пусть . Это плоскость, параллельная координатной плоскости Oyz. В пересечении с поверхностью z = f(x;
- 50. Физический смысл частных производных Частная производная - это скорость изменения z относительно переменной x в точке
- 53. Или: функция называется дифференцируемой в точке, если ее полное приращение можно представить в виде , где
- 54. Полный дифференциал: Что представляют собой A и B ?
- 55. Связь между дифференцируемостью и существованием частных производных функции двух переменных Если функция z = f(x; y)
- 56. Доказательство Дадим приращение величине x, а y оставляем постоянным , Тогда , , так как .
- 58. Теорема Если в точке (x; y) частные производные существуют и непрерывны, то в этой точке функция
- 59. Теорема. Связь между дифференцируемостью и непрерывностью функции в точке. Если функция z = f(x; y) дифференцируема
- 60. Частные производные высших порядков Частными производными второго порядка функции z = f (x,y) называются частные производные
- 61. Теорема Пусть функция z = f(x; y) в некоторой окрестности точки (x; y) имеет смешанные производные
- 62. Пример Найти частные производные второго порядка
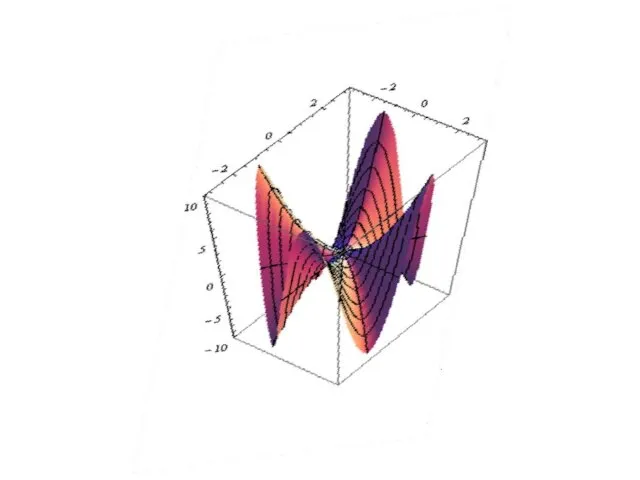
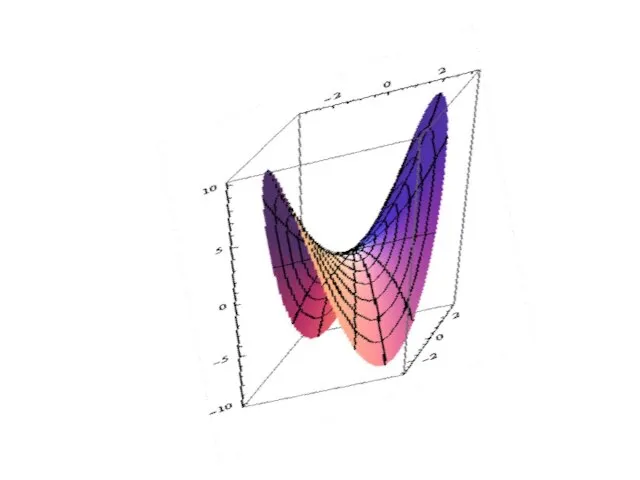
- 64. Геометрическое изображение точек экстремума:
- 66. Пример ,
- 69. Скачать презентацию





















































 Треугольники, 7 класс
Треугольники, 7 класс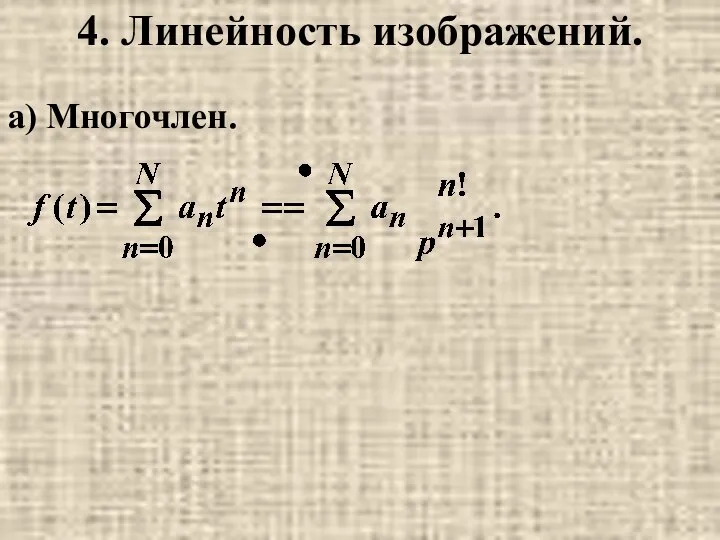 Линейность изображений
Линейность изображений Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs
Chapter 3. Polynomial and Rational Functions. 3.2 Polynomial Functions and Their Graphs Признаки делимости на 10, на 5, на 2
Признаки делимости на 10, на 5, на 2 Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»  Текстовые задачи на движение
Текстовые задачи на движение Тела вращения. Цилиндр. Сечение. Вписанная и описанная призма. Конус. Сечение. Вписанная и описанная пирамида. Шар. Симметрия
Тела вращения. Цилиндр. Сечение. Вписанная и описанная призма. Конус. Сечение. Вписанная и описанная пирамида. Шар. Симметрия Нахождение процентов от числа и числа по его проценту. 5 класс
Нахождение процентов от числа и числа по его проценту. 5 класс Точка, линия, прямая и кривая линии. Число 2. Цифра 2
Точка, линия, прямая и кривая линии. Число 2. Цифра 2 Следствия из аксиом I - III
Следствия из аксиом I - III Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода
Признаки сходимости несобственных интегралов. Теорема 1. Признак сравнения несобственных интегралов 1 рода Условная вероятность
Условная вероятность Подготовка к введению задач в 2 действия
Подготовка к введению задач в 2 действия Делимость натуральных чисел
Делимость натуральных чисел Лента Мебиуса. Все гениальное просто. (приложение)
Лента Мебиуса. Все гениальное просто. (приложение)  Подготовка к ГИА. Нахождение знаков коэффициентов квадратичной функции по графику
Подготовка к ГИА. Нахождение знаков коэффициентов квадратичной функции по графику 20161216_den_fibonachchi
20161216_den_fibonachchi Симметрические многочлены
Симметрические многочлены Три признака параллельности двух прямых
Три признака параллельности двух прямых Решение практико-ориентированных задач ЕГЭ
Решение практико-ориентированных задач ЕГЭ Пересекающиеся прямые. Вертикальные и смежные углы
Пересекающиеся прямые. Вертикальные и смежные углы Полуправильные многоугольники. Длина и площадь
Полуправильные многоугольники. Длина и площадь Криволинейные интегралы 2 рода
Криволинейные интегралы 2 рода Натуральные числа. Обобщающий урок
Натуральные числа. Обобщающий урок Логико-когнетивные основы урока алгебры
Логико-когнетивные основы урока алгебры Определение угла. Развернутый угол
Определение угла. Развернутый угол Інтегральне числення
Інтегральне числення Решение заданий ЕГЭ. Урок-консультация. 11 класс
Решение заданий ЕГЭ. Урок-консультация. 11 класс