Элементы теории множеств

Можно ли дать определение понятию «Множество»?

Множество – одно из фундаментальных первичных

Множества принято обозначать заглавными латинскими буквами (А,B,…)
Объекты, которые образуют множество, называют

Примеры множеств:

множество учащихся в данной аудитории;
множество людей, живущих на нашей планете

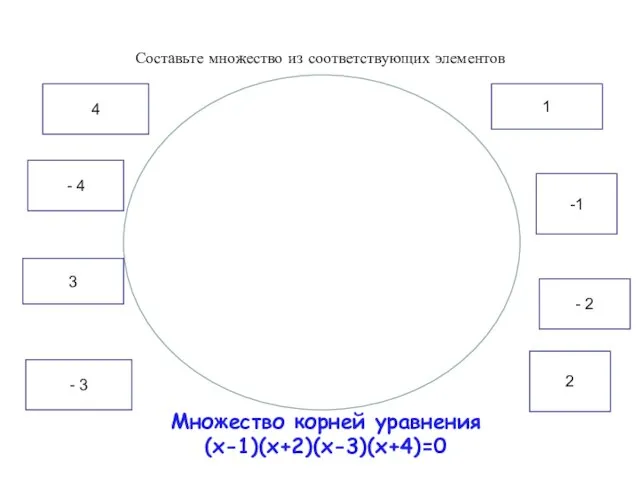
Множество корней уравнения (x-1)(x+2)(x-3)(x+4)=0

Составьте множество из соответствующих элементов

4

- 4

3

1

-1

- 2

- 3

2

Принадлежность элемента множеству

Если элемент x принадлежит множеству X, то записывают x

Подмножество

Говорят, что множество А содержится в множестве В или  множество

Способы задания множеств

Множество может быть задано перечислением всех его элементов

Например, перечислением заданы следующие множества:

А={1,2,3,5,7} — множество чисел
Х={x1,x2,...,xn} —

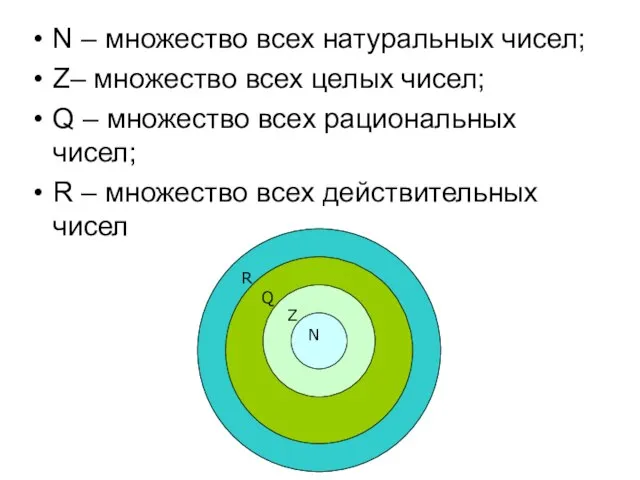
N – множество всех натуральных чисел;
Z– множество всех целых чисел;
Q –

Задайте перечислением элементов множество:

1) A = {x / x ∈ N,

По числу элементов, входящих в множество, множества делятся на три класса:

1

Множество является КОНЕЧНЫМ, если оно состоит из конечного числа элементов

Пример
Множество

Множество является БЕСКОНЕЧНЫМ, если оно состоит из бесконечного числа элементов

Пример
Множество

Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается

Мощность множества

Число элементов конечного множества называют мощностью этого множества и обозначают

УНИВЕРСАЛЬНОЕ МНОЖЕСТВО

В любой конкретной задаче приходится иметь дело с подмножествами некоторого,

Наглядное представление множеств

Наглядно свойства множеств, операции над множествами и отношения между

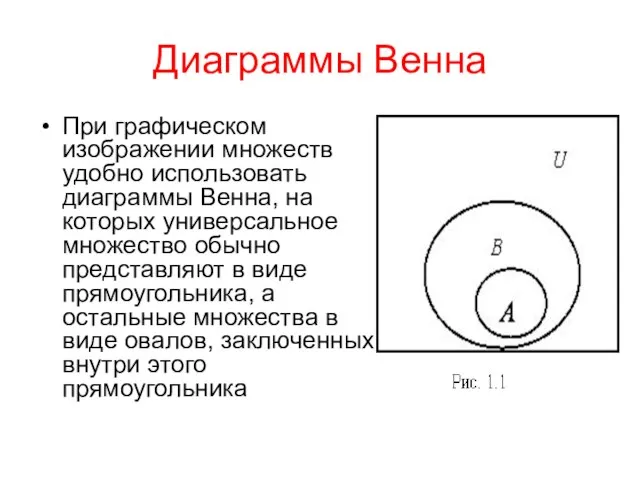
Диаграммы Венна

При графическом изображении множеств удобно использовать диаграммы Венна, на которых

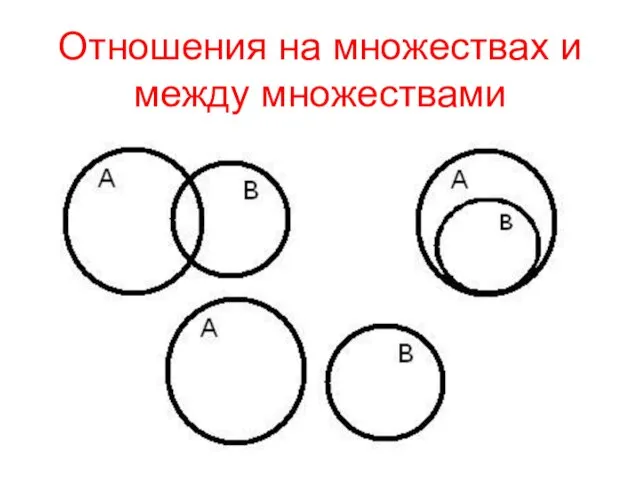
Отношения на множествах и между множествами

БИНАРНЫЕ ОТНОШЕНИЯ

Отношения между парами объектов называются бинарными.
Примеры:
Равенство
Неравенство
Принадлежности
Включения
«Быть братом», делиться на

ОТНОШЕНИЕ РАВЕНСТВА

Два множества А и В называются  равными ( А =

ОТНОШЕНИЕ ВКЛЮЧЕНИЯ

Если множество А  является подмножеством множества  В (А ⊂

Определить как между собой соотносятся множества A = {1, 2, 3,

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

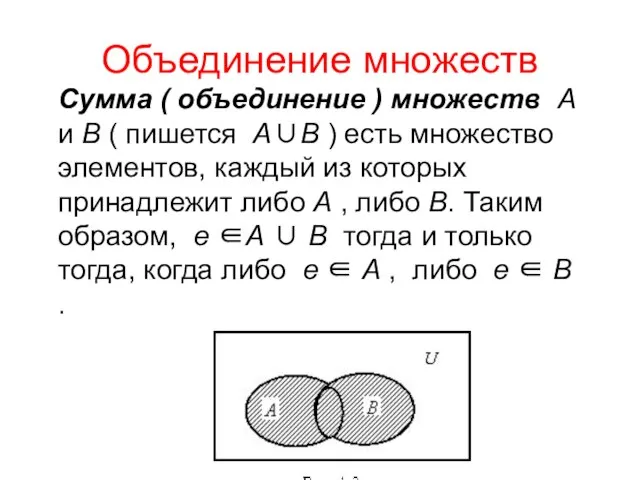
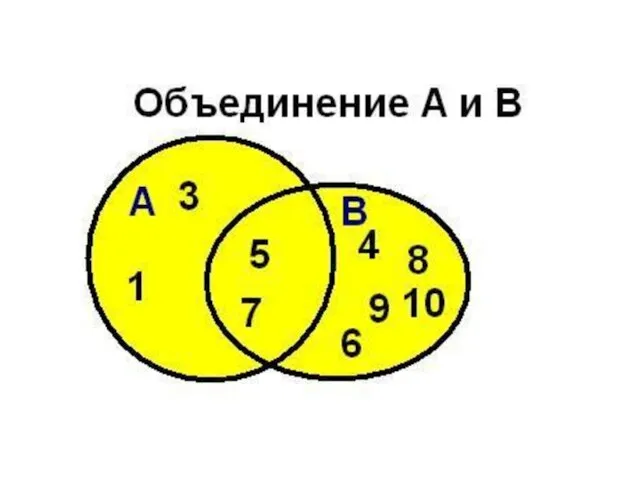
Объединение множеств

Сумма ( объединение ) множеств  А и В ( пишется 

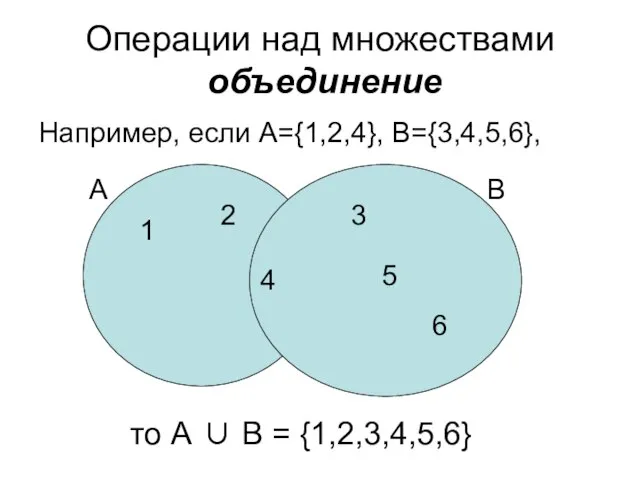
Операции над множествами объединение

Например, если А={1,2,4}, B={3,4,5,6},

то А ∪ B

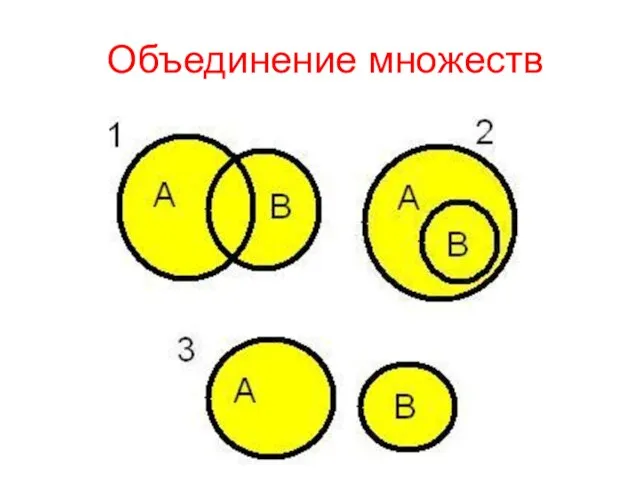
Объединение множеств

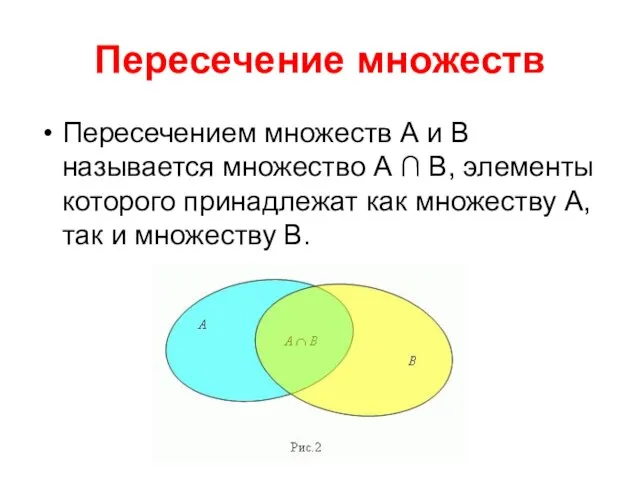
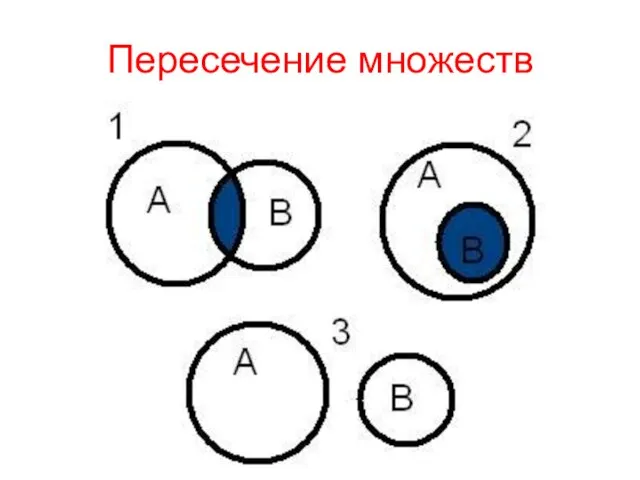
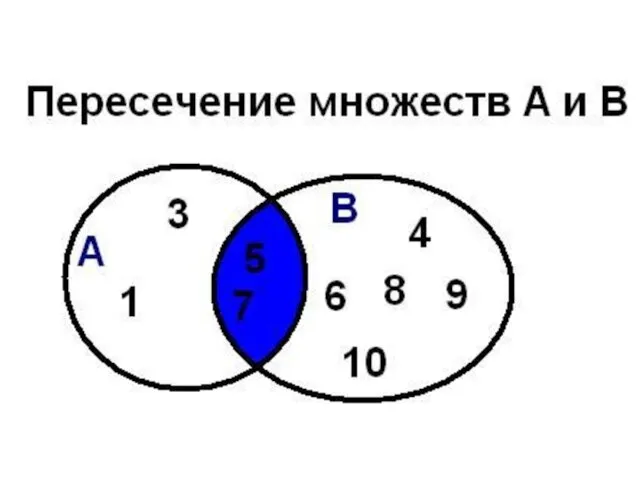
Пересечение множеств

Пересечением множеств А и В называется множество А ∩ В,

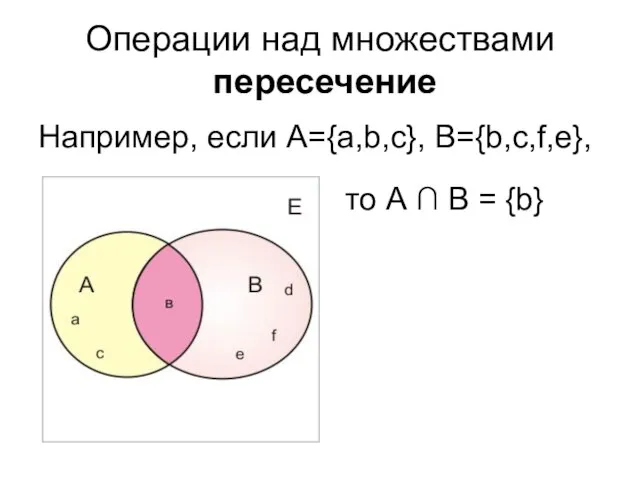
Операции над множествами пересечение

Например, если А={a,b,c}, B={b,c,f,e},

то А ∩ В

Пересечение множеств 

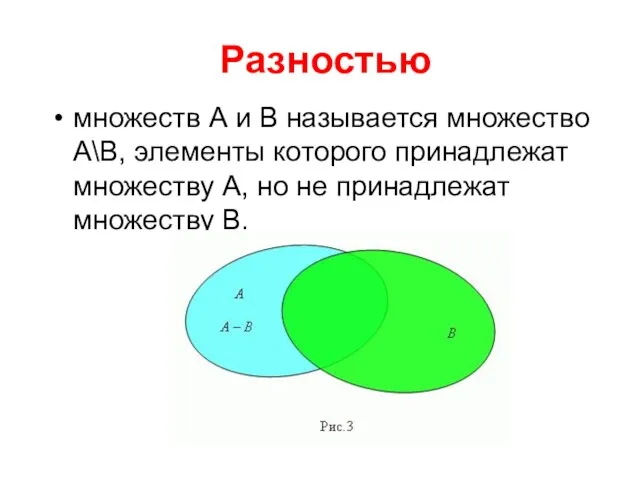
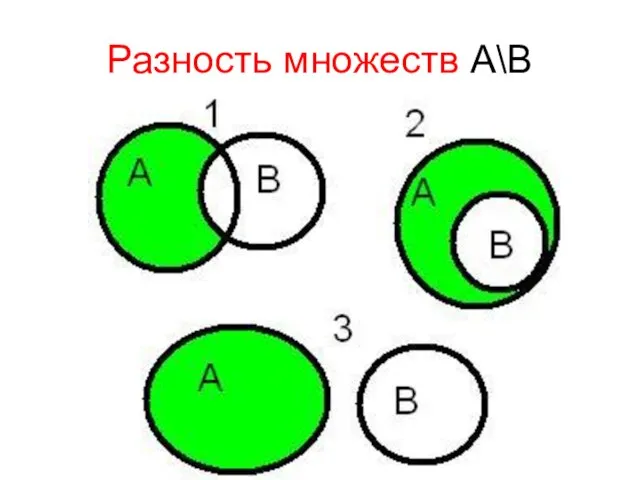
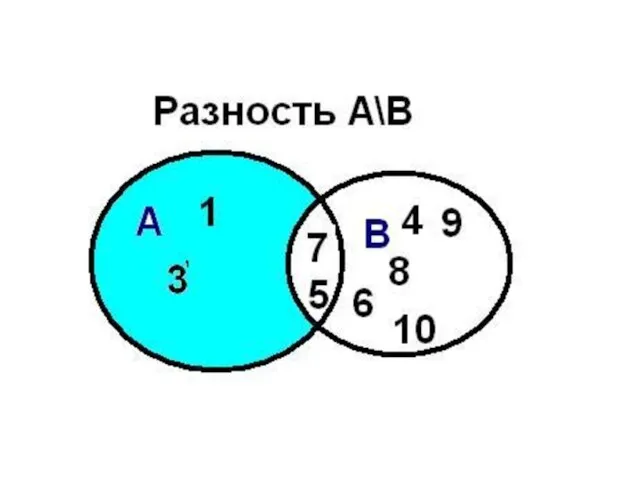
Разностью

множеств А и В называется множество А\В, элементы которого принадлежат

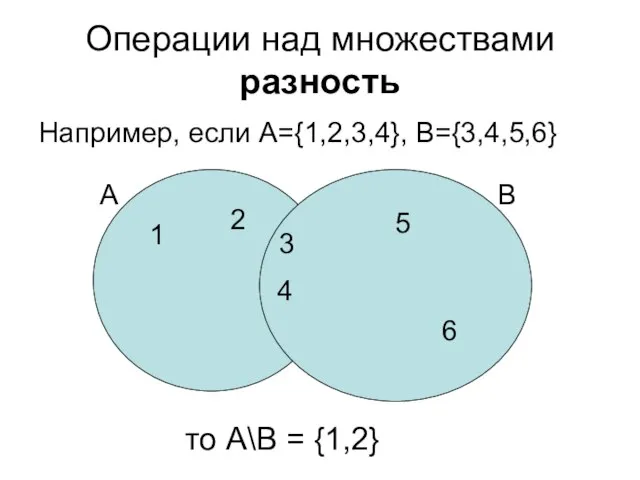
Операции над множествами разность

Например, если А={1,2,3,4}, B={3,4,5,6}

то А\В = {1,2}

1

2

4

А

4

3

5

6

В

Разность множеств А\В

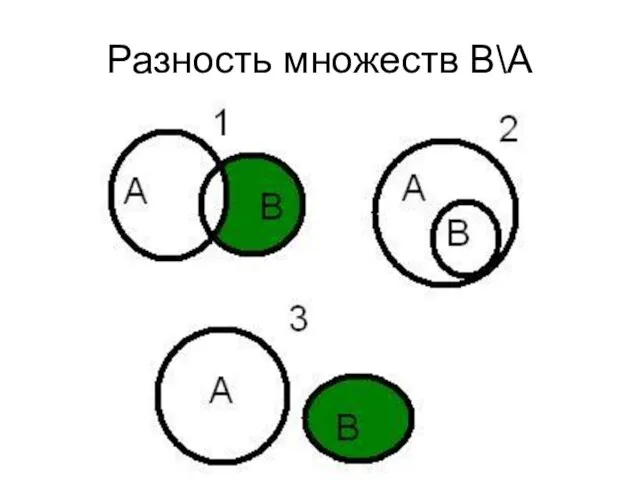
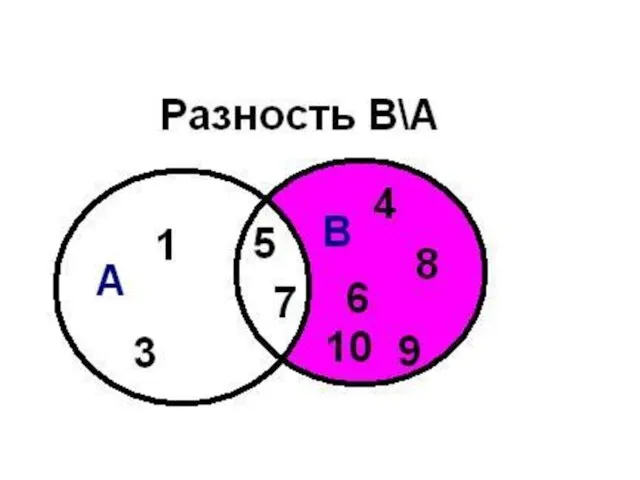
Разность множеств В\А

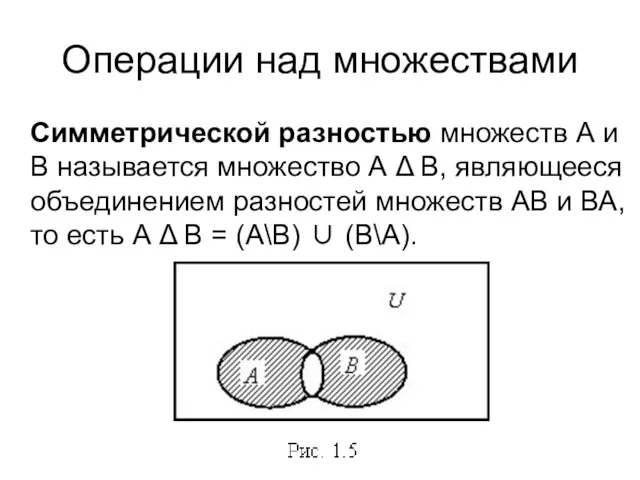
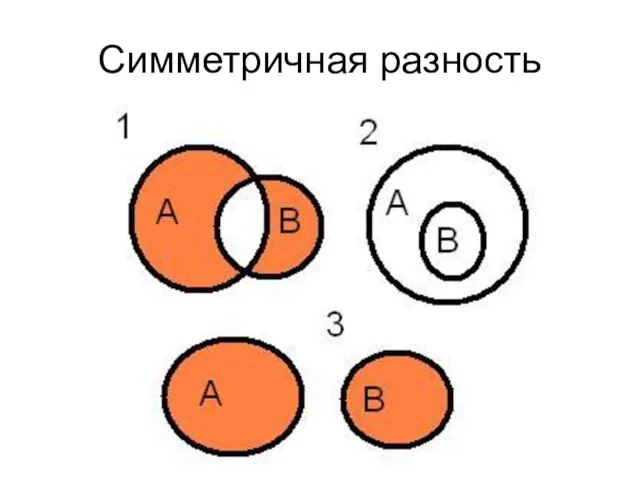
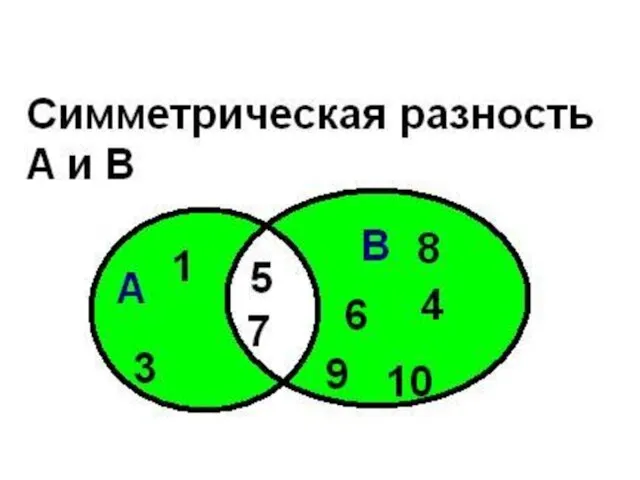
Операции над множествами

Симметрической разностью множеств А и В называется множество А

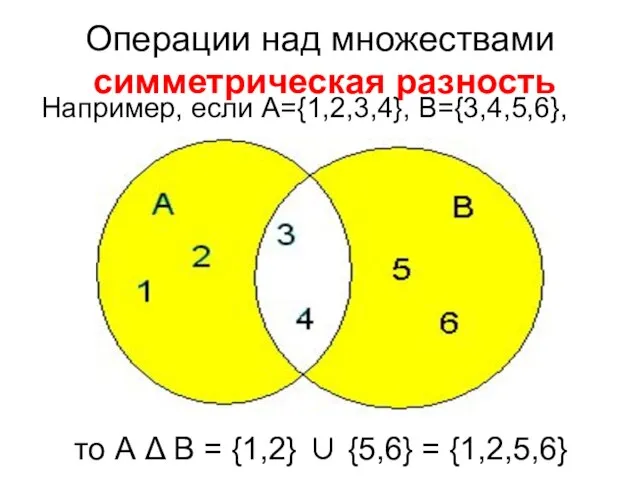
Операции над множествами симметрическая разность

Например, если А={1,2,3,4}, B={3,4,5,6},

то А

Симметричная разность

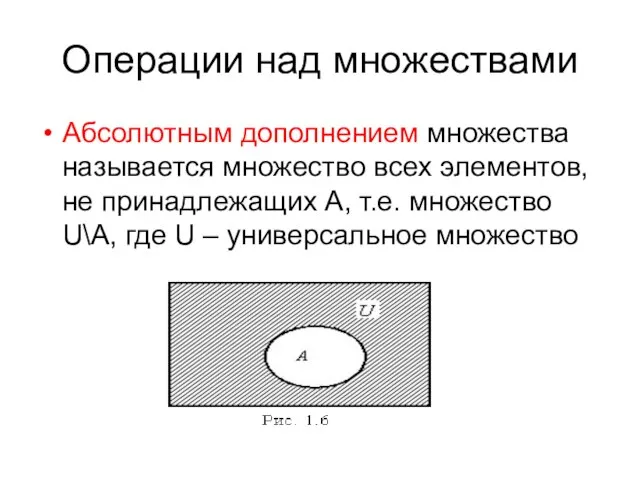
Операции над множествами

Абсолютным дополнением множества называется множество всех элементов, не принадлежащих

Свойства операций над множествами:

П р и м е р ы

 Множество детей является подмножеством всего

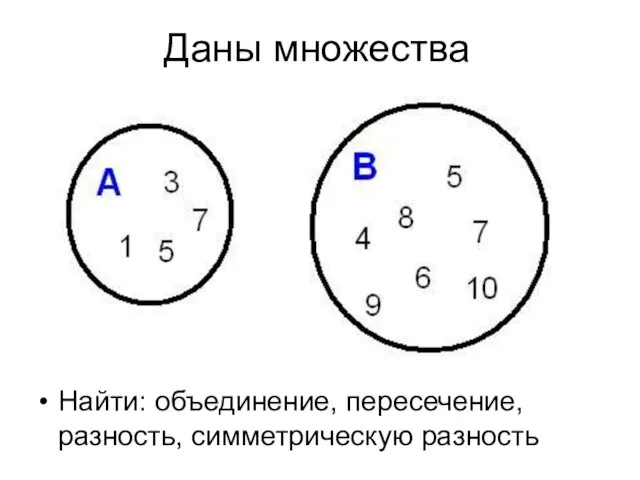
Даны множества

Найти: объединение, пересечение, разность, симметрическую разность

Формула мощности объединения непересекающихся конечных множеств (1)

Если конечное множество А представимо

Формула включений и исключений для двух множеств (2)

Для любых двух

Формула включений и исключений для трех множеств (2)

Для любых трех

Задача

На вступительном экзамене по математике были предложены три задачи: по алгебре,