Содержание
- 2. Случайные сигналы в ОЭС Случайность появляется всегда для систем с бесконечным числом свободы – атомарное строение
- 3. Задачи с равновероятными исходами Системы с бесконечным числом исходов Основные понятия теории вероятности – анализ азартных
- 4. Геометрическая вероятность Что такое предел экспериментальной величины с точки зрения математической теории? Hall A. On an
- 5. Вероятностное пространство Хорошо для математики, но неясна связь с физикой - частотой события Задано пространство Ω
- 6. Случайная величина что позволяет не разделять непрерывную и дискретную случайные величины Случайная величина: функция ξ= ξ(ω),
- 7. Моменты случайной величины Моменты позволяют оценить не саму величину, а ее распределение Центральные моменты случайной величины:
- 8. Неравенство Чебышева Экспериментальное определение (измерение) математического ожидания
- 9. Закон больших чисел в форме Bernoulli Закон больших чисел является мостиком, соединяющим математическую теорию с физическим
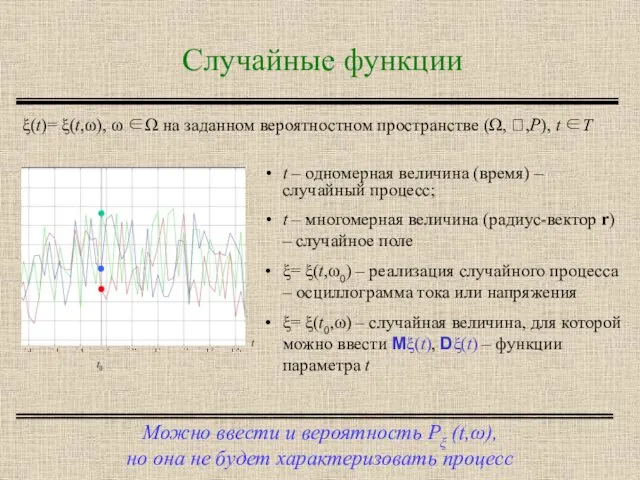
- 10. Случайные функции Можно ввести и вероятность Pξ (t,ω), но она не будет характеризовать процесс ξ(t)= ξ(t,ω),
- 12. Скачать презентацию








 Властивості степенів. Розв язування вправ. 7 клас
Властивості степенів. Розв язування вправ. 7 клас Понятие логарифма, основные свойства логарифмов
Понятие логарифма, основные свойства логарифмов Решение задач с помощью систем уравнений второй степени
Решение задач с помощью систем уравнений второй степени «Нет» и «не» в этикете (занятие-игра) Автор: Ефименко Мария Витальевна, учитель математики, классный руководитель 7 класса. МБОУ
«Нет» и «не» в этикете (занятие-игра) Автор: Ефименко Мария Витальевна, учитель математики, классный руководитель 7 класса. МБОУ  УМК « Планета знаний» урок математики в 4 классе
УМК « Планета знаний» урок математики в 4 классе Алгебра және анализ бастамалары пәні. 10 сынып
Алгебра және анализ бастамалары пәні. 10 сынып Волшебная страна - геометрия
Волшебная страна - геометрия Десятичные дроби и действия над ними
Десятичные дроби и действия над ними  Координаты вектора
Координаты вектора Правильные многоугольники
Правильные многоугольники Старинные русские меры длины Автор презентации: Хохлова Ольга
Старинные русские меры длины Автор презентации: Хохлова Ольга Презентация по математике "ЗАЧЕМ НУЖНА МАТЕМАТИКА" - скачать бесплатно
Презентация по математике "ЗАЧЕМ НУЖНА МАТЕМАТИКА" - скачать бесплатно Деление с остатком
Деление с остатком Статистические методы анализа данных параметров транспортного процесса
Статистические методы анализа данных параметров транспортного процесса Окружность. Отличие круга от окружности
Окружность. Отличие круга от окружности Простейшие задачи в координатах (9 класс)
Простейшие задачи в координатах (9 класс) Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Динамические системы и их математические модели
Динамические системы и их математические модели Корреляция. Методы исследования
Корреляция. Методы исследования Математическое путешествие
Математическое путешествие Определение арксинуса, арккосинуса числа а
Определение арксинуса, арккосинуса числа а Часы. Определяем время
Часы. Определяем время Угол между векторами. Скалярное произведение векторов
Угол между векторами. Скалярное произведение векторов Показательные уравнения и неравенства
Показательные уравнения и неравенства Презентация по математике "Многочлен и его стандартный вид" - скачать
Презентация по математике "Многочлен и его стандартный вид" - скачать  Презентация на тему Графический метод решения системы линейных уравнений
Презентация на тему Графический метод решения системы линейных уравнений  Биквадратное уравнение
Биквадратное уравнение Умножение десятичных дробей
Умножение десятичных дробей