Содержание
- 2. IV. 0. Элементы ТВ и МС Cтатистический (стохастический) эксперимент - эксперимент, результат которого заранее неизвестен. Лежит
- 3. IV. 0. Элементы ТВ и МС Случайная величина и ее вероятность связаны функциями: 1. Зависимость между
- 4. IV. 0. Элементы ТВ и МС Числовые характеристики случайной величины: 1. Меры положения - математическое ожидание
- 5. IV. 0. Элементы ТВ и МС 2. Меры разброса - дисперсия D– математическое ожидание квадрата отклонения
- 6. IV. 0. Элементы ТВ и МС 3. Меры формы. Функция плотности распределения f(x) может быть: -
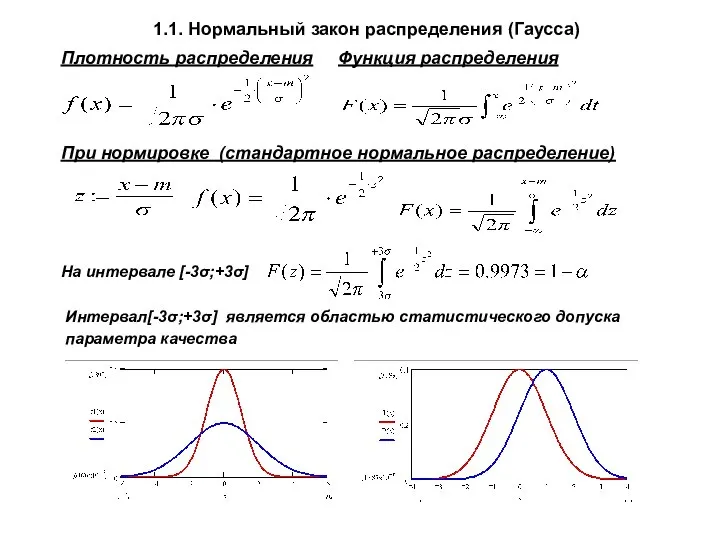
- 7. 1.1. Нормальный закон распределения (Гаусса) Плотность распределения Функция распределения При нормировке (стандартное нормальное распределение) На интервале
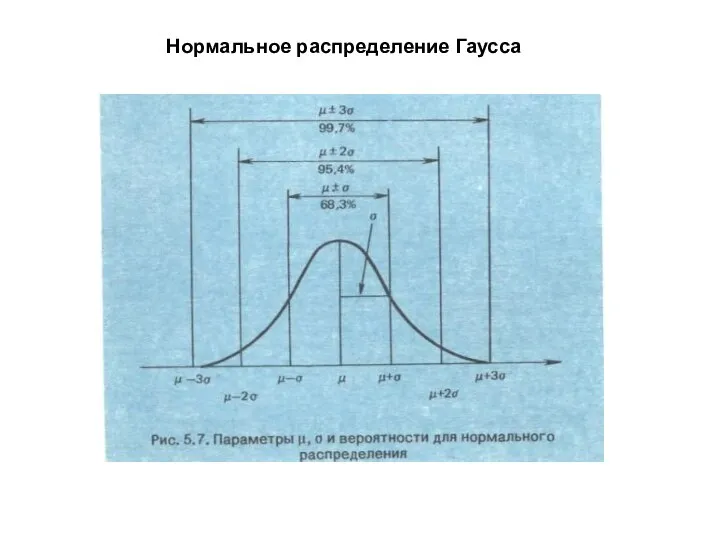
- 8. Нормальное распределение Гаусса
- 9. IV. 0. Элементы математической статистики Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации,
- 10. IV.0. Элементы математической статистики Все изучаемые объекты формируют генеральную совокупность ( ГС) данных. Объем генеральной ГС
- 11. Варианта - наблюдаемое значение количественного признака хi, Вариационный ряд - последовательность вариант, записанных в порядке возрастания
- 12. Элементы математической статистики и производственный процесс. Долгосрочная и краткосрочная вариации Производственный процесс может отслеживаться в текущем
- 13. Существует аналогия между статистическим распределением выборки и законом распределения дискретной случайной величины. В данном случае вместо
- 14. Графическое представление экспериментальных данных Экспериментальные данные по мере наблюдений заносятся в таблицы определенной формы. Для наглядного
- 15. Корреляционный, регрессионный, дисперсионный, временной анализ Основная задача корреляционного анализа – выявление связи между случайными переменными Основная
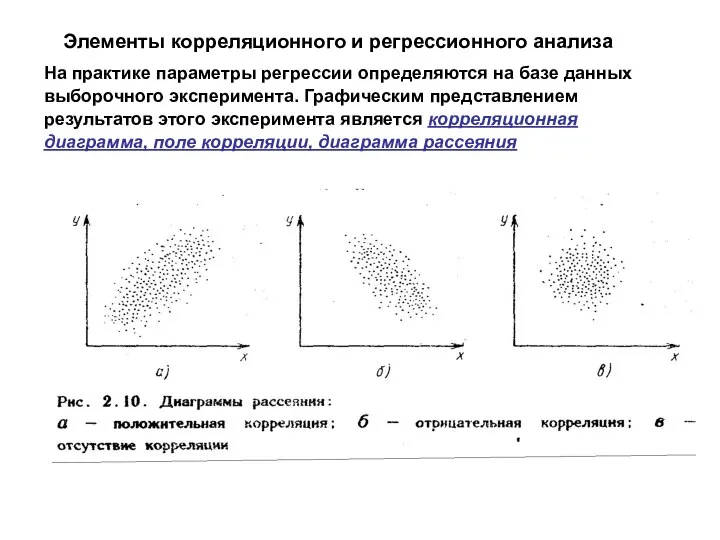
- 16. Элементы корреляционного и регрессионного анализа На практике параметры регрессии определяются на базе данных выборочного эксперимента. Графическим
- 17. Корреляция. Поле корреляции По виду диаграммы рассеяния можно судить о характере и силе корреляционной связи. Если
- 18. Статистическая связь между одним фактором и средним значением другого может быть сильной, слабой, отсутствовать. Уравнение регрессии
- 20. Скачать презентацию














 Методические рекомендации по подготовке к ГИА-9 по математике (для учителей, родителей, учащихся) Особенности методическ
Методические рекомендации по подготовке к ГИА-9 по математике (для учителей, родителей, учащихся) Особенности методическ Разложение функций в степенные ряды. Приближенное вычисление значений функции. Интегрирование функций. (Семинар 28)
Разложение функций в степенные ряды. Приближенное вычисление значений функции. Интегрирование функций. (Семинар 28) 7 увлекательных задач от советского математика
7 увлекательных задач от советского математика Подготовка к ЕГЭ (решение заданий С2,С4)
Подготовка к ЕГЭ (решение заданий С2,С4) Отношения. Определение
Отношения. Определение Подобие треугольников
Подобие треугольников Как математика помогла мне сделать открытия. Проект
Как математика помогла мне сделать открытия. Проект Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11
Урок математики в 6 «в» классе «Алгоритм решения задач на пропорции» Учитель: Лиманская Ю. И МОУ СОШ №11 Круговые диаграммы
Круговые диаграммы Аттестационная работа. Решение задач по формуле Пика
Аттестационная работа. Решение задач по формуле Пика Десятичная запись дробных чисел
Десятичная запись дробных чисел Шестое математическое действие
Шестое математическое действие Презентация на тему Мир правильных многогранников
Презентация на тему Мир правильных многогранников  ЕГЭ Математика
ЕГЭ Математика Признаки параллельности двух прямых
Признаки параллельности двух прямых Квадратичная функция
Квадратичная функция Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Логические операции И ИЛИ
Логические операции И ИЛИ Урок математики в 1 классе. Перестановка слагаемых
Урок математики в 1 классе. Перестановка слагаемых Методика изучения длины в процесе изучения геометрического материала
Методика изучения длины в процесе изучения геометрического материала Деление одночлена на одночлен. 7 класс. Урок 49
Деление одночлена на одночлен. 7 класс. Урок 49 Отношение эквивалентности и фактор-множество
Отношение эквивалентности и фактор-множество Замена переменной и формула интегрирования по частям в определенном интеграле
Замена переменной и формула интегрирования по частям в определенном интеграле Учитель математики МОУ СОШ №73 им.А.Ф. Чернонога
Учитель математики МОУ СОШ №73 им.А.Ф. Чернонога  Возрастание и убывание функций
Возрастание и убывание функций Жиындар
Жиындар Эти увлекательные и занимательные задачи. 5 класс
Эти увлекательные и занимательные задачи. 5 класс Занятие по формированию элементарных математических представлений. Тема Насекомые
Занятие по формированию элементарных математических представлений. Тема Насекомые