Содержание
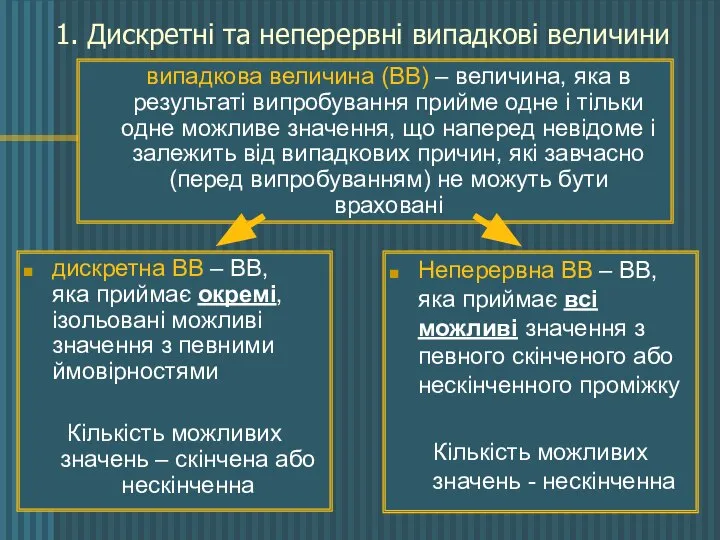
- 2. 1. Дискретні та неперервні випадкові величини дискретна ВВ – ВВ, яка приймає окремі, ізольовані можливі значення
- 3. 2. Закон розподілу ймовірностей ДВВ Закон розподілу ДВВ – відповідність між можливими значеннями ВВ і їх
- 4. Приклад: Умова: У клітці 20 щурів: 1 – білий, 10 – сірих і 9 чорних. Навмання
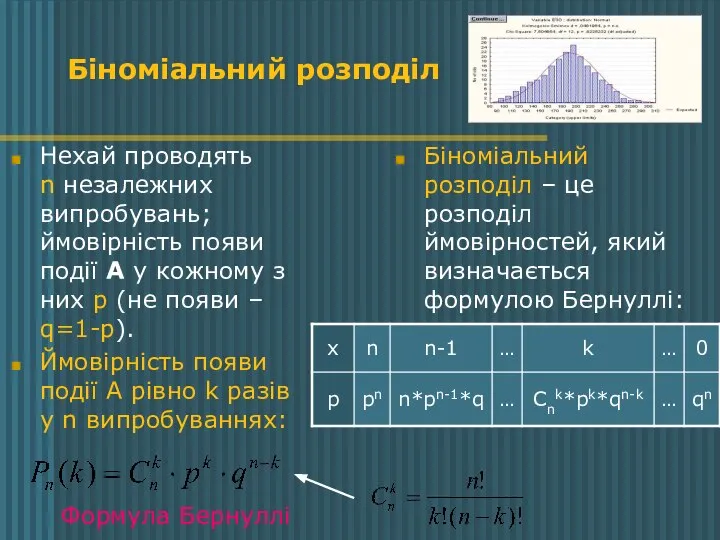
- 5. Біноміальний розподіл Нехай проводять n незалежних випробувань; ймовірність появи події А у кожному з них р
- 6. Найімовірніше число появи події А у випадку біноміального розподілу:
- 7. Приклад: Умова: У сім’ї народилась трійня. Знайти закон розподілу кількості хлопчиків, коли ймовірність народження хлопчика =
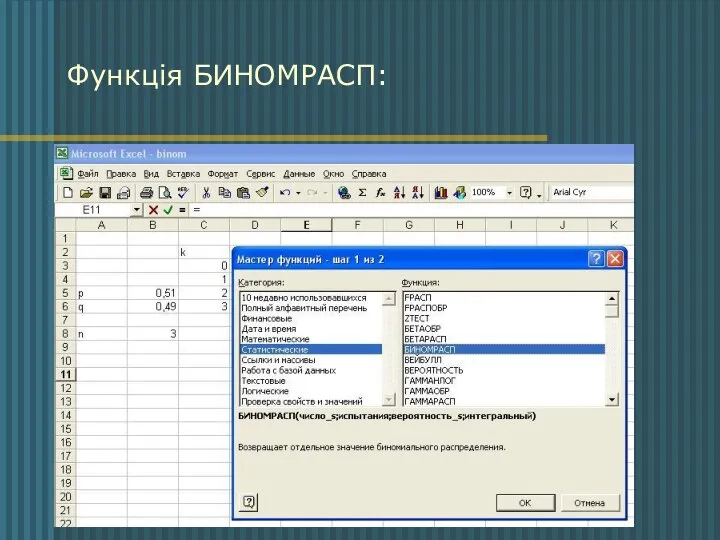
- 8. Функція БИНОМРАСП:
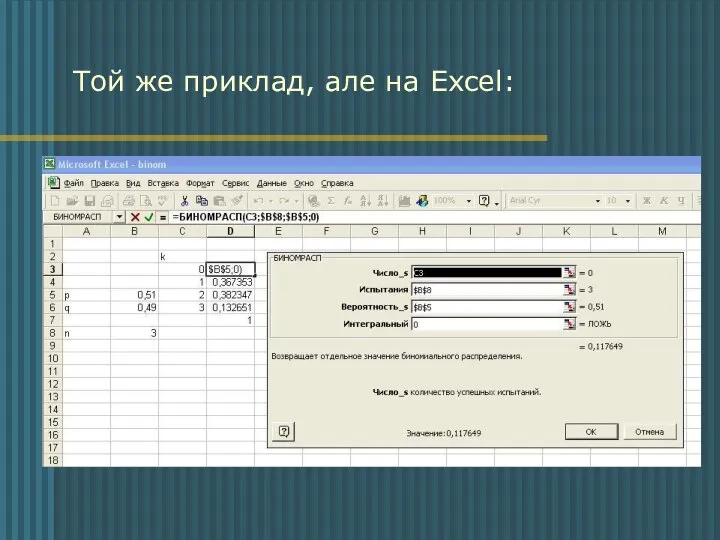
- 9. Той же приклад, але на Excel:
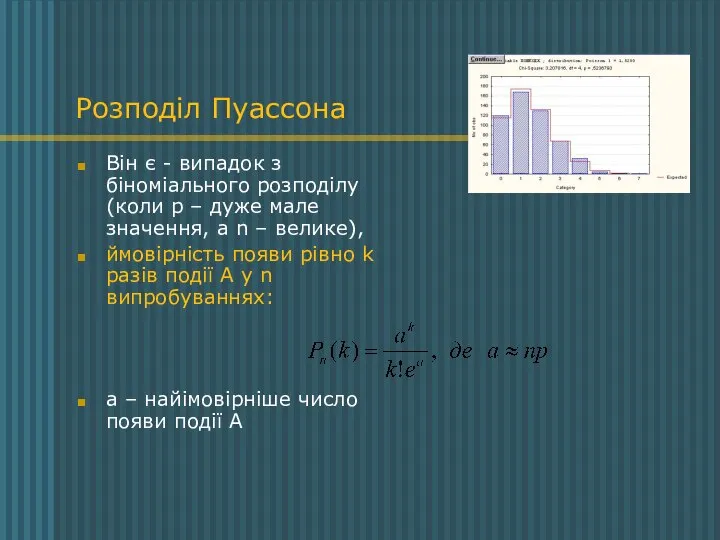
- 10. Розподіл Пуассона Він є - випадок з біноміального розподілу (коли р – дуже мале значення, а
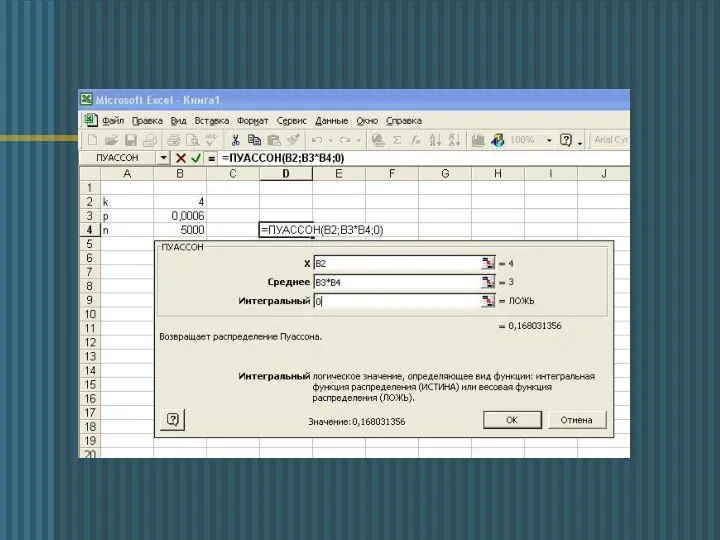
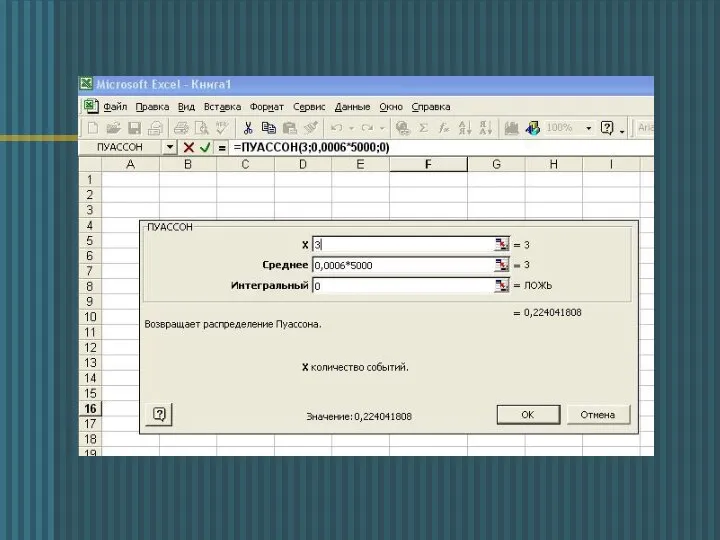
- 11. Приклад: Умова: Підручник зі статистики видано тиражем 5 000 примірників. Ймовірність неправильного брошурування = 0,0006. а)
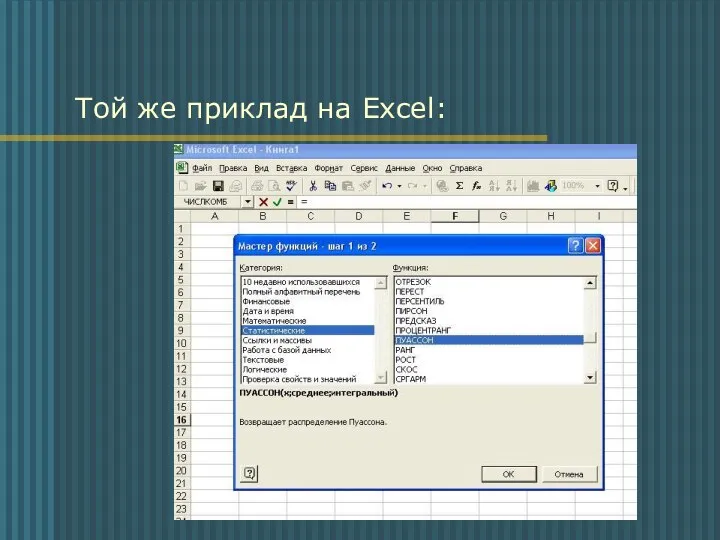
- 12. Той же приклад на Excel:
- 15. 3. Числові характеристики ДВВ і їх властивості Математичне сподівання – це характеристика середнього значення ВВ; -
- 16. Дисперсія: - характеристика розсіяння можливих значень ВВ навколо М(Х) - це математичне сподівання квадрату відхилень ВВ
- 17. Середнє квадратичне відхилення: - характеристика розсіяння можливих значень ВВ навколо М(Х) - це квадратний корінь з
- 18. Приклад: Знайти математичне сподівання, дисперсію і середнє квадратичне відхилення для даних ймовірності появи хлопчиків у трійні:
- 19. 3. Неперервні ВВ. Нормальний розподіл. Випадкова величина Х є нормально розподіленою, коли її функція густини (значення
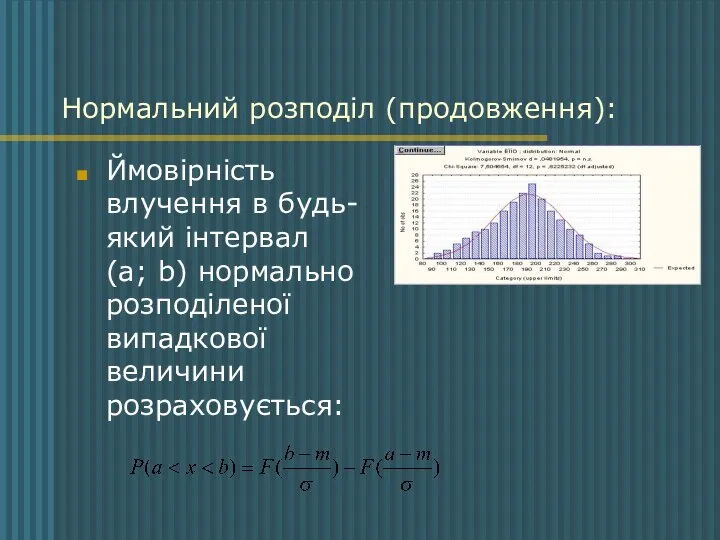
- 20. Нормальний розподіл (продовження): Ймовірність влучення в будь-який інтервал (a; b) нормально розподіленої випадкової величини розраховується:
- 21. Нормальний розподіл (продовження): Ймовірність того, що абсолютна величина відхилення менше додатного числа у Правило 2 та
- 22. Приклад: Математичне сподівання нормально розподіленої випадкової величини Х дорівнює 3, середньоквадратичне відхилення = 2. Написати густину
- 23. Приклад: Математичне сподівання і середньоквадратичне відхилення нормально розподіленої випадкової величини Х, відповідно, дорівнюють 10 і 2.
- 25. Скачать презентацию













 Логарифмические уравнения
Логарифмические уравнения Практические приложения подобия треугольников. (Примеры из книги Я.И. Перельман «Занимательная геометрия»).
Практические приложения подобия треугольников. (Примеры из книги Я.И. Перельман «Занимательная геометрия»).  Взаимосвязь математики и архитектуры в симметрии
Взаимосвязь математики и архитектуры в симметрии Векторы. Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов. Прямая на плоскости
Векторы. Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов. Прямая на плоскости Автор: С.А.Данилова учитель математики ГБОУСОШ№625 с углубленным изучением математики Невского района Санкт-Петербурга им. Ге
Автор: С.А.Данилова учитель математики ГБОУСОШ№625 с углубленным изучением математики Невского района Санкт-Петербурга им. Ге Решение уравнений. Устная разминка
Решение уравнений. Устная разминка Десятки и единицы
Десятки и единицы Презентация по математике Дробные числа Урок математики в 6 классе
Презентация по математике Дробные числа Урок математики в 6 классе  Как измеряли в древности. (5 класс)
Как измеряли в древности. (5 класс) Інтерполяційний многочлен Ньютона. (Лекція 3)
Інтерполяційний многочлен Ньютона. (Лекція 3) Преобразование графиков функций
Преобразование графиков функций Основное свойство дроби
Основное свойство дроби Значение логико-математических игр в умственном и речевом развитии детей старшего дошкольного возраста
Значение логико-математических игр в умственном и речевом развитии детей старшего дошкольного возраста Взаимно обратные числа
Взаимно обратные числа Прямоугольник. Измерение площадей фигур
Прямоугольник. Измерение площадей фигур Подготовка к ГИА по математике. Задания 7
Подготовка к ГИА по математике. Задания 7 Многочлен и его стандартный вид
Многочлен и его стандартный вид Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Презентация на тему Устный счет
Презентация на тему Устный счет Статистические методы обработки информации
Статистические методы обработки информации Понятие модели. Способы представления моделей. (Лекция 4)
Понятие модели. Способы представления моделей. (Лекция 4) Теория графов в задачах
Теория графов в задачах Многомерные случайные величины
Многомерные случайные величины Решение задач по статистическому моделированию. Моделирование систем
Решение задач по статистическому моделированию. Моделирование систем Вероятность совместных и несовместных событий
Вероятность совместных и несовместных событий Ипотека : математика в экономике (математика вокруг нас). 10кл (1)
Ипотека : математика в экономике (математика вокруг нас). 10кл (1) Алгебра и начало анализа. Функция y=cos x
Алгебра и начало анализа. Функция y=cos x Теорема Безу. Схема Горнера и её применения
Теорема Безу. Схема Горнера и её применения