Содержание
- 2. Рассмотрим 3-х мерное пространство. Если точкам области поставить в соответствие точки в пространстве то все точки
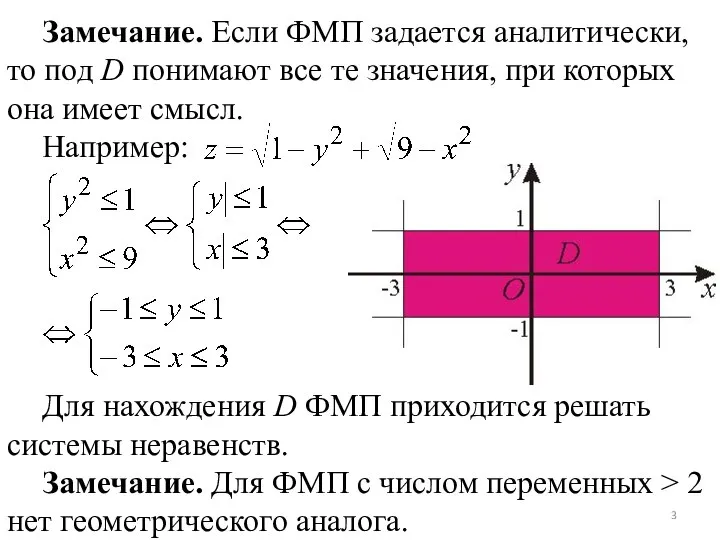
- 3. Замечание. Если ФМП задается аналитически, то под D понимают все те значения, при которых она имеет
- 4. § 2. Предел функции многих переменных. Непрерывность функции многих переменных. Определение3.Число А называется пределом фун- кции
- 5. если предел зависит от способа приближения к точке (x0,y0), то в этом случае говорят, что предел
- 6. т.е. Определение 6. Функция z = f (x,y) называется непрерывной в точке (x0,y0), если ∀ ε
- 7. Определение 7. Функция z = f (x,y) называется непрерывной в точке (x0,y0), если . Замечание. Все
- 8. § 3. Производные функций многих переменных. Их геометрический смысл. Пусть функция z = f (x,y) определена
- 9. Определение 8. Если существует конечный предел отношения при Δx → 0, то этот предел называется частной
- 10. Определение 9. Если существует конечный предел отношения Δyz = f (x0, y0 + Δy) – f
- 11. Геометрический смысл частной производной - это тангенс угла наклона касательной, проведенной к графику функции z1 =
- 12. § 4. Дифференцируемость. Дифференциал функции двух переменных. Определение 10. Функция z = f (x,y) называется дифференцируемой
- 13. Определение 11. Дифференциалом функции z = f (x,y) в точке M(x0,y0) называется главная линейная часть приращения
- 14. Теорема 2. Если функция z = f (x,y) дифференцируема в окрестности точки M(x0,y0), то в точке
- 15. Замечание. Встречается обозначение: где: M = M(x0,y0). Если для функции одной переменной существование производной являлось достаточным
- 16. Теорема 3. (Достаточное условие дифференцируемости) Для того, чтобы функция z = f (x,y) была дифференцируема в
- 17. § 5. Касательная плоскость и нормаль к поверхности. Геометрический смысл дифференциала функций двух переменных. Вспомним, что
- 18. Определение 12. Плоскость называется касательной к поверхности z = f (x,y) в точке M(x0,y0), если поверхность
- 19. Теорема 4. (Существование плоскости, касательной к поверхности) Если z = f (x,y) дифференцируема в точке M(x0,y0),
- 20. то направляющий вектор нормали к поверхности имеет вид: Следствие 2. Так как дифференциал функции z =
- 21. Ось z – это ось аппликат. Обозначим: Δx = dx, Δy = dy, тогда: § 6.
- 22. § 12. Экстремумы функции многих переменных. Определение 1. Точка M(x0,y0) называется max (min) функции z =
- 23. Теорема 1. (Необходимое условие существования точки экстремума) Если точка M(x0,y0), является точкой максимума или минимума функции
- 24. Теорема 2. (Достаточное условие существования экстремума) Если в точке M(x0,y0) – критической точке для функции z
- 25. 3) Если выражение Δ(x0,y0) = 0, то требуется дополнительное исследование. Без доказательства. Понятие об условном экстремуме.
- 26. При решении задач на условный экстремум применяется метод множителей Лагранжа. Суть его в следующем: Лагранж предложил
- 27. 2) Применяем достаточное условие экстремума и определяем характер критической точки. Понятие о наибольшем и наименьшем значениях
- 29. Скачать презентацию

























 Множество. Подмножество.
Множество. Подмножество. Применение теоремы Пифагора при решении задач, связанных с работами в сельском хозяйстве
Применение теоремы Пифагора при решении задач, связанных с работами в сельском хозяйстве Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы
Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы  Площадь фигур
Площадь фигур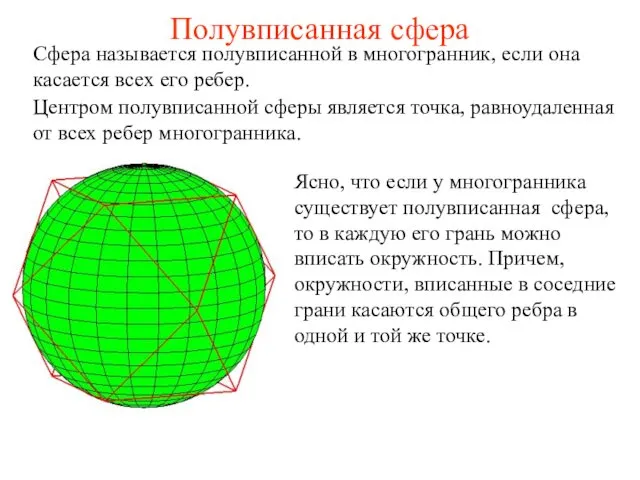 Полувписанная сфера
Полувписанная сфера Решение уравнений. (6 класс)
Решение уравнений. (6 класс) Деление с остатком
Деление с остатком Аттестационная работа. Решение нестандартных задач по математике
Аттестационная работа. Решение нестандартных задач по математике Окружность
Окружность Свойство биссектрисы угла
Свойство биссектрисы угла Деление дробей. Французский математик и физик Паскаль
Деление дробей. Французский математик и физик Паскаль Презентация на тему Система подготовки учащихся к ЕГЭ по математике
Презентация на тему Система подготовки учащихся к ЕГЭ по математике Нахождение дроби от числа
Нахождение дроби от числа Кригинг
Кригинг Презентация по математике "ЧИСЛО И ЦИФРА 5" - скачать бесплатно
Презентация по математике "ЧИСЛО И ЦИФРА 5" - скачать бесплатно Четырёхугольники. Урок - лекция 8 класс
Четырёхугольники. Урок - лекция 8 класс ЭЛЕКТИВНЫЙ КУРС «Алгебра функций» Выполнила: Винник Н.А.- учитель математики 435 школы
ЭЛЕКТИВНЫЙ КУРС «Алгебра функций» Выполнила: Винник Н.А.- учитель математики 435 школы  Ох, уж эти сравнения
Ох, уж эти сравнения Аналитическая геометрия
Аналитическая геометрия Конусның күләме
Конусның күләме Сумма углов треугольника, четырёхугольника
Сумма углов треугольника, четырёхугольника Вычитание чисел 6, 7, 8, 9
Вычитание чисел 6, 7, 8, 9 Решение задач типа в9
Решение задач типа в9 Треугольник. Виды треугольников
Треугольник. Виды треугольников Нахождение целого по его части на основе формального правила
Нахождение целого по его части на основе формального правила МАТЕМАТИКА 5 класс «Б» Тема. Уравнения. Учитель: Славец Е.Н.
МАТЕМАТИКА 5 класс «Б» Тема. Уравнения. Учитель: Славец Е.Н.  Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков
Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков Аттестацианная работа. Исследовательская работа. Фигурные числа
Аттестацианная работа. Исследовательская работа. Фигурные числа