Содержание
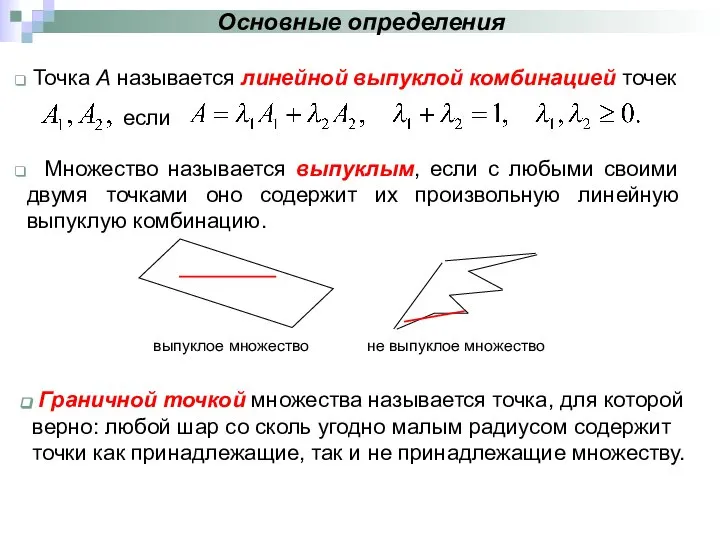
- 2. Основные определения Точка А называется линейной выпуклой комбинацией точек если Множество называется выпуклым, если с любыми
- 5. Множество называется замкнутым, если оно содержит все свои граничные точки. Множество называется ограниченным, если существует шар,
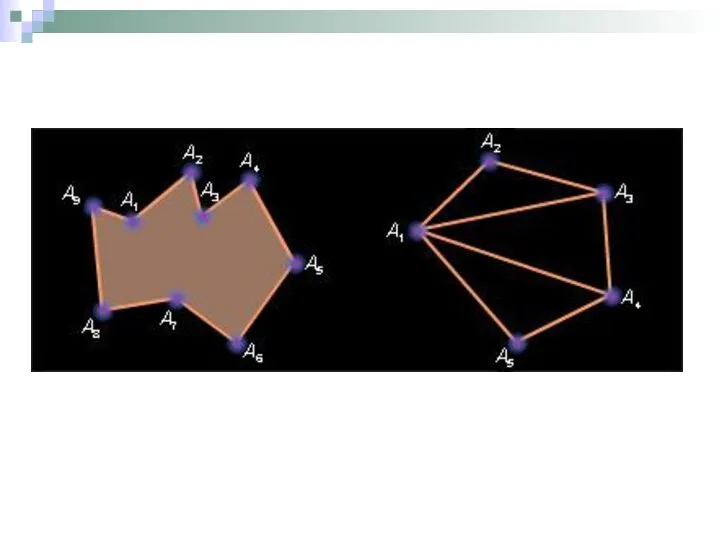
- 6. Теорема Выпуклый замкнутый ограниченный многогранник является выпуклой линейной комбинацией своих угловых точек. Лемма Пересечение любого количества
- 7. Доказательство Докажем, что любая точка треугольника удовлетворяет теореме. В треугольнике A1А2А3 (рис.2.3) возьмем произвольную точку А4
- 8. Геометрическая интерпретация задач линейного программирования
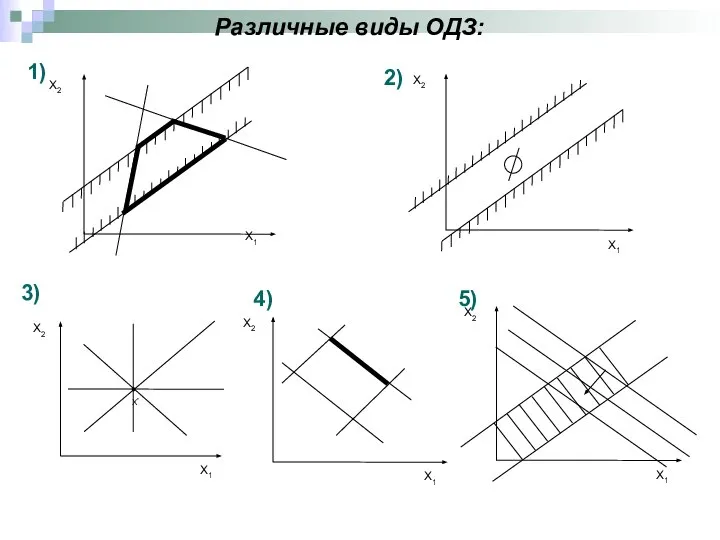
- 10. Различные виды ОДЗ: 1) 3) 2) 4) 5)
- 11. - семейство прямых – линии уровня целевой функции. Линии уровня в пространстве параллельны. (градиент) f =
- 12. Свойства решений ЗЛП Теорема 1 Т е о р е м а 1. Множество всех планов
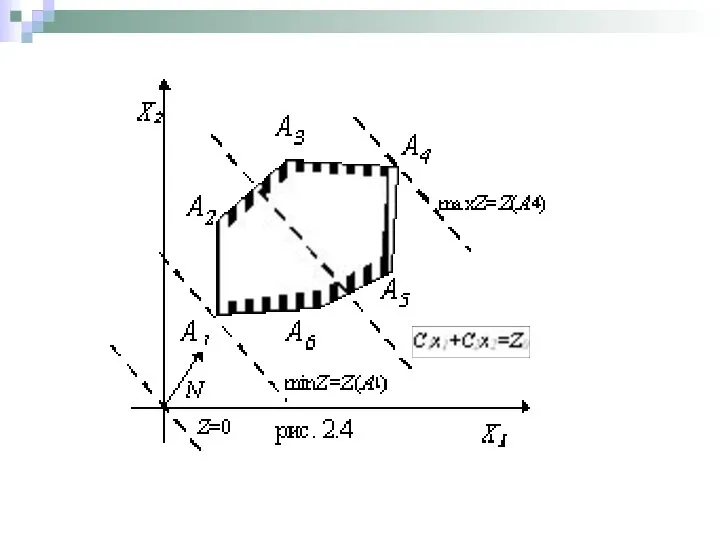
- 13. Теорема 2 Целевая функция ЗЛП достигает своего минимального (максимального) значения в угловой точке многогранника решений. Если
- 14. Доказательство. Предположим, что многогранник решений ограниченный, имеющий конечное число угловых точек. Обозначим его через К. В
- 15. В этом разложении среди значений Z(Xi) (i = 1, 2, ..., p) выберем наименьшее [пусть оно
- 16. Графический метод решения задачи линейного программирования Пусть задача линейного программирования задана в двумерном пространстве, т. е.
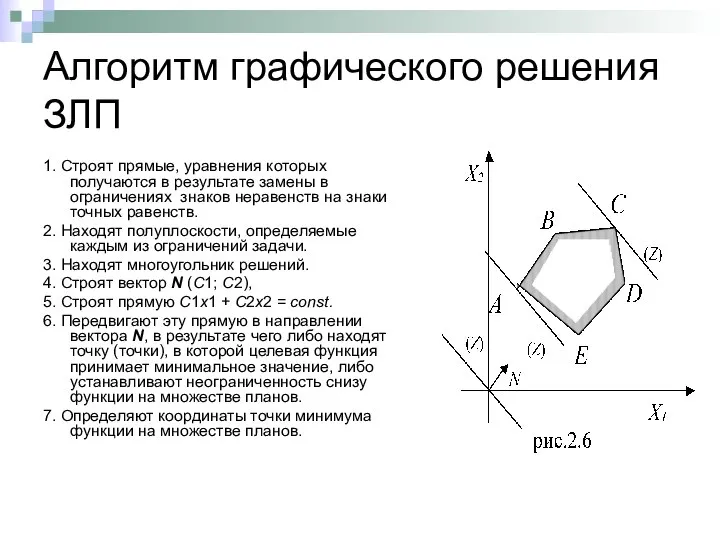
- 17. Алгоритм графического решения ЗЛП 1. Строят прямые, уравнения которых получаются в результате замены в ограничениях знаков
- 19. Симплекс-метод
- 20. Идея симплекс-метода Решение основной задачи линейного программирования геометрическим методом является наглядным в случае двух и даже
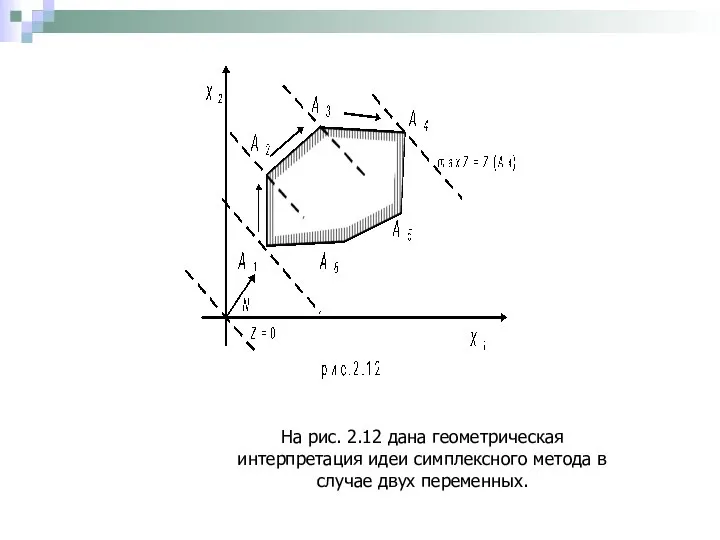
- 21. На рис. 2.12 дана геометрическая интерпретация идеи симплексного метода в случае двух переменных.
- 25. Теорема 2 Если исходная задача решается на максимум, то в – неотрицательные, оптимальное решение исходной задачи.
- 26. Теорема 3 Если опорный план ЗЛП не вырожден и такое, что в k-ом столбце системы ограничений
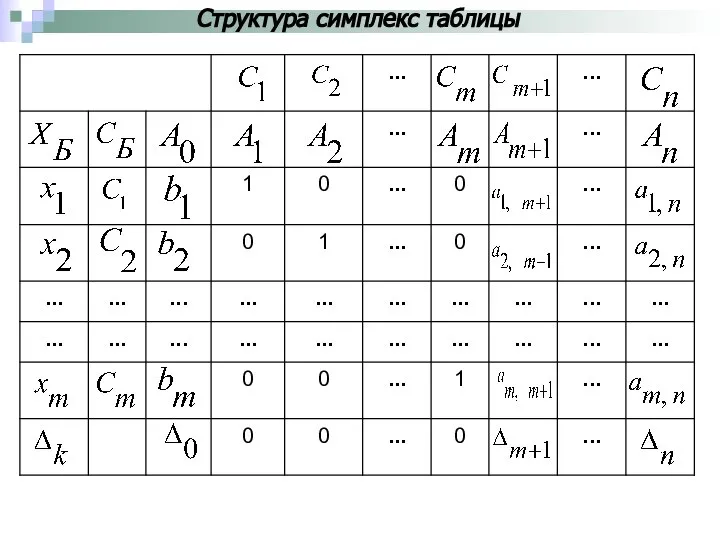
- 27. Структура симплекс таблицы
- 29. Скачать презентацию



















 Сравнение чисел
Сравнение чисел Введение в теорию игр
Введение в теорию игр Фрактальная графика
Фрактальная графика Визначений інтеграл
Визначений інтеграл Луч и угол. (7 класс)
Луч и угол. (7 класс) Задачи на смеси, сплавы, растворы
Задачи на смеси, сплавы, растворы Квадратный корень. Математический диктант
Квадратный корень. Математический диктант Математические ребусы
Математические ребусы Решение уравнений, приводимых к квадратным
Решение уравнений, приводимых к квадратным Десятичная дробь. Графический диктант
Десятичная дробь. Графический диктант Требования к оформлению печатных проектно-исследовательских работ
Требования к оформлению печатных проектно-исследовательских работ Зеркальная симметрия и параллельный перенос
Зеркальная симметрия и параллельный перенос Вынесение общего множителя за скобки
Вынесение общего множителя за скобки Вычисление площади треугольника
Вычисление площади треугольника Время. Решение задач
Время. Решение задач Проверка гипотез. Основы ДА
Проверка гипотез. Основы ДА Correlation and regression
Correlation and regression Координатная плоскость. (6 класс)
Координатная плоскость. (6 класс) Математический тренажёр «Бабушкины примеры»
Математический тренажёр «Бабушкины примеры» Треугольники. Практика. Первый уровень
Треугольники. Практика. Первый уровень Путешествия на тропинках математики
Путешествия на тропинках математики Координаты вектора
Координаты вектора Кружок Занимательная математика
Кружок Занимательная математика Таблицы сложения и вычитания с числом 2
Таблицы сложения и вычитания с числом 2 Случайные процессы
Случайные процессы Степень числа. Квадрат и куб числа. Математика, 5 класс
Степень числа. Квадрат и куб числа. Математика, 5 класс Прямая в пространстве
Прямая в пространстве Проценты. 5 класс. Урок № 3
Проценты. 5 класс. Урок № 3