Содержание
- 3. Пример. Решение.
- 4. 2) В параметрической форме.
- 5. Вычислить площадь эллипса. Пример. Решение. Уравнения эллипса в параметрической форме:
- 6. 3) В полярных координатах.
- 7. Пример. Решение.
- 8. 1) В декартовых координатах. 2) В параметрической форме.
- 9. Пример. Вычислить длину витка винтовой линии Решение.
- 10. 3) В полярных координатах. Пример. Решение.
- 11. 1) В декартовых координатах. 2) В параметрической форме.
- 12. 3) В полярных координатах.
- 13. - площадь любого сечения тела плоскостью, перпендикулярной оси Оx. Вычисление объёмов по заданным площадям поперечных сечений.
- 14. Пример. Решение. Основание треугольника
- 16. 2) Вычисление объёмов тел вращения.
- 17. Пример. Решение.
- 18. Несобственные интегралы. называется несобственным интегралом первого рода.
- 19. Если предел существует и конечен, то несобственный интеграл называется сходящимся. Если предел не существует, или бесконечен,
- 20. Обобщённая формула Ньютона-Лейбница. Точно также,
- 21. Вычислить несобственные интегралы, или доказать что они расходятся. (сходится) Пример. (расходится) (предел не существует, поэтому интеграл
- 22. Признаки сходимости интегралов с бесконечными пределами. Признаки сравнения
- 23. то интегралы ведут себя одинаково в отношении сходимости и расходимости. и существует конечный предел
- 24. расходится Пример. Исследовать на сходимость Решение.
- 25. Несобственные интегралы второго рода. называется несобственным интегралом второго рода.
- 26. Если предел существует и конечен, то несобственный интеграл называется сходящимся. Если предел не существует, или бесконечен,
- 27. Если каждый из интегралов в правой части равенства сходится, то несобственный интеграл В противном случае –
- 28. Пример. Решение. По обобщенной формуле Ньютона-Лейбница:
- 30. Скачать презентацию


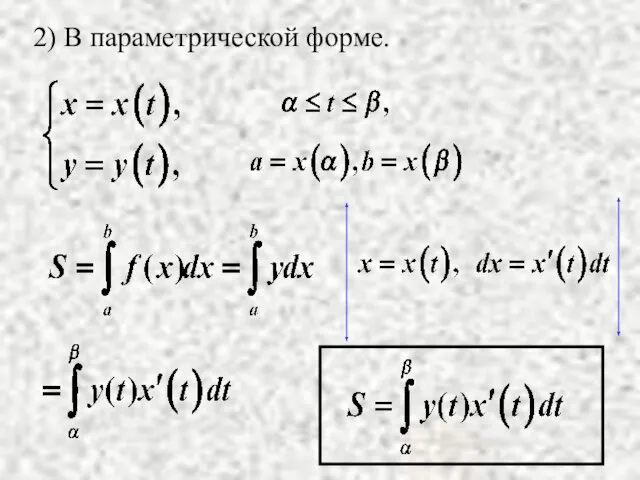





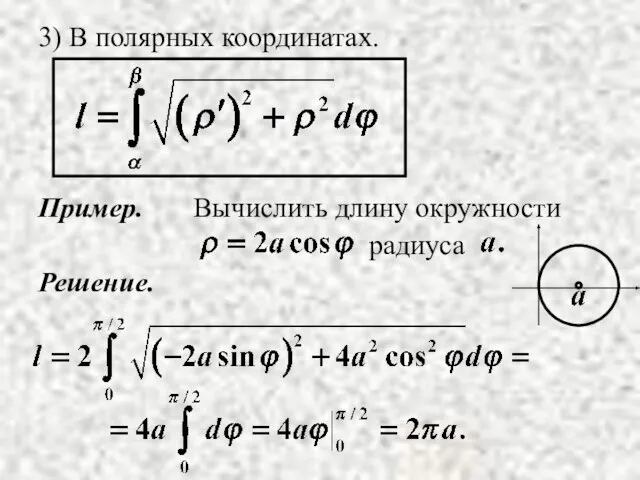

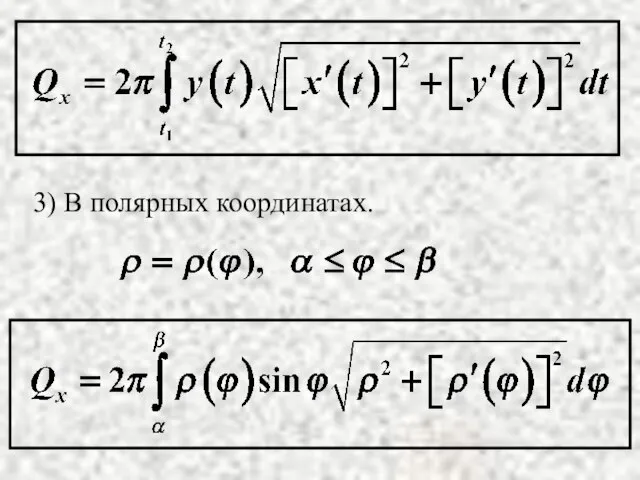
















 Критерий согласия. Практический пример применения критерия согласия. Закон Менделя
Критерий согласия. Практический пример применения критерия согласия. Закон Менделя Область определения и множество значений тригонометрических функций
Область определения и множество значений тригонометрических функций Логарифмическая функция, ее график и свойства
Логарифмическая функция, ее график и свойства Преобразование графиков функций
Преобразование графиков функций УМНИКИ И УМНИЦЫ
УМНИКИ И УМНИЦЫ  Л. В. Барсукова, A. В. Барсткова. Геометрия. Практикум. Учебное пособие
Л. В. Барсукова, A. В. Барсткова. Геометрия. Практикум. Учебное пособие Математические цепочки. Устный счет на уроках математики
Математические цепочки. Устный счет на уроках математики Сравнение десятичных дробей
Сравнение десятичных дробей Презентация по математике "Искусство рассуждать" - скачать бесплатно
Презентация по математике "Искусство рассуждать" - скачать бесплатно Длина окружности и площадь круга
Длина окружности и площадь круга Делители и кратные Артамонова Л.В, учитель математики МКОУ «Москаленский лицей»
Делители и кратные Артамонова Л.В, учитель математики МКОУ «Москаленский лицей»  Обслуговування заявок за пріоритетними дисциплінами
Обслуговування заявок за пріоритетними дисциплінами Свойства цилиндра. Выпуклый и прямой цилиндр
Свойства цилиндра. Выпуклый и прямой цилиндр Презентация Умножение и деление чисел
Презентация Умножение и деление чисел Математика вокруг нас
Математика вокруг нас Презентация Функция в математике
Презентация Функция в математике Классическая вероятность Р. Благоприятные события
Классическая вероятность Р. Благоприятные события Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс
Мой любимый предмет – геометрия. «Геометрия – прообраз красоты мира.» И. Кеплер. 11 класс Решение нестандартных задач Цифры не управляют миром, но они показывают, как управляется мир. (И. Гете) План презентации 1. К
Решение нестандартных задач Цифры не управляют миром, но они показывают, как управляется мир. (И. Гете) План презентации 1. К Презентация по математике "Числа в различных системах счисления" - скачать бесплатно
Презентация по математике "Числа в различных системах счисления" - скачать бесплатно Решение простейших логарифмических уравнений
Решение простейших логарифмических уравнений Круг и отрезок
Круг и отрезок Логика высказываний. Таблицы истинности
Логика высказываний. Таблицы истинности Признаки делимости натуральных чисел
Признаки делимости натуральных чисел Проценты 5 класс
Проценты 5 класс Сравнение чисел. Урок математики в 6 классе
Сравнение чисел. Урок математики в 6 классе Тела Архимеда
Тела Архимеда Презентация на тему Функции у=sin x и y = cos x и их графики
Презентация на тему Функции у=sin x и y = cos x и их графики