Содержание
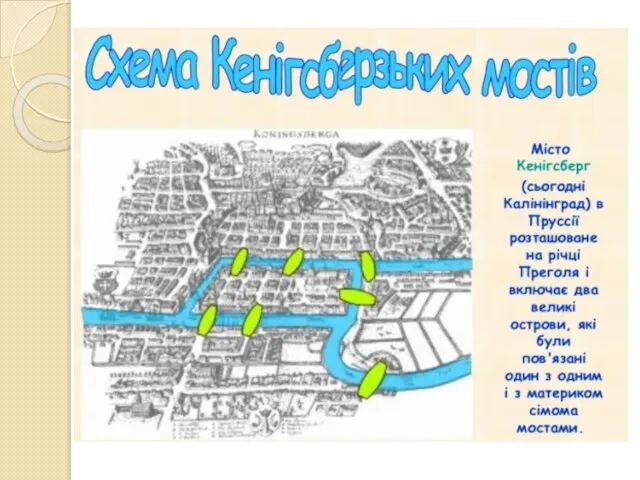
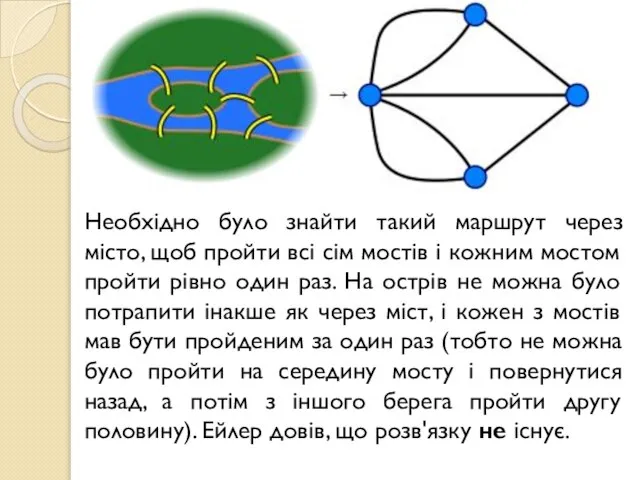
- 3. Необхідно було знайти такий маршрут через місто, щоб пройти всі сім мостів і кожним мостом пройти
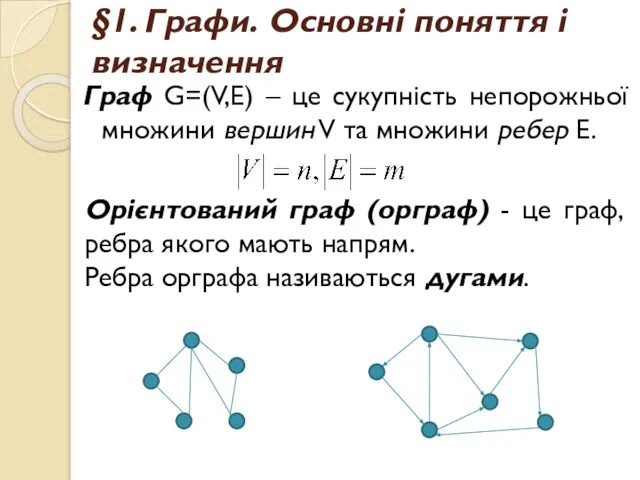
- 4. §1. Графи. Основні поняття і визначення Граф G=(V,E) – це сукупність непорожньої множини вершин V та
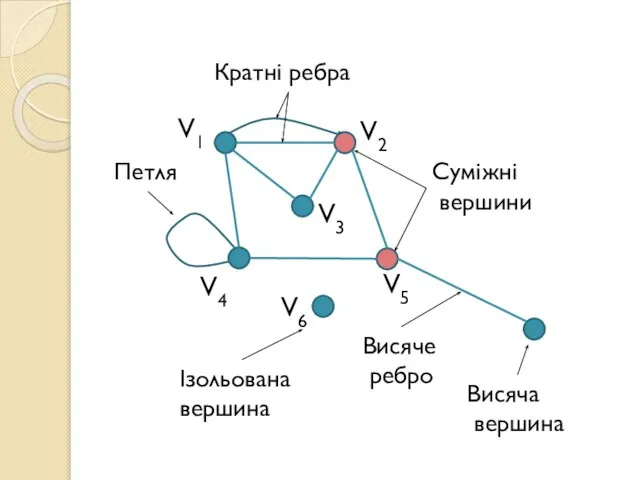
- 5. За наочного подавання графа вершини зображуються точками, ребра – лініями, які з’єднують точки. Кількість ребер, інцидентних
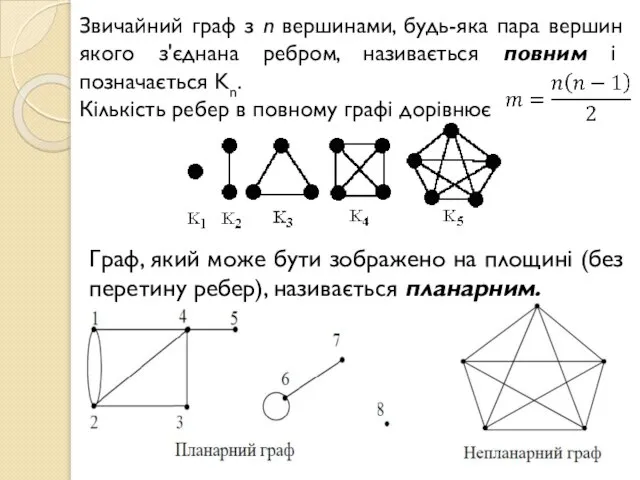
- 7. Звичайний граф з n вершинами, будь-яка пара вершин якого з'єднана ребром, називається повним і позначається Kn.
- 8. Теорема 1. Сума степенів усіх вершин графа дорівнює подвоєній кількості ребер. Д о в е д
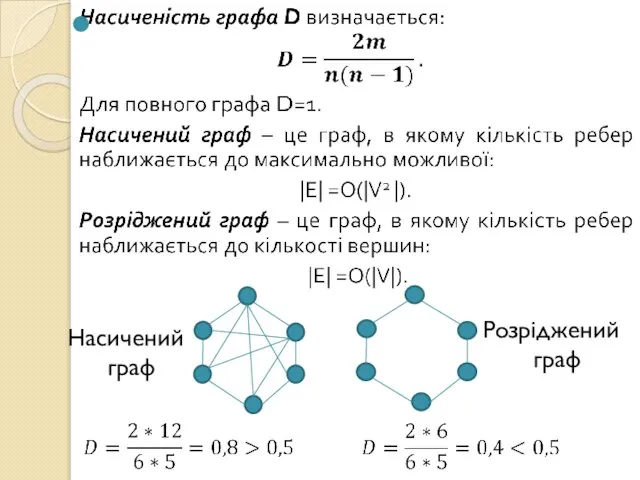
- 9. Насичений граф Розріджений граф
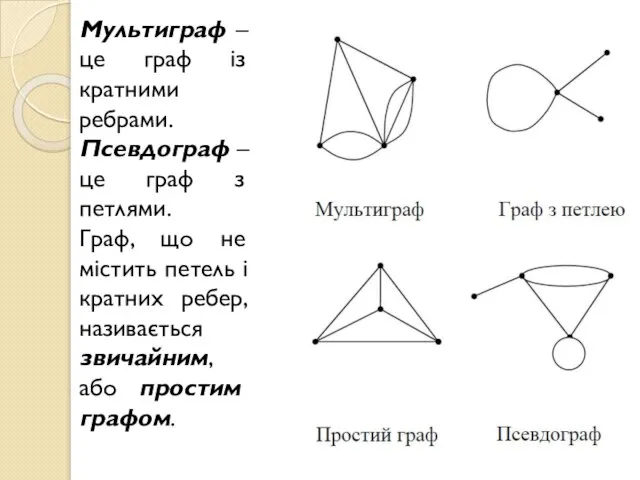
- 10. Мультиграф – це граф із кратними ребрами. Псевдограф – це граф з петлями. Граф, що не
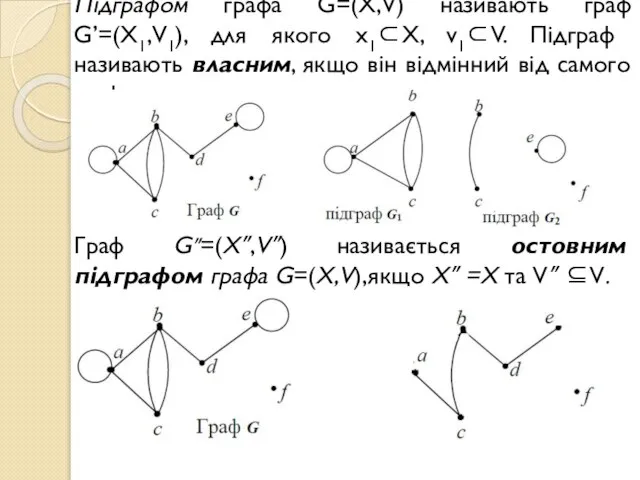
- 11. Підграфом графа G=(X,V) називають граф G’=(X1,V1), для якого х1⊂X, v1⊂V. Підграф називають власним, якщо він відмінний
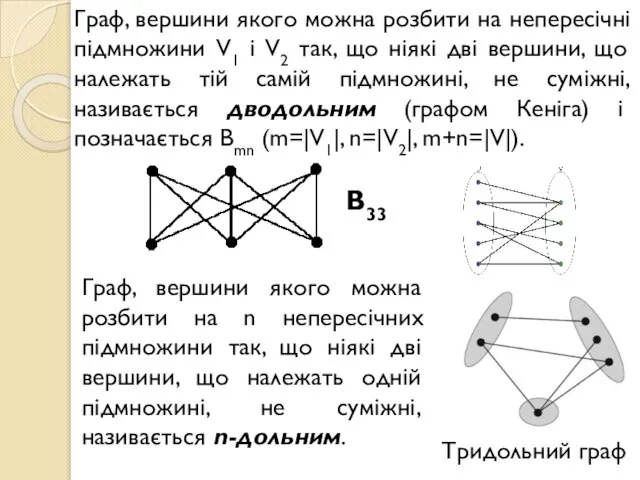
- 12. Граф, вершини якого можна розбити на непересічні підмножини V1 і V2 так, що ніякі дві вершини,
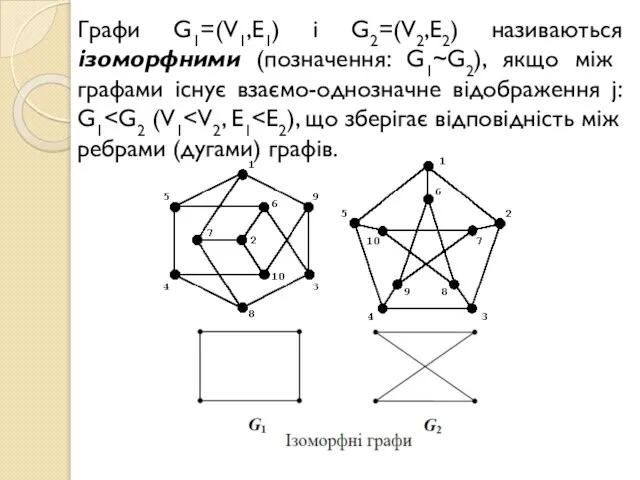
- 13. Графи G1=(V1,E1) і G2=(V2,E2) називаються ізоморфними (позначення: G1~G2), якщо між графами існує взаємо-однозначне відображення j: G1
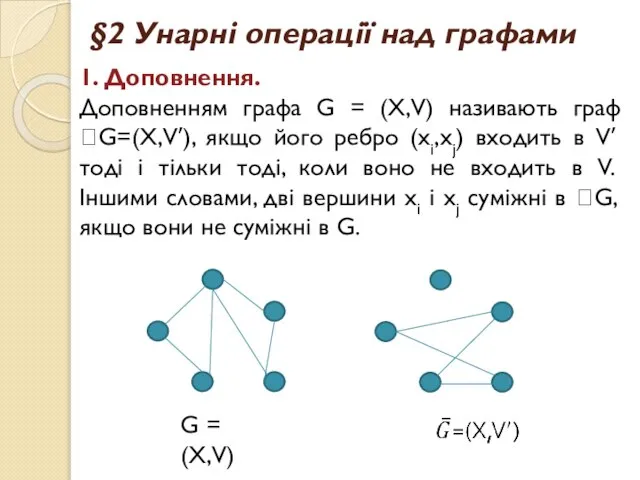
- 14. §2 Унарні операції над графами 1. Доповнення. Доповненням графа G = (X,V) називають граф G=(X,V′), якщо
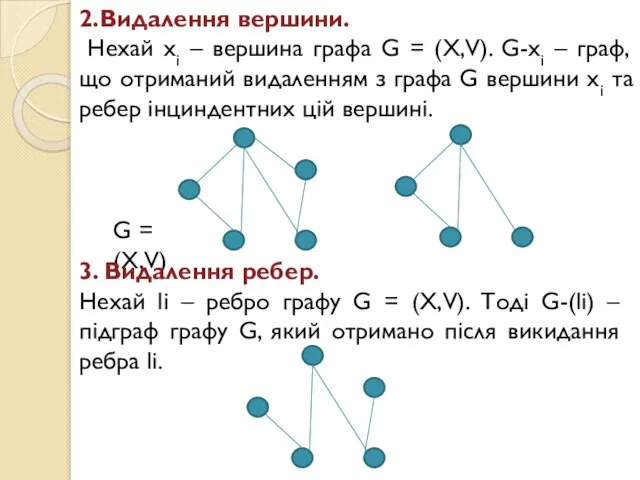
- 15. 2.Видалення вершини. Нехай xi – вершина графа G = (X,V). G-xi – граф, що отриманий видаленням
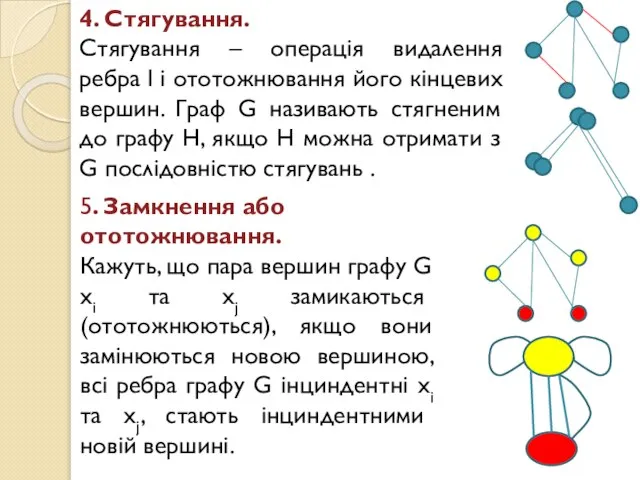
- 16. 4. Стягування. Стягування – операція видалення ребра l і ототожнювання його кінцевих вершин. Граф G називають
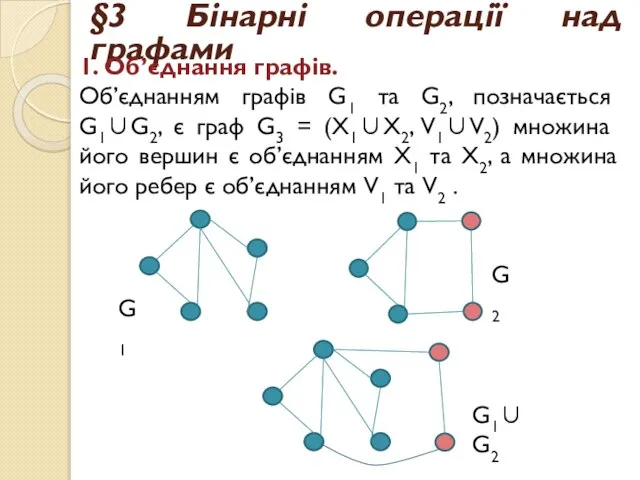
- 17. §3 Бінарні операції над графами 1. Об’єднання графів. Об’єднанням графів G1 та G2, позначається G1∪G2, є
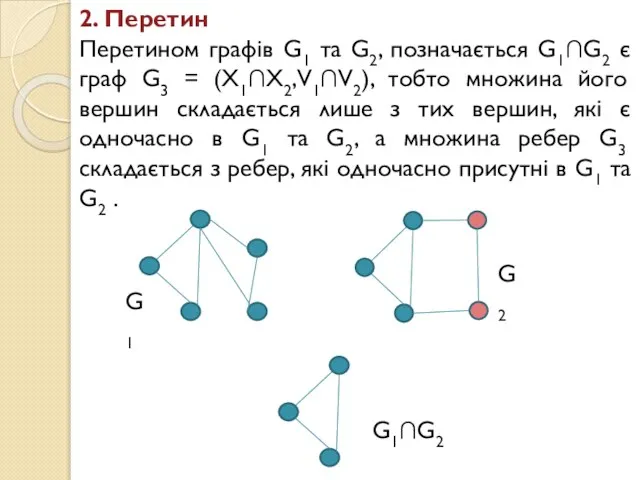
- 18. 2. Перетин Перетином графів G1 та G2, позначається G1∩G2 є граф G3 = (X1∩X2,V1∩V2), тобто множина
- 20. Скачать презентацию


 КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку
КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку  Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Цилиндр. Конус
Цилиндр. Конус Что такое математика?
Что такое математика? Неравенства. Методика систематизации знаний при подготовке к ГИА
Неравенства. Методика систематизации знаний при подготовке к ГИА Первообразные
Первообразные Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости
Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости Цель диагностики математического развития детей
Цель диагностики математического развития детей Свойства действий с рациональными числами. Часть 2
Свойства действий с рациональными числами. Часть 2 Предварительный эксперимент и методы его анализа
Предварительный эксперимент и методы его анализа Презентация на тему Скорость сближения и удаления
Презентация на тему Скорость сближения и удаления  Разбор задач
Разбор задач Действия над комплексными числами в алгебраической форме
Действия над комплексными числами в алгебраической форме Математика 1 класс
Математика 1 класс  Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Презентация по математике "Математика – гимнастика ума" - скачать бесплатно
Презентация по математике "Математика – гимнастика ума" - скачать бесплатно Реляционная алгебра. Операторы
Реляционная алгебра. Операторы Связь математики с биологией
Связь математики с биологией Комбинаторика. 5 класс
Комбинаторика. 5 класс Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке
Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке Параллельные алгоритмы вычислительной алгебры. Разделение переменных
Параллельные алгоритмы вычислительной алгебры. Разделение переменных Математика в педиатрии Выполнила:
Математика в педиатрии Выполнила:  Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё
Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё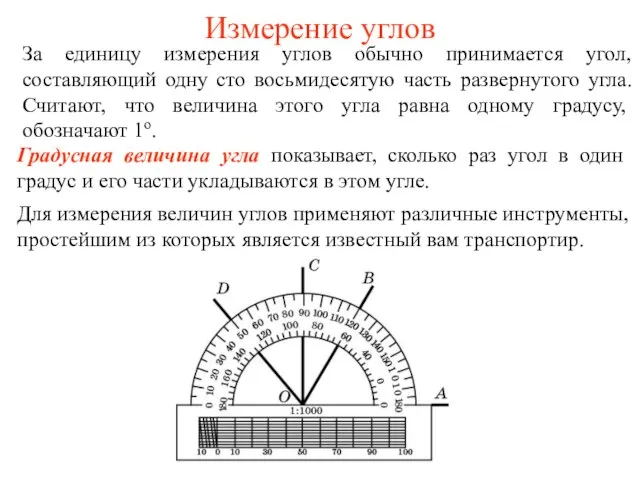 Измерение углов. Вопросы, упражнения
Измерение углов. Вопросы, упражнения Презентация по математике "Логические задачи 1 класс" - скачать бесплатно
Презентация по математике "Логические задачи 1 класс" - скачать бесплатно Тригонометрические уравнения
Тригонометрические уравнения Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения