Содержание
- 2. Этапы графического решения задачи линейного программирования 1. Строят прямые, уравнения которых получаются в результате замены в
- 3. f(X) = 2x1-5x2→max Целевая функция: Ограничения: 3x1 + 2x2 ≥ 6 (1) X1 ≤ 4 (2)
- 4. Построение области допустимых планов 1) Построение границы 1: 3x1 + 2x2 = 6 – прямая линия
- 5. 2 0 3 (1) х1 х2
- 6. 2) Построение границы 2: х1 = 4 –прямая линия Решение неравенства 2: 0 ≤ 4 –
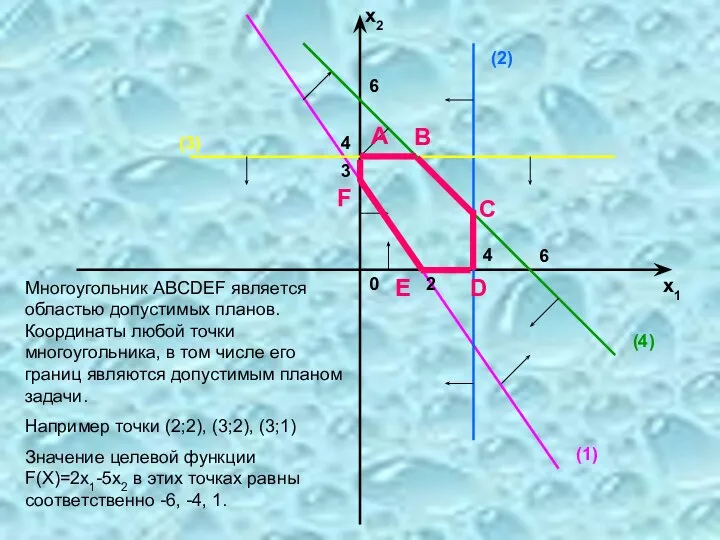
- 7. 0 3 х1 х2 2 4 6 6 4 Многоугольник ABCDEF является областью допустимых планов. Координаты
- 8. II. Оптимизация целевой функции: 1) Построение линии уровня целевой функции: Линия, на которой функция принимает одно
- 9. II. Оптимизация целевой функции: 2) Построение градиента: g = (2; -5) – (коэффициенты при Х в
- 10. 0 3 х1 х2 2 4 6 6 4 -5
- 11. 0 3 х1 х2 2 4 6 6 4 -5
- 12. Передвигаем линию уровня в направлении градиента (если задача на max), при этом значение целевой функции возрастает.
- 13. 0 3 х1 х2 2 4 6 6 4 -5 Х*
- 14. Оптимальный план Х* совпадает с точкой D. Чтобы вычислить значения плана необходимо вычислить координаты точки пересечения
- 15. Оптимальный план Х* = (4; 0) Максимальное значение целевой функции: max f(X) = f(X*) = 2*4
- 16. Непустое множество планов основной задачи линейного программирования образует выпуклый многогранник. Каждая вершина этого многогранника определяет опорный
- 17. Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая
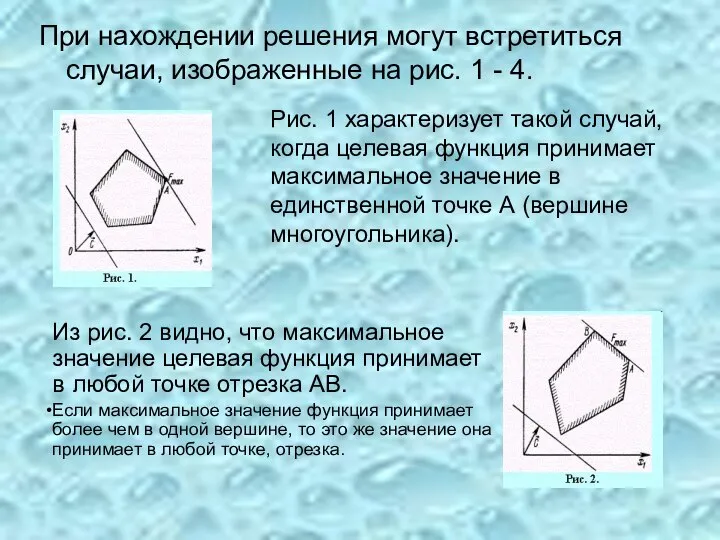
- 18. При нахождении решения могут встретиться случаи, изображенные на рис. 1 - 4. Из рис. 2 видно,
- 19. На рис. 3 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений. На
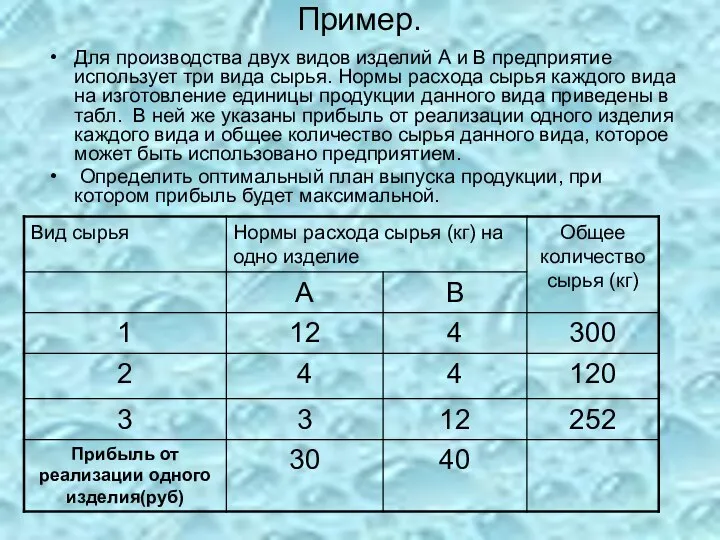
- 20. Пример. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода
- 21. Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой
- 23. Скачать презентацию

















 Презентация по математике "Перпендикулярные прямые" - скачать бесплатно
Презентация по математике "Перпендикулярные прямые" - скачать бесплатно Презентация на тему Повторение сложения и вычитания в пределах 100 и таблицы умножения
Презентация на тему Повторение сложения и вычитания в пределах 100 и таблицы умножения  Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе)
Построение сечений тетраэдра и параллелепипеда (урок геометрии в 10 классе) Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Основные понятия в математической статистике
Основные понятия в математической статистике Множества и операции над ними
Множества и операции над ними Проект подготовили Тикунов Никита 10’Б’ Хубаева Анна 10”Б”. Руководитель Фарух Наталья Евгеньевна.
Проект подготовили Тикунов Никита 10’Б’ Хубаева Анна 10”Б”. Руководитель Фарух Наталья Евгеньевна.  Подготовка к контрольной работе (Параграфы 7-10). Математика
Подготовка к контрольной работе (Параграфы 7-10). Математика Шар в задачах ЕГЭ
Шар в задачах ЕГЭ Современные подходы в обучении математике. ФГОС ОО
Современные подходы в обучении математике. ФГОС ОО Палиндром. Репдиджит. Репьюниты. (6 класс)
Палиндром. Репдиджит. Репьюниты. (6 класс) Многочлен. Урок математики 7 класс
Многочлен. Урок математики 7 класс Неклассические логики. (Глава 6)
Неклассические логики. (Глава 6) Решение иррациональных уравнений и их систем
Решение иррациональных уравнений и их систем Рассмотрение свойств биссектрис параллелограмма. Задачи
Рассмотрение свойств биссектрис параллелограмма. Задачи Презентация Финансовые вычисления по простым и сложным процентам
Презентация Финансовые вычисления по простым и сложным процентам Предел функции. Непрерывность функций одной переменной
Предел функции. Непрерывность функций одной переменной Презентация по математике "Как математику преподавать, чтоб математиками стать" - скачать
Презентация по математике "Как математику преподавать, чтоб математиками стать" - скачать  Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса
Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса Теорема Пифагора
Теорема Пифагора Весёлые клоуны. «Интерактивная мозаика»
Весёлые клоуны. «Интерактивная мозаика» Кластерный анализ. Практическое занятие №3
Кластерный анализ. Практическое занятие №3 Математический язык. 7 класс
Математический язык. 7 класс Игра–тренажёр. На лесной полянке. Математика 1 - 2 класс
Игра–тренажёр. На лесной полянке. Математика 1 - 2 класс Решение задач с помощью дробно-рациональных уравнений
Решение задач с помощью дробно-рациональных уравнений Решение заданий 6. ЕГЭ 2017. Математика, И.В. Ященко. 36 вариантов
Решение заданий 6. ЕГЭ 2017. Математика, И.В. Ященко. 36 вариантов Преобразование тригонометрических графиков
Преобразование тригонометрических графиков Подобие треугольников
Подобие треугольников