Содержание
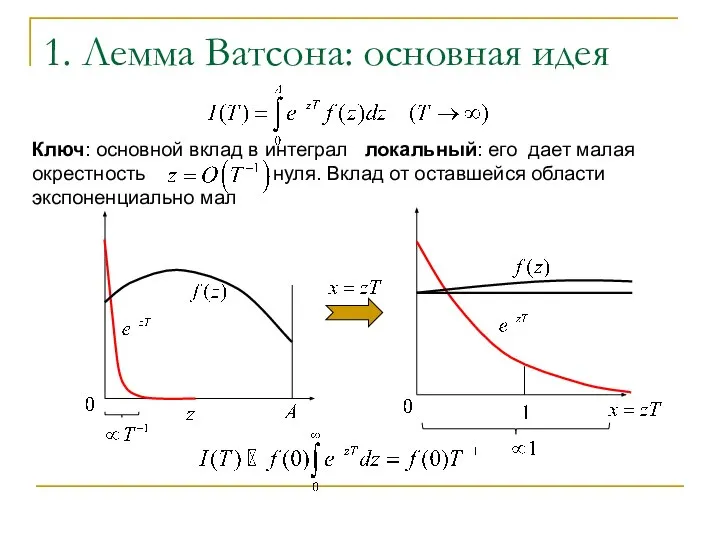
- 2. 1. Лемма Ватсона: основная идея Ключ: основной вклад в интеграл локальный: его дает малая окрестность нуля.
- 3. 2. Лемма Ватсона: пример Т.к. основной вклад в интеграл приходит из малой окрестности точки t=0 естественно
- 4. 3 Лемма Ватсона: окончательная формулировка Лемма Ватсона (общий случай) Используется тот факт, что
- 5. Способ 2 : раскладываем и пользуемся леммой Ватсона 4. Пример Способ 1 : интегрирование по частям
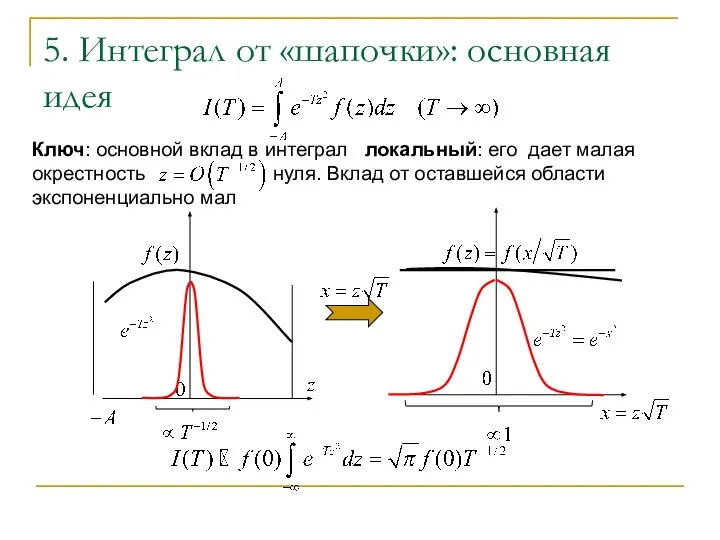
- 6. 5. Интеграл от «шапочки»: основная идея Ключ: основной вклад в интеграл локальный: его дает малая окрестность
- 7. 6. Интеграл от «шапочки»: вычисления
- 8. 7. Обобщение: Метод Лапласа Пусть Тогда основной вклад в интеграл дает малая окрестность точки
- 9. 8. Пример. Формула Стирлинга Относительная погрешность Представленный пример является обобщением стандартного метода Лапласа: здесь точка минимума
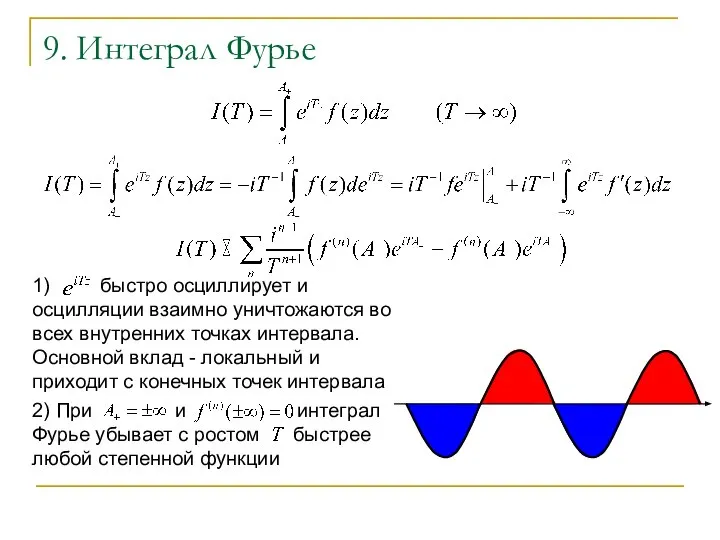
- 10. 9. Интеграл Фурье 1) быстро осциллирует и осцилляции взаимно уничтожаются во всех внутренних точках интервала. Основной
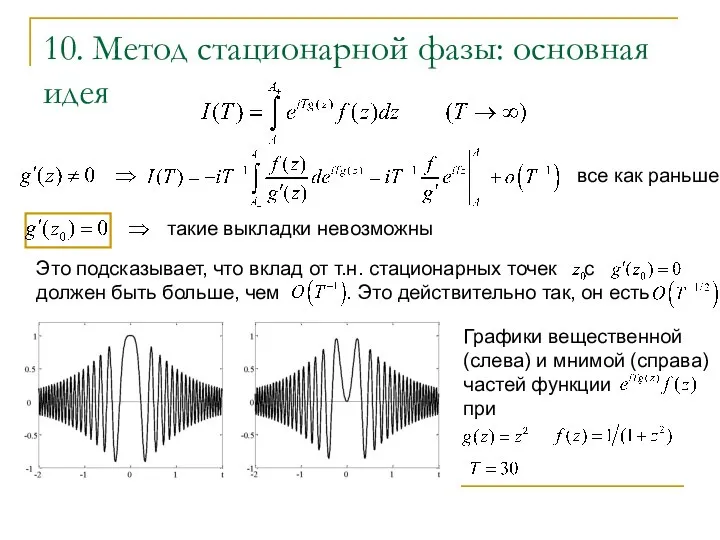
- 11. 10. Метод стационарной фазы: основная идея Графики вещественной (слева) и мнимой (справа) частей функции при все
- 12. 11. Метод стационарной фазы: вычисления Знак совпадает со знаком
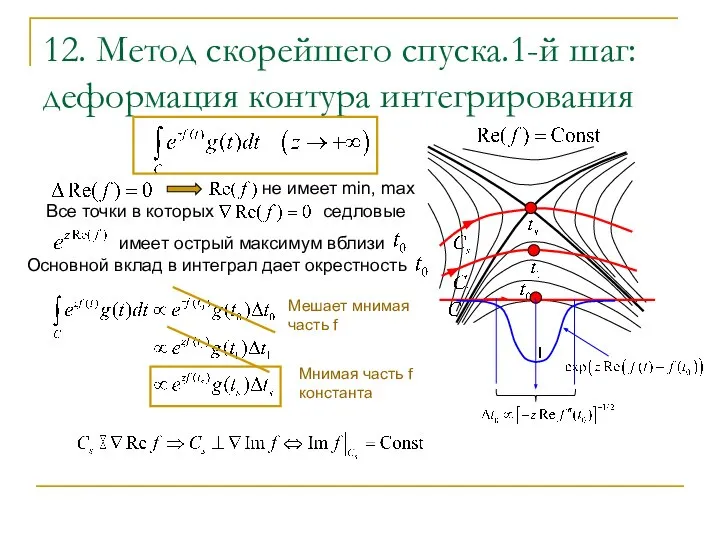
- 13. 12. Метод скорейшего спуска.1-й шаг: деформация контура интегрирования Мешает мнимая часть f Мнимая часть f константа
- 14. 13. Метод скорейшего спуска.2-й шаг: локальный анализ Вдоль выбранного пути интегрирования Перенормировка
- 15. 14. Метод скорейшего спуска: резюме Не меняя значения интеграла так изменяем контур интегрирования, чтобы он проходил
- 16. 15. Пример: функция Эйри Контур С, начинается на бесконечности с и заканчивается на бесконечности с Линии
- 17. 16. Пример: функция Эйри Перенормировка g(x,t) в новых переменных
- 19. Скачать презентацию











 Тренажёр. Таблица умножения. «Юные водители»
Тренажёр. Таблица умножения. «Юные водители» Кроссворд по геометрии, 7 класс
Кроссворд по геометрии, 7 класс Формула полной вероятности
Формула полной вероятности Презентация по математике "Платоновы тела – ключ к устройству Земли и Мироздания" - скачать
Презентация по математике "Платоновы тела – ключ к устройству Земли и Мироздания" - скачать  Математика 5 класс. Вычитание
Математика 5 класс. Вычитание Тригонометричні рівняння
Тригонометричні рівняння Числа 1-5. Состав числа
Числа 1-5. Состав числа Физика волновых явлений. (Лекция 1)
Физика волновых явлений. (Лекция 1) Некоторые другие приемы сравнения дробей
Некоторые другие приемы сравнения дробей Измерение углов
Измерение углов Дидактический материал по математике. Словарные диктанты для 5 – 6 классов
Дидактический материал по математике. Словарные диктанты для 5 – 6 классов ЕГЭ 2016. Базовый уровень
ЕГЭ 2016. Базовый уровень Презентация по математике "Дизъюнктивные нормальные формы (ДНФ). Совершенные дизъюнктивные нормальные формы (СДНФ)" - скачать
Презентация по математике "Дизъюнктивные нормальные формы (ДНФ). Совершенные дизъюнктивные нормальные формы (СДНФ)" - скачать  Применение презентаций на уроках математики как один из способов повышения интереса к учебе
Применение презентаций на уроках математики как один из способов повышения интереса к учебе Операции над множествами
Операции над множествами Делимость целых чисел
Делимость целых чисел Приведение дробей к общему знаменателю и их сравнение. Сравнение дробей с единицей
Приведение дробей к общему знаменателю и их сравнение. Сравнение дробей с единицей Уравнение плоскости по трем точкам с использованием матриц
Уравнение плоскости по трем точкам с использованием матриц Презентация по математике "Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры" - скачать
Презентация по математике "Занимательно о математике. Древняя нумерация, старинные меры длины, интересные цифры" - скачать  Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Математика. 2 класс. Тема: «Закрепление изученного материала.»
Математика. 2 класс. Тема: «Закрепление изученного материала.»  Стереометрия. Многогранники
Стереометрия. Многогранники Зигзаг удачи. Городская математическая игра
Зигзаг удачи. Городская математическая игра Пирамида. Многогранник, составленный из многоугольника
Пирамида. Многогранник, составленный из многоугольника Построение графика функции
Построение графика функции Предмет математической статистики
Предмет математической статистики Математические предложения
Математические предложения